ABSTRACT
Motivation In recent years, the well-known Infinite Sites Assumption (ISA) has been a fundamental feature of computational methods devised for reconstructing tumor phylogeny trees and inferring cancer progression. However, recent studies leveraging Single Cell Sequencing (SCS) techniques showed evidence of a number of recurrence and mutational loss in several tumor samples, an observation which essentially violates a strict ISA (e.g. [17].)
Results We present the SASC (Simulated Annealing Single Cell inference) tool, a new model and a robust framework based on Simulated Annealing for the inference of cancer progression from the SCS data.
Our main objective is to overcome the limitations of the Infinite Sites Assumption by introducing a version of the Dollo parsimony model which indeed allows the deletion of mutations from the evolutionary history of the tumor. We demonstrate that SASC achieves high levels of accuracy when tested on both simulated and real data sets and in comparison with other available methods.
Availability The Simulated Annealing Single Cell inference tool (SASC) is open source and available at https://github.com/sciccolella/sasc.
Contact s.ciccolella{at}campus.unimib.it
1 INTRODUCTION
Recent developments of targeted therapies for cancer patients rely on the accurate inference of clonal evolution and progression of the particular cancer. As discussed in several recent studies such as [22] and [32], understanding the order of accumulation and prevalence of somatic mutations during cancer progression can help better devise therapeutic strategies.
Most of the available techniques for infereing cancer progression rely on data from next-generation bulk sequencing experiments where only a proportion of observable mutations from a large amount of cells is obtained, without the distinction of the cells that carry them. In recent years, many computational approaches have been developed for the analysis of bulk-sequencing data with the purpose of inferring tumoral subclonal decomposition and reconstructing tumor phylogenies [31, 14, 12, 33, 23, 20, 7, 21, 30, 3].
Single Cell Sequencing (SCS) promises to deliver the best resolution for understanding the underlying causes of cancer progression. However, it is still difficult and expensive to perform SCS experiments with a good degree of confidence or robustness. The techniques available nowadays are producing datasets which contain a high amount of noise that include allelic dropout (false negatives) and missing values, due to lack of read coverage and false positive calls – even in a relatively small fraction. Although this sequencing technology is rapidly improving, and some issues such as the presence of doublets are slowly fading away, it is important to develop methods that are able to infer cancer progression despite the lack of accuracy in the data produced by current SCS techniques.
Various methods have been developed for this purpose [13, 27, 34], some of them introducing a hybrid approach of combining both SCS and VAF data [25, 19, 29]. Most of these methods, however, rely on the Infinite Sites Assumption (ISA), which states that a mutation is acquired at most once in the tree and is never lost. The ISA was introduced in [15] by Kimura in 1969: one of the pioneering papers of the neutral model of the evolution of species. This simplifying assumption also leads to a computationally tractable model of evolution [11] – something that is safe to make in this setting. Cancer progression, however, is a very fast and aggressive form of evolution with limited data supporting neutral evolution [5], but rather there is evidence of selection [2, 5] – something that is particularly true in tumour samples after a relapse [18, 10, 5], where the tumour has already been highly selected by the therapy targeted to destroy it. Thus, one would be expect that we must abandon the strict Infinite Sites Assumption in this setting, and indeed this is the case, as more and more recent studies are demonstrating that the ISA does not always hold [17, 4, 2]. In [4], the authors find that large deletions on several branches of a tree can span a shared locus, and thus a given mutation may be deleted independently multiple times. In [2], the authors show that in certain cases, homozygous deletions in cancer genomes can even provide a selective growth advantage. Each (independent) deletion of an acquired mutation takes us further away from the ISA. Some recent methods such as TRalT [25] and SiFit [34] permit violations of the ISA, in particular they allow deletions of mutations without specifying a particular model of evolution. While this is a start, there is a need to develop more general methods, based on a relaxation to the ISA – something that is not robust to even a single back-mutation.
Example of a binary matrix that does not allow a Perfect Phylogeny, since columns a and b are in conflict, i.e. the four gametes rule [11] doesn’t hold. The tree represents one of the possible Dollo Phylogenies that explain the matrix.
The Dollo model [26] is designed exactly for cases where stricter models like the one based on the ISA may not provide a solution. In particular, while it still constrains that a mutation can only be acquired once, it allows any number of independent losses of the mutation – a model that is very pertinent in light of the above cases [17, 4, 2] for the ISA not holding. Of course, the Dollo model does not have the convenient computational tractability of [11]. However, if we restrict the number of losses of any mutation to 1 or 2 (rather than strictly 0), the resulting-solution search space is still small enough for practical purposes.
Here we propose the Simulated Annealing Single Cell inference tool (SASC) a maximum likelihood tree search framework that allows violations of the ISA, in the form of mutation deletions, by incorporating the Dollo parsimony model [8].
2 FORMULATION OF THE TREE RECONSTRUCTION PROBLEM
As mentioned before, cancer progression reconstruction can be modeled as a character-based phylogeny reconstruction problem in which mutations are represented by the presence/absence of characters in different cell groups represented by the species.
We model the input as an n × m ternary matrix Iij, where an entry Iij = 0 indicates that the sequence of cell i does not have mutation j, Iij=1 indicates the presence of mutation j in the sequence of the cell i, and a 2 indicates that there is no enough information about the presence/absence of the mutation j in the cell i. Uncertainty about the presence of a mutation in acell is a consequence of insufficient coverage in the sequencing.
However, uncertainty is not the only issue in the sequencing process: false positives/negatives are present in the entries of the input. We assume that these errors occurs equidistributed and independent across all the (known) entries of the matrix I. Namely,if Eij denotes the estimated n×m output matrix, α denotes the false negative rate and β denotes the false positive rate; then for each ij entry of E it holds:
P(Iij = 0 |Eij = 0) = 1 − β
P(Iij = 1 |Eij = 0) = β
P(Iij = 1 |Eij = 1) = 1 − α
P(Iij = 0 |Eij = 1) = α
We aim to find a matrix E that maximizes the following function

Example of two Dollo phylogeny trees that explain the same binary matrix. It is important to notice that ancestry order of mutations a and c is inverted and different deletions can equally explain the matrix.
In other words, we attempt to maximizes the likelihood of the observed matrix I [13]. We stress the fact that the values of the unknown entries of the input matrix do not intervene in the objective function. Thus, P(Iij = 2 |Eij = 1) = P(Iij = 2 |Eij = 0) = 1.
Moreover, since we are interested in the evolutionary history reconstruction of the input cells we must provide, together with matrix E, an phylogenetic tree which explain the evolution of the mutations present in the cells of the output matrix.
A phylogeny tree is defined as a rooted labeled tree T in which the label set corresponds to a set of character and leaves of T have the void label. The state of a node is defined as the set of labels (characters) in the path from the root. The state of each leaf l of T admits a natural representation by a m-dimensional binary vector, that we denote by D(T,l), such that D(T,l)j = 1 if and only if the character j is in the state of l and zero otherwise.
We said that the tree T encodes a matrix E if it exists a mapping σ of the rows (species) of E to the leaves of T such that for every row Ei = D(T, σi) where σi denotes the image of row i by σ.
We can express the likelihood of the matrix E as: 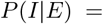
 . Since the involved probabilities are in [0,1] it is convenient to move to a (linear) log-likelihood maximization objective function of the form:
. Since the involved probabilities are in [0,1] it is convenient to move to a (linear) log-likelihood maximization objective function of the form:

2.1 Introduction of Dollo(k) model
The Dollo parsimony rule can be interpreted as the impossibility of having an identical mutation in the evolutionary trajectory. This rule can be translated in the phylogeny tree model as the presence of at most one introduction of any single mutation but a non bounded number of mutational deletions.
From an algorithmical point of view the phylogeny reconstruction model with a Dollo evolutionary model is a NP-complete problem [1, 6]. A hierarchical chain of restricted versions of the model can be obtained by bounding the number of deletion for each character. We denote as Dollo(k) the evolutionary model in which each mutation can be acquire only once and can be lost at most k times. In this way Dollo(0) and Dollo(1) correspond to the perfect an persistent phylogeny model respectively. In the tree generation process for the Dollo(k) model (k > 0) we are required to augment the phylogenic tree T representing the cancer progression by adding nodes that represent the loss of a mutation, i.e. a node labelled  , representing the l-th loss of mutation p. As a consequence, the function D(T, σ) needs to be slightly modified to take account of the losses. The genotype profile of a row i is then given by the mutations acquired in the path from root to the parent of σi minus all the potential losses encountered in the path. We stress the fact that, when deletions are introduced, the set of feasible phylogenies that represent a given solution is no longer unique as in the case of Perfect Phylogeny. We can see that switching the label of nodes b−; and d− in Figure 1 produces a different tree that is still a solution of the proposed input matrix. Moreover we see that ancestor relation between characters is different in both representations. When the number of cells, mutations and possible deletions increases and with the noise caused by false calls and missing entries this problem is greatly amplified and it will become possible that numerous cancer progression could equally explain the same input. A more complex example can be seen in Figure 2 where a different order of mutations and a different set of deletions can equally explain a given input.
, representing the l-th loss of mutation p. As a consequence, the function D(T, σ) needs to be slightly modified to take account of the losses. The genotype profile of a row i is then given by the mutations acquired in the path from root to the parent of σi minus all the potential losses encountered in the path. We stress the fact that, when deletions are introduced, the set of feasible phylogenies that represent a given solution is no longer unique as in the case of Perfect Phylogeny. We can see that switching the label of nodes b−; and d− in Figure 1 produces a different tree that is still a solution of the proposed input matrix. Moreover we see that ancestor relation between characters is different in both representations. When the number of cells, mutations and possible deletions increases and with the noise caused by false calls and missing entries this problem is greatly amplified and it will become possible that numerous cancer progression could equally explain the same input. A more complex example can be seen in Figure 2 where a different order of mutations and a different set of deletions can equally explain a given input.
2.2 Simulated Annealing approach
Unlike the Perfect case, the Dollo(k)-phylogeny reconstruction problem is NP-complete [1, 6]. In this section we describe a Simulated Annealing [16] approach in order to find a tree which maximizes the likelihood of an incomplete input matrix and that satisfies the Dollo(k) phylogeny model.
Simulated annealing is a meta-heuristic which explore the solution by a random walk on the (discrete) feasible space. The space topology, that is the way in which states are connected is part of the algorithm construction. At each the step, the probability of moving to some neighbouring state with a better value change according to a parameter called the temperature that continuously decreases.
In the first part of the algorithm execution temperature has a big value and it is possible accept to move into a state with a worse objective value, but as temperature decreases, acceptance probabilities converge to values for which the algorithm moves only to a local optimum.
Thus, a key element of the algorithm is the construction of the neighborhood of each feasible candidate since it regulates the way in which the feasible space is explored.
2.2.1 Neighborhood operation
We developed a two-phased algorithm: in the first phase the goal of the algorithm is to find a maximum likelihood Perfect Phylogeny tree, while in the second phase deletions are added in order to improve the solution by inducing a Dollo(k) model.
In the following we describe for each phase the considered neighbourhood of each state which defines the set of possible simulated annealing moves for each phase. We will denote by ρ(i) the parent of i according to the actual tree state. Moreover, we set probability acceptance as min{exp(Δv/T), 1} where Δv is the possible improvement on the problem value and T is the temperature which decrease according to a geometric (cooling) factor equals 10−5.
In the First Phase SASC searches for the max likelihood Perfect Phylogeny tree by moving subtrees with an operation that is close to the Prune and Regraft operation: given two nodes u, v ∈ T such that neither is an ancestor of the other, we can move to a neighbour tree as follows: The subtree rooted in v is pruned, i.e. it is detached from ρ(v), and it is grafted as a new child of u, meaning that a new edge (v, u) is added, while the edge (ρ(v), v) is deleted.
The goal of the Second Phase of the algorithm is to extends the found solution by adding possible losses and therefore searching the maximum likelihood in a bigger region by finding a Dollo(k) solution. In this phase is not possible to modify the overall structure of the tree T, however it is possible to add nodes representing solutions, delete them and swapping the labels of two nodes. The following moves are introduced:
Add a deletion: Given a node u ∈ T and a mutation z of u, we add the deletion of a mutation whose an ancestor of u as its parent. The node z−, representing the loss of the mutation z, is created. The edge (u, ρ(u)) is split into two and z−is the new middle node.
Remove a deletion: given a node u ∈ T labelled as a loss is removed from the tree T, i.e. all children of u are added as children of p(u), then u is deleted.
Swap nodes labels: given two randomly chosen nodes u, v ∈ T the labels of u and v as swapped. The rationale behind this option is to change the order of mutations that could have mistakenly placed in the previous phase due to the limitation of the ISA. If a previously added deletion becomes invalid due to this operation, e.g. the lost mutation is not acquired in the path from the root to u, then the mutation loss in question is deleted from the tree T.
In both phases, a reassignment of the cells to the tree leaves can take place. This move is performed according to the change a cell assignment operation: given a cell i its image in the tree is chosen uniformly random in the set of the nodes of the tree. This assignment is equivalent to changing the parent of a leaf, since σ denotes the leaves of the tree.
3 RESULTS
3.1 Results on real cancer data
We tested SASC on Childhood Acute Lymphoblastic Leukemia data from [9]. In particular we focused on Patient 4 and Patient 5 of this study. Patient 4 consists of 78 somatic mutations over 143 cells, while Patient 5 is affected by 104 SNV over 96 cells. The original study estimated an allelic drop-out rate of less than 30%. Since the trees in [9] are manually curated and of high quality, we select them as the ground truth.
Tree inferred by SASC for Patient 4 of Childhood Lymphoblastic Leukemia data from [9]. Different clones are indicated with different colors while the red-colored nodes indicate a deletion of mutations, while mutation highlighted in bold are the mutations indicated as driver in the original sequencing study. Mutations in bold and colored are driver mutations for the same colored clone.
To ensure the absence of doublets we pre-processed the input using the Single Cell Genotyper (SCG) tool [28]. SCG is a statistical model which removes all cells of the datasets that are likely to be doublets. Since SCG is reliable, we focus on doublets-free data in the design and experimental analysis of SASC. Moreover, doublets are becoming rarer as single cell technology progresses.
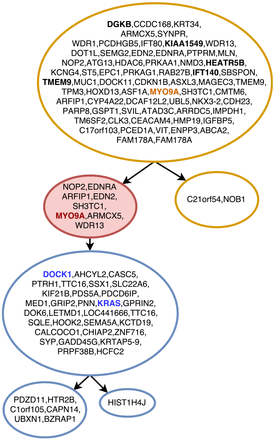
Figure 3 shows the tree inferred by SASC for Patient 4; SASC correctly infers the tree structure assumed in the study as well as the number of subclonal population. The driver mutations are correctly identified, and mutations COL5A2, SDPR and TRHR are inferred as deletions. Furthermore bolded and colored mutations indicate the correctly inferred specific driver mutations for the subclone of the same color; it is interesting to notice that the violet clone is supposed to not have mutation COL5A2 and this particular mutation is indeed deleted in the clone. This solution was found assuming a Dollo(2) phylogeny model with no restriction on the total number of deletions in the cancer progression.
In Figure 4, the inferred solution for Patient 5 of the same study is shown; as in the previous dataset, our inferred tree perfectly supports the hypotheses proposed in the sequencing study. In fact it correctly infers the topology of the tree, as well as the driver mutations. Boldfaced mutations are the driver mutations for the tree or the subclone with the same color. This solution was found assuming a Dollo(2) phylogeny model with a total restriction of 10 deletions in the cancer progression.!
We also tested SASC on a recent Single-cell RNA-seq sequencing study of primary Breast Cancer [16]. Figure 6 represents the inferred cancer progression of Patient 9 of the study. Raw TPM values from the study were publicly available on the NCBI Gene Expression Omnibus database, we used a threshold of 10000 TPM to detect a total of 42 mutations for the 60 available cells sequenced for Patient 9. The sequencing study does not propose a clonal tree, however several deletions were expected, since it is typical of genetic alterations in breast cancer. We ran SASC with two different configurations: first we did not limit the number of mutations under a Dollo(2) model and it inferred a total of 20 deletions. Then, for a clearer visualization (represented in Figure 6) we allowed only 5 deletions. Furthermore B2M, which is considered a driver mutation [24], is correctly inferred as the first occurred mutation.
3.2 Results on simulated data and comparison with other approaches
We have also tested our method on simulated data, where the ground truth is known. Still, we recall that it is possible that a completely different tree achieves a better likelihood than the one obtained via simulation. This problem is essentially unavoidable, since generating a progression that is the unique solution for the corresponding SCS input matrix requires adding artifacts to both the tree and the matrix. It is unlikely that the resulting instance would satisfy even the basic assumptions on cancer progression.
Tree inferred by SASC for Patient 5 of Childhood Lymphoblastic Leukemia data from [9]. Different clones are indicated with different colors while the red-colored nodes indicate a deletion of mutations, while mutation highlighted in bold are the mutations indicated as driver in the original sequencing study. Mutations in bold and colored are driver mutations for the same colored clone.
Parameters used to simulate the input matrice, where k is the maximum number of allowed mutation deletions, α is the false negative ratio, β the false positive ratio, and γ is the missing data ratio
3.2.1 Generation of Simulated datasets
We randomly generated 50 clonal trees for each combinations of the parameters listed in Table 1. Given a fixed number of subclones S we generated a random tree of S nodes by adding a new node as a child of a random pre-existing one. Each of the M mutations q1,…, qM is then randomly assigned to one of the si subclones with uniform distribution. We allowed at most a fixed number of k deletions in each clonal tree: therefore k new nodes are added to the tree at random positions. A deletion of a mutation is then assigned to each of the k new nodes, by picking at random, with uniform distribution, one of the mutations affecting the parent of the node and that has not been already chosen as a deletion.
To obtain the genotype profile of the n cells, we randomly assigned each cell to a node and derived its profile from the clonal tree (independently with repetition and with uniform distribution). Finally to simulate noise on the data, we flipped a 0 entry to 1 with probability β to simulate false positives and a 1 entry to 0 with probability α to simulate false negatives. Moreover each entry has a γ probability to be a missing entry. All errors and missing values are uniformly and independently distributed, without repetitions. We simulated 2 datasets, based on the parameters in Table 1.
3.2.2 Evaluation on simulated datasets
We measured the accuracy of SASC with two standard cancer progressions measures used in various studies [19, 13] and a novel approach to test the quality of subclonal inference, defined as follows:
Ancestor-Descendant accuracy: This measure considers all pairs of mutations (x,y) that are in an ancestor-descendant relationship in the ground truth tree T. For each such pair we check whether the ancestor-descendant relationship is conserved in the inferred tree I. The score is defined by the ratio of the preserved relationships in I over the total number of relationships in T.
Different-Lineage accuracy: Similar to the previous measure, it considers all pairs of mutations (x, y) that are not in an ancestor-descendant relationship, i.e. are in different branches of T. The score is given by the ration of the preserved relationship in I over the total number of relationships in T.
Subclones accuracy: This new accuracy score checks whether the subclones in T are correctly preserved in I. Let us define a boolean function Ca(x, y) that is equal to true (t) if and only if mutations x and y are acquired in the same subclone in the tree a, false (f) otherwise. Let be TP, FP and FN the number of true positives, false positives and false negatives respectively, that is TP (FP, FN respectively) is the number of pairs (x, y) such that CI(x, y) = t ^ CT(x, y) = t (CI(x, y) = f ^ CT(x, y) = t, ^ CI(x, y) = t ^ CT(x, y) = f respectively). The standard definition of precision
 and recall
and recall  applies. Moreover the overall score of the accuracy is given by the F1 score:
applies. Moreover the overall score of the accuracy is given by the F1 score: 
Accuracy results for Experiment 1, described in Section 3.2.1. SASC and SCITE are relatively close in accuracy for all the measures. The two lower plots show the values of standard precision and recall measures for the ISA violations called by SASC. It is important to consider that all the accuracy measures used ignore deletions.
Note that none of previous metrics account for ISA violations. We decided to compare SASC against SCITE [13]: while B-SCITE [19] is a clear improvement over SCITE, it combines single cell data with bulk sequencing data — since we do not manage the latter kind of data, a fair comparison is not feasible. OncoNEM [27] and SiFit [34] were excluded because they infer cell lineage progressions instead of mutational progression, therefore it is not possible to compare our predictions with theirs.
Figures 5 and 7 show the comparison of accuracy between SASC and SCITE; in average both the methods scores relatively close to each other obtaining good results in both the experiments. As already stated none of the accuracy measures consider the presence of deletions, therefore methods that infer Perfect Phylogenies are not penalized by these accuracy measures, even if they infer the wrong evolutionary model.
4 DISCUSSION
SASC is an accurate tool for inferring intra-tumor progression and subclonal composition from SCS data and it is robust to various degrees of noise in the dataset. While SASC is highly accurate on simulated data, it cannot outperform SCITE on those simulated data. At the same time, the currently available quality measures are biased against mutation losses, therefore a more complete comparison is necessary before drawing definitive conclusions. It is indeed an open work to develop a measure that takes deletions into account.
Tree inferred by SASC for Patient 9 of primary Breast Cancer data from [16]. Red-colored nodes indicate a deletion of mutations, while mutation highlighted in bold are the mutations indicated as driver.
On real data, SASC performs extremely well and it infers correctly the expected phylogeny tree structures, as well as the driver mutations and the decomposition of the clones. Furthermore, it can be used on very large datasets. Since the actual value of the parameters α and β are unknown, we suggest to try different prior values for α and β: they affect the overall solution and can lead to different sets of solutions. A particularly interesting example is given by the inferred tree in Figure 4. The corresponding input dataset in this case contains more than 5000 conflicts between characters ‒ according to the four gametes rule, each one witnessing a violation of the ISA, by definition. With only a slight relaxation of the infinite sites assumption — the Dollo(2) model — SASC is able to infer an accurate solution with a total of 10 deletions, while Perfect Phylogeny methods would require a large amount of flips on the entries just to produce a feasible solution. A performance measure that takes deletion into account would likely give a better outcome for SASC.
In summary, SASC provides new insights to the analysis of intratumor heterogeneity by proposing a new progression model that has never been previously applied in cancer phylogeny reconstruction on Single Cell data.
Accuracy results for Experiment 2, described in Section 3.2.1. SASC and SCITE are relatively close in accuracy for all the measures. The two lower plots show the values of standard precision and recall measures for the ISA violations called by SASC It is important to consider that all the accuracy measures used ignore deletions.
Funding
This work was also supported by start up funds (Weill Cornell Medicine) to IH.
ACKNOWLEDGEMENT
SC acknowledges a Mobility Exchange Fellowship from University of Study Milan-Bicocca. Part of this work has been done during SC visit at Weill Cornell.