Joint angle variability in 3D bimanual pointing: uncontrolled manifold analysis

Abstract

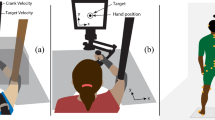
The structure of joint angle variability and its changes with practice were investigated using the uncontrolled manifold (UCM) computational approach. Subjects performed fast and accurate bimanual pointing movements in 3D space, trying to match the tip of a pointer, held in the right hand, with the tip of one of three different targets, held in the left hand during a pre-test, several practice sessions and a post-test. The prediction of the UCM approach about the structuring of joint angle variance for selective stabilization of important task variables was tested with respect to selective stabilization of time series of the vectorial distance between the pointer and aimed target tips (bimanual control hypothesis) and with respect to selective stabilization of the endpoint trajectory of each arm (unimanual control hypothesis). The components of the total joint angle variance not affecting (V_COMP) and affecting (V_UN) the value of a selected task variable were computed for each 10% of the normalized movement time. The ratio of these two components R_V=V_COMP/V_UN served as a quantitative index of selective stabilization. Both the bimanual and unimanual control hypotheses were supported, however the R_V values for the bimanual hypothesis were significantly higher than those for the unimanual hypothesis applied to the left and right arm both prior to and after practice. This suggests that the CNS stabilizes the relative trajectory of one endpoint with respect to the other more than it stabilizes the trajectories of each of the endpoints in the external space. Practice-associated improvement in both movement speed and accuracy was accompanied by counter-intuitive lack of changes in R_V. Both V_COMP and V_UN variance components decreased such that their ratio remained constant prior to and after practice. We conclude that the UCM approach offers a unique and under-explored opportunity to track changes in the organization of multi-effector systems with practice and allows quantitative assessment of the degree of stabilization of selected performance variables.

Appendix

Computation of variance within the uncontrolled manifold and within the orthogonal manifold

A selected task variable defines an uncontrolled manifold (UCM) in the appropriate joint space. Here we describe how the studied task variables define the corresponding UCMs at each percentage of movement time. Let M denote the mean joint configuration across trials. Let r ₀ be the value of the task variable for the mean joint configuration and r _k the value of the task variable for the kth trial. If the joint configuration vector (A _k ) of a particular trial remains in the vicinity of M, then the deviation of the task variable Δr _k =r _k −r ₀ relates to the deviation of joint-configuration Δk=M−A _k approximately as:

$$ {\mathbf{\Delta r}}_{\mathbf{k}} = {\mathbf{J}}{\text{*}}{\mathbf{\Delta k}} $$

(1)

where J is a Jacobian matrix. Its elements are the partial derivatives of the coordinates of the task variable with respect to the joint angles in the mean joint configuration. The nullspace of J represents those changes of joint configurations that do not cause any change in the task variable. The UCM is defined by this nullspace and spanned by m independent vectors (e1,...,em) at each instant of time. If DV is the dimension of the task variable and DF is the number of degrees of freedom of the multi-joint system, then m=DF−DV (Scholz et al. 2000).The component of Δk, which lies in the UCM, is obtained by its projection on to the nullspace. Let us denote this projection as Δk^UCM:

$$ {\mathbf{\Delta k}}^{{\text{UCM}}} = \sum\limits_{i = 1}^m {\left\langle {{\mathbf{\Delta k}},\;{\mathbf{ei}}} \right\rangle } * {\mathbf{ei}} $$

(2)

where < > denotes scalar product.

The component that is orthogonal to the null space is defined as:

$$ {\mathbf{\Delta k}}^{{\text{ORT}}} = {\mathbf{\Delta k}} - {\mathbf{\Delta k}}^{{\text{UCM}}} $$

(3)

We computed the variances per DF of both components of the joint configuration vectors across N trials. The variance of the component, which lies within the UCM, is defined as compensated variance V_COMP:

$$ {\text{V}}_{{\text{COMP}}} = \sum\limits_{k = 1}^N {\left( {{\mathbf{\Delta k}}^{{\text{UCM}}} } \right)} ^{\text{2}} {\text{/}}\left( {\left( {{\text{DF}} - {\text{DV}}} \right) * {\text{N}}} \right) $$

(4)

The variance per DF of the orthogonal component is defined as uncompensated variance V_UN:

$$ {\text{V}}_{{\text{UN}}} = \sum\limits_{k = 1}^N {\left( {{\mathbf{\Delta k}}^{{\text{ORT}}} } \right)} ^{\text{2}} {\text{/}}\left( {{\text{DV}} * {\text{N}}} \right) $$

(5)

We computed the Jacobians for the described bimanual task variable and for the unimanual task variables for each arm separately. Numerical derivation was applied for this computation.

Bimanual control hypothesis

The hypothesized task variable for the bimanual control hypothesis is the vectorial distance between the pointer tip (Px, Py, Pz) and aimed target tip (Tx, Ty, Tz). The vectorial distance is denoted by R=(Rx, Ry, Rz)=(Tx, Ty, Tz)−(Px, Py, Pz).

Forward kinematics was used to compute R from given joint angles, thus the coordinates of R were given as functions of 14 joint angles. The angles 1 to 7 relate to the left arm, the angles 8 to 14 relate to the right arm. The angles for the shoulder, elbow and wrist joints are described in the Methods. The joint angles (α1(t), α2(t), ..., α14(t)) and the associated vectorial distance as a function of the angles R(α1(t), ..., αj(t), ..., α14(t)) were given at each percentage of movement time (t=1, ..., 100).

Let Jxj(t), Jyj(t) and Jzj(t) be the partial derivatives of Rx, Ry and Rz with respect to αj for t=1, ..., 100.

For numerical derivation of the partial derivatives of R with respect to the joint angle αj we need to compute the value of R at the virtual joint configuration (α1(t), ..., αj(t-1), ..., α14(t)).

Note that (α1(t), ..., αj(t-1), ..., α14(t)) is a virtual joint configuration in which the jth joint angle is taken from the time bin that precedes the time bin when the other angles are considered.

Then the elements of the Jacobian are computed as the following:

$$\begin{array}{*{20}c} {{{\text{Jxj}}{\left( {\text{t}} \right)}={\left( {{\text{Rx(a1}}{\left( {\text{t}} \right)},...,{\text{aj}}{\left( {\text{t}} \right)},...,{\text{a14}}{\left( {\text{t}} \right)}} \right)} - {\text{Rx(a1}}{\left( {\text{t}} \right)},...,{\text{aj}}{\left( {{\text{t - 1}}} \right)},...,{\text{a14}}{\left( {\text{t}} \right)}{\text{)) / (aj}}{\left( {\text{t}} \right)} - {\text{aj}}{\left( {{\text{t - 1}}} \right)}{\text{)}}{\text{,}}}} \\ {{{\text{Jyj}}{\left( {\text{t}} \right)}={\left( {{\text{Ry(a1}}{\left( {\text{t}} \right)},...,{\text{aj}}{\left( {\text{t}} \right)},...,{\text{a14}}{\left( {\text{t}} \right)}} \right)} - {\text{Ry(a1}}{\left( {\text{t}} \right)},...,{\text{aj}}{\left( {{\text{t - 1}}} \right)},...,{\text{a14}}{\left( {\text{t}} \right)}{\text{)) / (aj}}{\left( {\text{t}} \right)} - {\text{aj}}{\left( {{\text{t - 1}}} \right)}{\text{)}}{\text{,}}}} \\ {{{\text{Jzj}}{\left( {\text{t}} \right)}={\left( {{\text{Rz(a1}}{\left( {\text{t}} \right)},...,{\text{aj}}{\left( {\text{t}} \right)},...,{\text{a14}}{\left( {\text{t}} \right)}} \right)} - {\text{Rz(a1}}{\left( {\text{t}} \right)},...,{\text{aj}}{\left( {{\text{t - 1}}} \right)},...,{\text{a14}}{\left( {\text{t}} \right)}{\text{)) / (aj}}{\left( {\text{t}} \right)} - {\text{aj}}{\left( {{\text{t - 1}}} \right)}{\text{)}}}} \\ \end{array} $$

The Jacobian is a matrix with 3 rows and 14 columns at each instant of time:

$$ {\mathbf{J}}\left( {\text{t}} \right) = \begin{array}{*{20}c} {{\text{Jx1}}\left( {\text{t}} \right){\text{,}}} & {{\text{Jx2}}\left( {\text{t}} \right),} & {...{\text{,}}} & {{\text{Jx14}}\left( {\text{t}} \right)} \\ {{\text{Jy1}}\left( {\text{t}} \right){\text{,}}} & {{\text{Jy2}}\left( {\text{t}} \right),} & {...{\text{,}}} & {{\text{Jy14}}\left( {\text{t}} \right)} \\ {{\text{Jz1}}\left( {\text{t}} \right){\text{,}}} & {{\text{Jz2}}\left( {\text{t}} \right),} & {...{\text{,}}} & {{\text{Jz14}}\left( {\text{t}} \right)} \\ \end{array} $$

The nullspace of J is 11-dimensional. The mean and the related deviation vectors were computed for the lower, middle and upper target separately. The variance within the UCM for the bimanual control hypothesis was also computed for each target separately using a particular form of Eq. (4) with DF=14 and DV=3:

$$ {\text{V}}_{{\text{COMP}}} = \sum\limits_{k = 1}^N {\left( {{\mathbf{\Delta k}}^{{\text{UCM}}} } \right)} ^{\text{2}} {\text{/}}\left( {11 * {\text{N}}} \right) $$

(6)

The variance within the orthogonal manifold was computed from Eq. (5):

$$ {\text{V}}_{{\text{UN}}} = \sum\limits_{k = 1}^N {\left( {{\mathbf{\Delta k}}^{{\text{ORT}}} } \right)} ^{\text{2}} {\text{/}}\left( {{\text{3}} * {\text{N}}} \right) $$

(7)

where N is the number of pointing movements (i.e. trials) to the aimed target.

Unimanual control hypothesis applied to the left and right arm

If two arms are considered separately, then the joint space for each arm is seven-dimensional. For the unimanual control hypothesis applied to the left arm the task variable is the position of the aimed target tip (Tx, Ty, Tz). For the unimanual control hypothesis applied to the right arm the task variable is the position of the pointer tip (Px, Py, Pz). Therefore, the corresponding UCMs for the left and right arm are approximated by the nullspaces of 3×7 matrices at each instant.

The elements of the Jacobian for the left and right arm are computed similarly to the computation of the Jacobian elements for the bimanual hypothesis, only using the task variables T and P instead of the vectorial distance R and seven angles of the corresponding arm instead of all 14 angles.

The nullspaces of the Jacobians for the left and right arm and thus, their UCMs are four-dimensional, while their ORTs are three-dimensional. The deviation vectors Δk _left and Δk _right are differences of the joint configuration of the left (α1_k, α2_k, ..., α7_k) or right arm (α8_k, α9_k, ..., α14_k) in the kth trial and the mean joint configuration of the left or right arm, respectively. The mean and the related deviation vectors were computed for the lower, middle and upper target separately. The variance per DF within the UCMs of the left and right arm can be obtained from Eq. (4) with DF=7 and DV=3, using Δk _left or Δk _right , respectively. The variance within the ORTs for the left and right arm can be computed from Eq. (5) with DV=3, using Δk _left or Δk _right , respectively.