Efficient Bayesian inference for COM-Poisson regression models

Abstract

COM-Poisson regression is an increasingly popular model for count data. Its main advantage is that it permits to model separately the mean and the variance of the counts, thus allowing the same covariate to affect in different ways the average level and the variability of the response variable. A key limiting factor to the use of the COM-Poisson distribution is the calculation of the normalisation constant: its accurate evaluation can be time-consuming and is not always feasible. We circumvent this problem, in the context of estimating a Bayesian COM-Poisson regression, by resorting to the exchange algorithm, an MCMC method applicable to situations where the sampling model (likelihood) can only be computed up to a normalisation constant. The algorithm requires to draw from the sampling model, which in the case of the COM-Poisson distribution can be done efficiently using rejection sampling. We illustrate the method and the benefits of using a Bayesian COM-Poisson regression model, through a simulation and two real-world data sets with different levels of dispersion.

1 Introduction

Observational and epidemiological studies often give rise to count data, representing the number of occurrences of an event within some region in space or period of time, e.g., number of goals in a football match, number of emergency hospital admissions during a night shift, etc. A standard approach to modelling count data is Poisson regression: the counts are assumed to be independent Poisson random variables, with means determined, through a link function (usually the $\log$), by a linear regression on available covariates. The Poisson model entails that the mean and variance are equal (equidispersion). However, count data frequently exhibit underdispersion or, especially, overdispersion (these are often just symptoms of model misspecification, e.g. omission of important covariates, presence of outliers, lack of independence, inadequate link function). In the presence of substantial overdispersion, a commonly used alternative to the Poisson regression model is the negative binomial regression model, which allows the variance to be larger than the mean.

This paper is concerned with an even more flexible model for count data, the COM-Poisson regression model (Sellers and Shmueli 2010; Guikema and Coffelt 2008), which allows the mean and the variance of count data to be modelled separately. The model is flexible enough to handle underdispersion, something that neither of the previous models can do. The COM-Poisson model has become more popular in recent years, with SAS/ETS (SAS Institute Inc 2014) software containing a frequentist implementation. The main factor which inhibits the more widespread use of COM-Poisson regression is that the normalisation constant of the COM-Poisson distribution does not have a closed form. We take advantage of an MCMC algorithm, known as the exchange algorithm (Møller et al. 2006; Murray et al. 2006), to estimate a Bayesian COM-Poisson regression model without computing any normalisation constant. The resulting improvements in computational speed and efficiency make the COM-Poisson regression model a viable and attractive alternative to the usual count data models.

The paper is organised as follows. In Sect. 2 we review the COM-Poisson distribution and regression model; show the drawbacks of its current implementation in R (R Core Team 2015) and SAS/ETS (SAS Institute Inc 2014) and then show how one can efficiently sample from the COM-Poisson distribution using rejection sampling. In Sect. 3 we show how to overcome the problem of an intractable likelihood in a Bayesian setting, using a data augmentation technique which requires sampling from the COM-Poisson distribution, and present an exact MCMC algorithm for the COM-Poisson regression model. We have focused on the Bayesian implementation of the COM-Poisson regression model which allows us to use prior information on the distribution of the regression coefficients. One can use different methods to estimate the normalisation constant (Geyer 1991) and apply the frequentist version of the regression model.

In Sect. 4 we apply the Poisson, negative binomial, and COM-Poisson regression models to one artificial and two real world data sets. The results indicate the inability of the first two models to correctly estimate the effect of the covariate on the response variable and show that the COM-Poisson regression model provides a better fit to the data. Finally, in Sect. 5 we compare the proposed MCMC algorithm with the one in Chanialidis et al. (2014) and show that the newly proposed MCMC samples from the correct posterior distribution and is computationally more efficient.

2 COM-Poisson distribution

The COM-Poisson distribution (Conway and Maxwell 1962) is a two-parameter generalisation of the Poisson distribution that allows for different levels of dispersion. We use a reparametrisation proposed by Guikema and Coffelt (2008): Y is said to have COM-Poisson($\mu ,\nu$) distribution if its probability mass function is

$$\begin{aligned} P(Y=y|\mu , \nu )=\left( \frac{\mu ^y}{y!}\right) ^\nu \frac{1}{Z(\mu , \nu )} \quad y=0, 1, 2, \ldots \end{aligned}$$

(1)

with $Z(\mu , \nu )=\displaystyle \sum \nolimits _{j=0}^{\infty }\left( \frac{\mu ^j}{j!}\right) ^\nu$ for $\mu >0$ and $\nu \ge 0$. The parameter $\nu$ governs the amount of dispersion: the Poisson distribution is recovered when $\nu =1$, while overdispersion corresponds to $\nu < 1$ and underdispersion to $\nu > 1$. The normalisation constant $Z(\mu , \nu )$ does not have a closed form (for $\nu \ne 1$) and has to be approximated, but can be lower and upper bounded. The original parametrisation of the COM-Poisson distribution can be obtained by replacing $\mu$ in (1) by $\lambda ^{\frac{1}{\nu }}$. More details on the COM-Poisson($\lambda$, $\nu$) parametrisation, and an asymptotic approximation of its normalisation constant are available in Minka et al. (2003) and Shmueli et al. (2005).

The mode of the COM-Poisson distribution is ${\lfloor \mu \rfloor }$, whereas the mean and variance of the distribution can be approximated by

$$\begin{aligned} \mathbb {E}[Y]\approx \mu + \frac{1}{2\nu }-\frac{1}{2}, \quad \quad \quad \mathbb {V}[Y]\approx \frac{\mu }{\nu }. \end{aligned}$$

(2)

Thus $\mu$ closely approximates the mean, unless $\mu$ or $\nu$ (or both) are small.

2.1 COM-Poisson regression

Sellers and Shmueli (2010) propose a COM-Poisson regression model based on the original $(\lambda ,\nu )$ formulation, whereas Guikema and Coffelt (2008) propose a COM-Poisson GLM based on the reparameterisation (1). We consider the following modification of Guikema and Coffelt (2008) model:

$$\begin{aligned}&P(Y_i=y_i|\mu _i, \nu _i)=\left( \frac{\mu _i^{y_i}}{y_i!}\right) ^{\nu _i}\frac{1}{Z(\mu _i, \nu _i)},\nonumber \\&\log {\mu _i}= \varvec{x}_i^\intercal \varvec{\beta } \quad \quad \Rightarrow \quad \mathbb {E}[Y_i]\approx \exp {\{ \varvec{x}_i^\intercal \varvec{\beta }\}},\nonumber \\&\log {\nu _i}= -\varvec{x}_i^\intercal \varvec{\delta } \quad \, \;\Rightarrow \quad \mathbb {V}[Y_i]\approx \exp {\{ \varvec{x}_i^\intercal \varvec{\beta } +\varvec{x}_i^\intercal \varvec{\delta }\}}, \end{aligned}$$

(3)

where Y is the dependent random variable being modelled, while $\varvec{\beta }$ and $\varvec{\delta }$ are the regression coefficients for the centring link function and the shape link function. The approximations on the mean and variance in (3) are accurate when $\mu$ and $\nu$ are not small (e.g., extreme overdispersion).

Both the likelihood and Bayesian approaches to the estimation of $(\mu , \nu )$ require the evaluation of the normalisation constant $Z(\mu , \nu )$. Note, in particular, that $Z(\mu ,\nu )$, unlike the normalisation constant of a posterior distribution, does not cancel out in a Metropolis-Hastings acceptance ratio. Possible solutions to this problem are:

• Truncation of the normalisation constant series.

• Use of the asymptotic approximation by Minka et al. (2003).

• Estimate upper and lower bounds for the value of the normalisation constant and use these in an MCMC algorithm (Chanialidis et al. 2014).

Only the latter is an exact method, albeit at a significant computational cost. The former two are approximations, the quality of which depends on the details of the implementation.

Deciding in which term one must truncate the normalisation constant is not simple since the “mass” of the normalisation constant depends on the values of $\mu$ and $\nu$. As an example, for an overdispersed distribution (with $\nu <1$), we will need to truncate at a higher term compared to an underdispersed distribution (with $\nu >1$). The R (R Core Team 2015) packages, compoisson (Dunn 2012) and COMPoissonReg (Sellers and Lotze 2015), provide functions to compute the probability mass by simply truncating the normalisation constant up to a specified precision. The latter package offers the ability to compute the associated COM-Poisson regression coefficients (in a maximum likelihood setting) only when the dispersion parameter $\nu$ is independent of the covariates. The COUNTREG procedure of the SAS/ETS (SAS Institute Inc 2014) software supports the COM-Poisson regression model (3), along with its original formulation by Sellers and Shmueli (2010). In order to deal with the problem of evaluating the normalisation constant $Z(\mu , \nu )$, the asymptotic approximation of Minka et al. (2003) is used for $\mu >20$, while the normalisation constant is computed using truncation for $\mu \le 20$ (when it is computationally easier). In this case, when one plots the probabilities of $Y=y$ across different values of $\mu$ (keeping the dispersion parameter $\nu$ constant), there exists a jump at $\mu =20$. Figure 1 shows this discontinuity of the probabilities for an overdispersed COM-Poisson distribution with $\nu =0.1$. The black line in each panel refers to the probability when computing the normalisation constant, while the red line refers to the probability when using the asymptotic approximation.

Fig. 1

Probabilities computed in SAS for different values of $\mu$. The black and red lines refer to the probabilities when computing the normalisation constant and when its asymptotic approximation is used. (Color figure online)

3 Bayesian methods for COM-Poisson regression models

The normalisation constant $Z(\mu , \nu )$ in the COM-Poisson distribution is not available in closed form, hence evaluating the likelihood can be computationally expensive. This makes it difficult to sample from the posterior distribution of the parameters in a COM-Poisson regression model. One possible solution is to use an asymptotic approximation of $Z(\mu , \nu )$ (Minka et al. 2003), which is known to be reasonably accurate when $\mu > 10$. Alternatively one could compute $Z(\mu , \nu )$ by truncating its series at the kth term, but in order to achieve reasonable accuracy k may need to be very large. Evaluation of $Z(\mu , \nu )$ could be avoided altogether using approximate Bayesian computation (ABC) methods. However, the resulting algorithms may not sample from the distribution of interest and are usually much less efficient than standard MCMC algorithms which assume that the normalisation constants are known or cheap to compute. We overcome the problem of having an intractable likelihood by means of an MCMC algorithm that takes advantage of the exchange algorithm and the sampling technique of Sect. 3.1. This algorithm is almost as efficient as one assuming the normalisation constants are readily available.

3.1 Rejection sampling from the COM-Poisson distribution

This section sets out a simple, yet efficient method for sampling from the COM-Poisson distribution without having to evaluate its normalisation constant. This method will be a key part of the exchange algorithm proposed in Sect. 3.4.

Suppose we want to generate a random variable Y from the COM-Poisson distribution with probability mass function $p(y|\varvec{\theta })=\frac{q_{\varvec{\theta }}(y)}{Z(\varvec{\theta })}$ where $\theta =(\mu ,\nu )$, $q_{\varvec{\theta }}(y)=\left( \frac{\mu ^{y}}{y!}\right) ^{\nu }$ and $Z(\varvec{\theta })=\sum _y q_{\varvec{\theta }}(y)$. Denote by m the mode of the COM-Poisson distribution, i.e., $m={\lfloor \mu \rfloor }$ and denote by $s=\lceil \sqrt{\mu }/\sqrt{\nu }\rceil$ its approximate standard deviation.

We construct an upper bound for the COM-Poisson distribution based on a piecewise geometric distribution. We start by defining three cut-off points, $m-s$, m, $m+s$. For the sake of simplicity, we assume that $m-s\ge 0$; otherwise, we can simply omit the part of the upper bound falling to the left of 0.

Now consider a distribution with p.m.f. proportional to

$$\begin{aligned} r_{\varvec{\theta }}(y)={\left\{ \begin{array}{ll} q_{\varvec{\theta }}(m-s)\cdot \left( \frac{m-s}{\mu }\right) ^{\nu \cdot (m-s-y)} &{} \text { for }y=0,\ldots ,m-s\\ q_{\varvec{\theta }}(m-1)\cdot \left( \frac{m-1}{\mu }\right) ^{\nu \cdot (m-1-y)} &{} \text { for }y=m-s+1,\ldots ,m-1\\ q_{\varvec{\theta }}(m)\cdot \left( \frac{\mu }{m+1}\right) ^{\nu \cdot (y-m)} &{} \text { for }y=m,\ldots ,m+s-1\\ q_{\varvec{\theta }}(m+s)\cdot \left( \frac{\mu }{m+s+1}\right) ^{\nu \cdot (y-m-s)} &{} \text { for }y=m+s,m+s+1, \ldots \end{array}\right. } \end{aligned}$$

(4)

By construction $r_{\varvec{\theta }}(y)\ge q_{\varvec{\theta }}(y)$.

For instance, if $y\in \{m+1,\ldots ,m+s-1\}$, then

$$\begin{aligned} q_{\varvec{\theta }}(y)^{1/\nu }= & {} \frac{\mu ^y}{y!}=\underbrace{\frac{\mu ^m}{m!}} _{=q_{\varvec{\theta }} (m)^{1/\nu }}\prod _{x=m+1}^y \underbrace{\frac{\mu }{x}}_{\le \frac{\mu }{m+1}} \nonumber \\\le & {} q_{\varvec{\theta }}(m)^{1/\nu } \left( \frac{\mu }{m+1}\right) ^{y-m} = r_{\varvec{\theta }}(y)^{1/\nu }. \end{aligned}$$

(5)

In contrast to the COM-Poisson distribution, the piecewise geometric distribution has a closed-form normalisation constant,

$$\begin{aligned} Z_g(\varvec{\theta })&=\sum _{y=0}^{\infty } r_{\varvec{\theta }}(y)=q_{\varvec{\theta }}(m-s)\frac{1- \left( \frac{m-s}{\mu }\right) ^{(m-s+1)\nu }}{1- \left( \frac{m-s}{\mu }\right) ^{\nu }}\nonumber \\&\quad +\,q_{\varvec{\theta }}(m-1)\frac{1-\left( \frac{m-1}{\mu }\right) ^{(s-1)\nu }}{1-\left( \frac{m-1}{\mu }\right) ^{\nu }}\nonumber \\&\quad +\,q_{\varvec{\theta }}(m)\frac{1-\left( \frac{\mu }{m+1}\right) ^{s\nu }}{1-\left( \frac{\mu }{m+1}\right) ^{\nu }}+q_{\varvec{\theta }}(m+s)\frac{1}{1- \left( \frac{\mu }{m+s+1}\right) ^{\nu }}.\nonumber \\ \end{aligned}$$

(6)

Clearly $Z(\varvec{\theta }) \le Z_g(\varvec{\theta })$. Then, letting $g_{\varvec{\theta }}(y) = P_{\varvec{\theta }}(Y=y) = \frac{r_{\varvec{\theta }}(y)}{Z_g(\varvec{\theta })}$ be the normalised p.m.f. corresponding to $r_{\varvec{\theta }}(y)$, one has that

$$\begin{aligned} p(y|\varvec{\theta }) = \frac{q_{\varvec{\theta }}(y)}{Z(\varvec{\theta })} \le \frac{r_{\varvec{\theta }}(y)}{Z(\varvec{\theta })} = \frac{Z_g(\varvec{\theta })}{Z(\varvec{\theta })} \frac{r_{\varvec{\theta }}(y)}{Z_g(\varvec{\theta })} = \frac{Z_g(\varvec{\theta })}{Z(\varvec{\theta })} g_{\varvec{\theta }}(y). \end{aligned}$$

This suggests sampling from $p(y|\varvec{\theta })$ using the rejection method, with $\frac{Z_g(\varvec{\theta })}{Z(\varvec{\theta })} g_{\varvec{\theta }}(y)$ as rejection envelope: a candidate y is drawn from $g_{\varvec{\theta }}(y)$ and accepted with probability

$$\begin{aligned} \frac{p(y|\varvec{\theta })}{\frac{Z_g(\varvec{\theta })}{Z(\varvec{\theta })} g_{\varvec{\theta }}(y)} = \frac{\frac{q_{\varvec{\theta }}(y)}{Z(\varvec{\theta })}}{\frac{Z_g(\varvec{\theta })}{Z(\varvec{\theta })} \frac{r_{\varvec{\theta }}(y)}{Z_g(\varvec{\theta })}} = \frac{q_{\varvec{\theta }}(y)}{r_{\varvec{\theta }}(y)}, \end{aligned}$$

which only involves unnormalised densities.

We can sample from $g_{\varvec{\theta }}(y)$ using a simple two-stage sampling procedure. First decide which part of the piecewise geometric distribution to sample from, according to probabilities proportional to the terms in (6). Then sample from the selected truncated geometric distribution using the inverse c.d.f. method, which is very efficient as the inverse c.d.f. is known in closed form.

The instrumental distribution in (4) is based on the same principle as the upper bounds used in the retrospective sampling algorithm proposed by Chanialidis et al. (2014). In contrast to the arbitrarily precise upper bound required for the retrospective algorithm, the bounds set out above are based on a trade-off between achieving a high acceptance rate while at the same time keeping the instrumental distribution simple so that sampling from it is computationally efficient. Figure 2 shows the rejection rate of the above sampling algorithm as a function of the two parameters $\mu$ and $\nu$. For most values of $\mu$ and $\nu$, the rejection rate is less than 30% and one can draw $10^6$ realisations from the COM-Poisson distribution in one second on a modern desktop computer (Intel Core i5).

Using a tighter rejection envelope (say by using more than four geometric pieces) yields a small reduction in the rejection rate, but overall the computational cost increases.

Finally, our proposed rejection algorithm in close in spirit to the basic adaptive rejection sampling technique (Gilks and Wild 1992) that constructs piecewise exponential proposal distributions which are adaptively refined using previously rejected samples.

Fig. 2

Rejection rate of the rejection sampler for the COM-Poisson distribution as a function of $\log (\mu )$ and $\log (\nu )$. The rejection rates were estimated based on samples of size $10^6$

3.2 Exchange algorithm

Møller et al. (2006) presented a Metropolis-Hastings algorithm for cases where the likelihood function involves an intractable normalisation constant that is a function of the parameters. The idea behind this algorithm is to enlarge the state of the Markov chain to include, beside the parameter $\varvec{\theta }$, an auxiliary variable $\varvec{y}^*$ defined on the same sample space as the data $\varvec{y} = (y_1, \ldots , y_n)$. Suitable choice of the proposal distribution ensures that the Metropolis-Hastings acceptance ratio is free of normalisation constants. Murray et al. (2006) proposed a modification, known as the exchange algorithm, which still generates at each step $\varvec{y}^*$, but only updates the parameter $\varvec{\theta }$ if the move is accepted. To describe this algorithm, let us suppose that the sampling model $p(y|\varvec{\theta })$ can be written as $p(y|\varvec{\theta }) = \frac{q_{\varvec{\theta }}(y)}{Z(\varvec{\theta })}$ where $q_{\varvec{\theta }}(y)$ is the unnormalised probability density and the normalisation constant $Z(\varvec{\theta }) = \sum _y q_{\varvec{\theta }}(y)$ or $Z(\varvec{\theta }) = \int q_{\varvec{\theta }}(y) \mathrm {d}y$ is unknown. This can easily be extended to the case where the $y_i$ are not i.i.d. (i.e., instead of $p(y|\varvec{\theta })$ and $q_{\varvec{\theta }}(y)$ we will have $p_i(y|\varvec{\theta })$ and $q_{i,\varvec{\theta }}(y)$ since the sampling model and its unnormalised probability density will be different for each observation).

For each MCMC update, first a candidate parameter $\varvec{\theta }^*$ is generated from the proposal distribution $h(\varvec{\theta }^*| \varvec{\theta })$; then auxiliary data $\varvec{y}^*$ are drawn from the sampling model $p(\varvec{y}^*|\varvec{\theta }^*)$, conditional on the candidate parameter value. The candidate $\varvec{\theta }^*$ is accepted with probability $\min \{1,a\}$. The computation of the acceptance ratio a is detailed below, where we contrast it with the acceptance ratio in a standard Metropolis-Hastings algorithm; in both we assume that the proposal density is symmetric in its two arguments, i.e., $h(\varvec{\theta }|\varvec{\theta }^*)=h(\varvec{\theta }^*|\varvec{\theta })$. In the exchange algorithm we have:

(7)

while in the Metropolis-Hastings algorithm:

$$\begin{aligned} a&=\frac{p(\varvec{y}|\varvec{\theta }^*)p (\varvec{\theta }^*) h(\varvec{\theta }|\varvec{\theta }^*)}{p(\varvec{y}|\varvec{\theta })p (\varvec{\theta }) h(\varvec{\theta }^*|\varvec{\theta })},\nonumber \\&=\frac{\left\{ \prod _{i}\frac{q_{\varvec{\theta ^*}}(y_i)}{Z(\varvec{\theta ^*})}\right\} p(\varvec{\theta }^*) h(\varvec{\theta }|\varvec{\theta }^*)}{ \left\{ \prod _{i}\frac{q_{\varvec{\theta }}(y_i)}{Z(\varvec{\theta })}\right\} p (\varvec{\theta }) h(\varvec{\theta }^*|\varvec{\theta })},\nonumber \\&=\frac{\left\{ \prod _{i}\frac{q_{\varvec{\theta ^*}}(y_i)}{Z(\varvec{\theta ^*})}\right\} p(\varvec{\theta }^*) }{\left\{ \prod _{i}\frac{q_{\varvec{\theta }}(y_i)}{Z(\varvec{\theta })}\right\} p (\varvec{\theta }) }. \end{aligned}$$

(8)

Notice how the acceptance ratio a for the standard Metropolis-Hastings algorithm involves the ratio of normalisation constants $\frac{Z(\varvec{\theta })}{Z(\varvec{\theta }^*)}$, which makes its computation hard. In the expression for the exchange algorithm, the ratio $\frac{Z(\varvec{\theta })}{Z(\varvec{\theta }^*)}$ cancels out and it is replaced by $\frac{q_{\varvec{\theta }}(y_i^*)}{q_{\varvec{\theta }^*}(y_i^*)}$, suggesting that the latter can be thought of as an importance sampling estimate for the former. We refer to Murray et al. (2006) for further discussion of the exchange algorithm.

Recently, Lyne et al. (2015) provided the first practical and asymptotically correct MCMC method for doubly intractable distributions that does not require exact sampling. This was done by constructing unbiased estimates of the reciprocal normalisation constant $1/Z(\theta )$ using unbiased estimates of $Z(\theta )$ obtained by importance sampling. The pseudo-marginal approach by Andrieu and Roberts (2009) is then adapted to use these estimates to form an MCMC algorithm. Finally, Wei and Murray (2016) construct unbiased estimates of reciprocal normalisation constants by applying Russian roulette truncations to a Markov chain rather than an importance sampler. However, given that we can draw exact samples from the COM-Poisson distribution at very little computational cost there is no need to resort to these methods.

We discuss next the prior distributions for the regression coefficients $\varvec{\beta }$ and $\varvec{\delta }$ in the COM-Poisson regression model in (3).

3.3 Choice of prior for the regression coefficients

For the priors of the regression coefficients, one can choose between a plethora of distributions. For the rest of the paper we will focus on three Bayesian COM-Poisson regression models; each one with a vague multivariate normal prior on $\varvec{\beta }$ and a different prior for $\varvec{\delta }$. The first model uses vague multivariate normal priors for both the regression coefficients $\varvec{\beta }$ and $\varvec{\delta }$ with mean zero and a variance of $10^6$, while the other two models use a shrinkage prior (lasso or spike and slab) for $\varvec{\delta }$. The motivation behind using a penalty for large values of the regression coefficients of the variance is not just variable selection. Putting a penalty on the coefficients is a way of having the Poisson regression model as the “baseline” model. The aforementioned models can be specified as:

where the first column represents a model with a lasso prior, while the second column represents a model with a spike and slab prior. The first model uses a conditional (on the variance) Laplace prior for the regression coefficients $\varvec{\delta }$ and takes advantage of the representation of the Laplace as a scale mixture of normals with an exponential mixing density (Park and Casella 2008). The maximum a posteriori (MAP) solution, under the aforementioned Laplace prior, is identical to the estimate for the standard (non-Bayesian) lasso procedure. The idea behind the second model is that the prior of every regression coefficient is a mixture of a point mass at zero and a diffuse uniform distribution elsewhere. This form of prior is known as a spike and slab prior (Mitchell and Beauchamp 1988). The parameter $\omega$ controls how likely each of the binary variables ${\phi }_j$ is to equal 1. Since it controls the size of the models, it can be seen as a complexity parameter.

3.4 MCMC sampling

For the COM-Poisson regression model, the acceptance ratio in (7) for the exchange algorithm becomes

$$\begin{aligned} a=\frac{\left\{ \prod _{i} q_{\varvec{\theta ^*}}(y_i)\right\} p(\varvec{\beta }^*)p (\varvec{\delta }^*) \left\{ \prod _{i} q_{\varvec{\theta }}(y_i^*)\right\} }{\left\{ \prod _{i} q_{\varvec{\theta }}(y_i)\right\} p(\varvec{\beta })p(\varvec{\delta }) \left\{ \prod _{i} q_{\varvec{\theta ^*}}(y_i^*)\right\} }, \end{aligned}$$

(9)

where $\varvec{\theta }=(\varvec{\beta }, \varvec{\delta })$. In the sampler, we make use of two different kinds of moves, in order to reduce the correlation between successive samples of the regression coefficients $\varvec{\beta }$ and $\varvec{\delta }$. Each sweep of the MCMC sampler performs these two moves in a sequence. The first proposes a move from $\varvec{\beta }$ to $\varvec{\beta }^*$ and afterwards from $\varvec{\delta }$ to $\varvec{\delta }^*$. The second proposes a move from ($\beta _i,\delta _i$) to ($\beta _i^*,\delta _i^*$) for $i=1,2, \ldots , p$, where p is the number of variables. The first move is meant to address posterior correlation between coefficients of different covariates. The second move is meant to address posterior correlation between coefficients for the mean and coefficients for the dispersion.

The two kinds of moves of the MCMC algorithm can be specified as

• A. First kind:

  • 1. We draw $\varvec{\beta }^*\sim h(\cdot |\varvec{\beta })$ where the proposal h() is a multivariate Gaussian centred at $\varvec{\beta }$. Specifically,

    

    where for the unnormalised COM-Poisson densities in (9) we have,

    $$\begin{aligned} q_{\varvec{\theta _i}}(y_i)&=\left( \frac{\mu _i^{y_i}}{y_i!}\right) ^{\nu _i},&q_{\varvec{\theta _i^*}}(y_i)&=\left( \frac{(\mu _i^*)^{y_i}}{y_i!}\right) ^{\nu _i^*},\nonumber \\ q_{\varvec{\theta _i}}(y_i^*)&=\left( \frac{\mu _i^{y_i^*}}{y_i^*!}\right) ^{\nu _i},&q_{\varvec{\theta _i^*}}(y_i^*)&=\left( \frac{(\mu _i^*)^{y_i^*}}{y_i^*!}\right) ^{\nu _i^*}. \end{aligned}$$

    (11)

  • 2. We now draw $\varvec{\delta }^*\sim h(\cdot |\varvec{\delta })$ where the proposal h() is a multivariate Gaussian centred at $\varvec{\delta }$. Specifically,

    

    where the unnormalised COM-Poisson densities can be evaluated as in (11).

• B. Second kind: For $j=1, \ldots , p$:

  • We draw $\beta _j^*\sim h(\cdot |\beta _j)$ and $\delta _j^*\sim h(\cdot |\delta _j)$ where the proposal distribution h() is a univariate Gaussian centred at $\beta _j, \delta _j$ respectively and for $l\ne j$ copy $\beta ^*_{l}=\beta _{l}$ and $\delta ^*_{l}=\delta _{l}$. Specifically,

    

    where the unnormalised COM-Poisson densities can be evaluated as in (11).

Each sweep of the MCMC algorithm performs both aforementioned moves i.e., we first update $(\beta _i, \delta _i)$ for $i=1, \ldots , p$ and then update $\varvec{\beta }$ and $\varvec{\delta }$ separately; there are $p+2$ accept/reject decisions within each iteration of the MCMC algorithm.

In order to assess the computational efficiency of the proposed MCMC sampler, we have compared the effective sample size (ESS) per second of the proposed method to the one of a vanilla MCMC sampler for Poisson regression. We have simulated Poisson-distributed data (i.e., $\nu =1$), for which the latter sampler has used the closed-form expression of the normalisation constant. The ESS per second in the latter case is only 10 times higher than the one for our proposed MCMC sampler, i.e., in order to get the same effective sample size the proposed method takes about 10 times as long. This factor of about 10 can be broken down into a factor of about 2 caused by the slower mixing of the exchange algorithm and a factor of about 5 caused by the higher computational cost of evaluating the acceptance ratio.

4 Simulation and case studies

4.1 Simulation

As already mentioned, the COM-Poisson regression model is a flexible alternative to count data models typically used in the literature, such as Poisson or negative binomial regression. The key strength of the COM-Poisson regression model is its ability to differentiate between a covariate’s effect on the mean of the response variable and its effect on the (excess) variance. This can be seen if we simulate from the overdispersed Poisson regression model (3), with

$$\begin{aligned} \varvec{x}_i&=(1,x_{i1},x_{i2},x_{i3},x_{i4})^\intercal ,\;&\varvec{\beta }&=(0,0,0,0.3,2)^\intercal ,\nonumber \\ \eta _i&= \varvec{x}_i^\intercal \varvec{\beta },\;&Y_i&\sim \text {Poi}(\exp (\eta _i)), \end{aligned}$$

(14)

where $x_{ij} \mathop {\sim }\limits ^{iid} \text {U}(-1,1)$, $j=1, 2, 3$ and $x_{i4}|x_{i3}\sim \text {U}(-a_i,a_i)$ with $a_i=\sqrt{\frac{1-x_{i3}}{2}}$ (for $i=1, 2, \ldots , n$, where n is the number of observations). In this setup the range, and thus the dispersion, of $x_{i4}$ depends on $x_{i3}$. The larger $x_{i3}$, the smaller the dispersion of $x_{i4}$. However, $x_{i3}$ and $x_{i4}$ are uncorrelated.

An overdispersed regression model is then obtained by omitting $x_{i4}$ from the model specification, which corresponds to $x_{i4}$ not being directly observable. Because $x_{i3}$ is related to the dispersion of $x_{i4}$, the degree of overdispersion of $Y_i$ depends on $x_{i3}$ as well. In this case, the third covariate has a positive effect on the mean of the response variable (i.e., the value of the regression coefficient is positive) and a negative effect on its variance since higher values of $x_{i3}$ will result in smaller dispersion for the covariate $x_{i4}$. Thus, the dispersion of the response variable will also be smaller. Figure 3 shows the relationship between the response variables and the two covariates $x_{i3}$ and $x_{i4}$.

Our intention behind this simulation is not model selection; our aim is to show that the parameter estimates from both the Poisson and negative binomial models may be distorted due to the effects of some covariates on the variance of the response variable.

Fig. 3

Scatterplot matrix which focuses on the relationship between the response variables and the covariates $x_{i3}$ and $x_{i4}$

Fig. 4

Simulation: 95 and 68% credible intervals for the regression coefficients of $\mu$. The latter are plotted with a shorter and thicker line

Fig. 5

Simulation: 95 and 68% credible intervals for the regression coefficients of $\nu$. The latter are plotted with a shorter and thicker line

We simulate $n=1000$ observations, which have empirical mean and variance of 1.36 and 2.37, respectively. The 95 and 68% credible intervals for the coefficients for the Poisson, negative binomial, and COM-Poisson regression model can be seen in Figs. 4 and 5. Figure 4 shows the credible intervals for the regression coefficients of $\mu$ for all the models.

The results for the Poisson and negative binomial models both lead to the conclusion that the third covariate has a negative effect on the mean of the response variable. This happens due to the covariate having a negative effect on the variance of the response variable. On the other hand, the COM-Poisson regression model correctly identifies all regression coefficients for the mean of the response variable. The credible intervals for the regression coefficients of $\nu$ for the COM-Poisson model can be seen in Fig. 5. The only posterior credible interval that does not include zero is the one for the third covariate (the one for the intercept is also wholly positive, although the lower end is very close to 0).

In order to generalise the results of the previous simulation, we have simulated 100 different samples from the model in (14) each one comprised of $n=1000$ observations. The results can be seen in Table 1. The Poisson and negative binomial models conclude that there is a positive effect of the third covariate on the response variable, in only 6 and 5 samples respectively. The COM-Poisson, on the other hand, infers a positive effect of the third covariate in 80 samples.

Table 1 Number of times, out of 100 different replications of the model in (14), that the 95% credible interval for the coefficient of the third covariate is wholly negative, includes 0, or is wholly positive

4.2 Publications by Ph.D. students

Long (1990) examined the effect of education, marriage, family, and the mentor on gender differences in the number of published papers during the Ph.D. studies of 915 individuals. The population was defined as all male biochemists who received their Ph.D.’s during the periods 1956–1958 and 1961–1963 and all female biochemists who obtained their Ph.D.’s during the period 1950–1967. Some of the variables that were used in the paper are shown in Table 2. For ease of interpretation, we standardise all non-binary covariates by subtracting their mean and dividing by their standard deviation.

Table 2 Description of variables

The study found, amongst other things, that females and Ph.D. students having children publish fewer (on average) papers during their Ph.D. studies. In addition, having a mentor with a large number of publications in the last three years has a positive effect on the number of publications of the Ph.D. student. We will focus on the students with at least one publication (640 individuals) with empirical mean and variance of 1.42 and 3.54, respectively, a sign of overdispersion. Note that after focusing on the students with at least one publication, we subtract 1 from each student’s number of publications (e.g. the 246 students that had 1 publication in the original dataset are represented with a 0 in the final dataset). Removing the students with no publications (275 students out of the 915 students in the original dataset) allows us to fit a simple parametric model on the subset instead of a more complex alternative on the original dataset (e.g. zero-inflated model, hurdle model, non-parametric model). Thus, we only compare the Poisson, negative binomial, and the COM-Poisson regression models.

Figure 6 shows the 95 and 68% credible intervals for the regression coefficients of $\mu$ for all the regression models. The Poisson and negative binomial models have similar results. The only difference between them is that for the latter model the 95% posterior interval on the effect of having children includes zero. The gender of a Ph.D. student and the number of articles by the Ph.D. mentor are the only covariates that have credible intervals that do not include zero, for both the Poisson and negative binomial models.

Fig. 6

Publication data: 95 and 68% credible intervals for the regression coefficients of $\mu$. The latter are plotted with a shorter and thicker line

Fig. 7

Publication data: 95 and 68% credible intervals for the regression coefficients of $\nu$. The latter are plotted with a shorter and thicker line

Specifically, these models conclude that female Ph.D. students publish less on average than male Ph.D. students and that a mentor who has published a lot of articles has a positive effect on the number of articles of the Ph.D. student. On the other hand for the COM-Poisson models, the previous two covariates seem to not have an effect on the mean of the number of articles published by a Ph.D. student. It must be noted that there are four male Ph.D. students with a large number of articles published (11, 11, 15, 18) that could be considered as outliers. If these four students are taken out of the data set, the gender covariate does not have a significant effect for the Poisson and negative binomial models. In addition, the empirical means of the male and female Ph.D. students are 1.5 and 1.2, respectively, while the empirical median is 1 for both genders. Thus the COM-Poisson regression model seems to be doing a better job at not concluding that there is an effect of the gender covariate.

Figure 7 shows the 95 and 68% credible intervals for the regression coefficients of $\nu$ for the COM-Poisson regression models. This figure shows that there seems to be a positive effect of the “mentor” covariate on the variance of the articles of the Ph.D. student. The more articles a mentor publishes (during the last 3 years) the larger the variance for the number of articles published by a Ph.D. student. This seems to be reinforced further when we look at the empirical variance of students having mentors with an above average number of articles published versus students having mentors with less than average number of articles published. The empirical variance for the former group is 5.8, with the latter group having a variance of 2.1, respectively (ratio of around 2.8). The corresponding empirical means are 1.9 and 1.2 (ratio of around 1.6). In Poisson-distributed data, one would expect the ratios to be roughly equal.

4.3 Fertility data

This section uses data from Winkelmann (1995) on the number of births given by a cohort of women in Germany. The data consist of 1243 women over 44 in 1985. The explanatory variables that were used can be seen in Table 3.

Table 3 Description of variables

The empirical mean and variance of the response are 2.39 and 2.33, respectively. The unconditional variance is already slightly smaller than the unconditional mean. Including covariates the conditional variance will reduce further, thus suggesting that the data show underdispersion. For this reason, the negative binomial model was not used in this context. The results can be seen in Figs. 8 and 9. The credible intervals for the coefficients of $\mu$ are similar across all the models. Looking at Fig. 9 we can see the credible intervals for the coefficients of $\nu$. The posterior intervals that do not include zero refer to the vocational education, age, and age at marriage.

Fig. 8

Fertility data: 95 and 68% credible intervals for the regression coefficients of $\mu$. The latter are plotted with a shorter and thicker line

Fig. 9

Fertility data: 95 and 68% credible intervals for the regression coefficients of $\nu$. The latter are plotted with a shorter and thicker line

For model selection, we will use the deviance information criterion (DIC) by Spiegelhalter et al. (2002). This can be seen as a Bayesian alternative model selection tool to AIC and BIC. A smaller DIC indicates a better fit to the data set. The results for both data sets (published papers and fertility data) can be found in Table 4 and show that the COM-Poisson models outperform the Poisson and the negative binomial models in both examples.

Table 4 Deviance information criterion for all models and all data sets with the minimum DIC in bold

Fig. 10

Publication data: 95 and 68% credible intervals for the regression coefficients of $\mu$. The latter are plotted with a shorter and thicker line

5 Comparing MCMC algorithms for COM-Poisson regression models

Besides showing the flexibility the COM-Poisson distribution offers, the goal of this paper is to propose an MCMC algorithm for COM-Poisson regression models more efficient than the exact MCMC algorithm of Chanialidis et al. (2014). The main idea behind the algorithm given in Chanialidis et al. (2014) is to take advantage of a sequence of increasingly and arbitrarily precise lower and upper bounds on the likelihood, resulting in bounds on the target density and the acceptance probability of the Metropolis-Hastings algorithm. This sequence of arbitrarily precise bounds is created by increasing the number of terms that are computed exactly for the estimation of the normalisation constant and using piecewise geometric bounds for the remaining terms. Assuming that $\check{\pi }_n$ and $\hat{\pi }_n$ are the lower and upper bounds of the target density after n refinements, the proposed algorithm for deciding on the acceptance of $\theta ^*$ then proceeds as follows:

• 1. Draw $U \sim \text {Unif}(0,1)$ and set the number of refinements $n=0$.

• 2. Compute $\check{\pi }_n$ and $\hat{\pi }_n$ and compare them to U.

  • If $U\le \check{\pi }_n,$ accept the candidate value.

  • If $U>\hat{\pi }_n,$ reject the candidate value.

  • If $\check{\pi }_n< U < \hat{\pi }_n,$ refine the bounds, i.e increase n and return to step 2.

Fig. 11

Publication data: 95 and 68% credible intervals for the regression coefficients of $\nu$. The latter are plotted with a shorter and thicker line

Fig. 12

Publication data: Traceplots for the regression coefficients of $\mu$ for the exchange algorithm

Fig. 13

Publication data: Traceplots for the regression coefficients of $\mu$ for the bounds algorithm

Fig. 14

Publication data: Traceplots for the regression coefficients of $\nu$ for the exchange algorithm

Fig. 15

Publication data: Traceplots for the regression coefficients of $\nu$ for the bounds algorithm

Table 5 Effective sample size per minute for the regression coefficients of $\mu$

Table 6 Effective sample size per minute for the regression coefficients of $\nu$

We will now compare the algorithm presented in Chanialidis et al. (2014) with the MCMC algorithm presented in this paper, using the publications data discussed in Sect. 4.2. Both MCMC algorithms include the two kinds of moves presented in Sect. 3.4, have a burn-in period of 20,000 iterations and a posterior sample size of 60,000.

Figures 10 and 11 show the 95 and 68% credible intervals for the regression coefficients of $\mu$ and $\nu$ for both MCMC algorithms. It can be seen that the “exchange” MCMC gives similar results as the “bounds” MCMC.

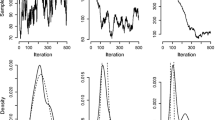
Traceplots for the regression coefficients of $\mu$ can be seen in Figs. 12, 13, while the traceplots for the regression coefficients of $\nu$ can be seen in Figs. 14, 15. Both MCMC algorithms seem to mix well.

The main difference between the two algorithms is the computation time. For the “exchange” MCMC algorithm the computation time was 14 min, while the “bounds” MCMC algorithm needed 238 min for the same number of iterations, seventeen times longer. A similar difference on the computation time is seen on the fertility data set.

Tables 5 and 6 show the effective sample sizes (ESS) per minute for the regression coefficients of $\mu$ and $\nu$ respectively. In both tables and across all the regression coefficients, the “exchange” MCMC outperforms the “bounds” MCMC algorithm. The average ESS per minute for the “exchange” MCMC is 123.01 while for the “bounds” MCMC is 11.94.

Fig. 16

Publication data: Scatterplot of the parameters $\mu$ and $\nu$

Figure 16 shows the scatterplot of the parameters $\mu _i$, $\nu _i$ for $i=1, \ldots , 640$. The parameters $\mu _i$, $\nu _i$ were obtained using the posterior sample of the “exchange” algorithm and substituting the posterior mean of each regression coefficient $\beta _j, \delta _j$ for $j=1, \ldots , 6$ in Eq. (3).

Figure 17 shows the conditional mean and variance approximations (on the log scale) seen at the start of Sect. 2. The x-axes refer to the right-hand side of the Eq. (2), while the y-axes refer to the mean and variance of a COM-Poisson distribution with parameters $\mu _i$, $\nu _i$. In order to compute the mean and variance, we first estimated the probability mass function of the COM-Poisson distribution evaluation the normalisation constant $Z(\mu _i,\nu _i)$ and then used the definitions of the mean and variance of a distribution. Figure 18 shows a scatterplot of the conditional mean versus the conditional variance. The dotted line refers to the case where the conditional mean is equal to the conditional variance. In this case all the points are above the line, a sign of overdispersion.

Fig. 17

Publication data: Mean and variance approximations

Finally, we have used both MCMC algorithms on the publications and fertility data sets, with 5 different starting values and the “exchange” MCMC algorithm consistently outperforms the “bounds” MCMC. Due to constraints of space, we have only shown the results for one of those seeds on the smaller data set (i.e., publications data set).

Fig. 18

Publication data: conditional mean versus conditional variance

R (R Core Team 2015) was used for all the computations in this paper. Traceplots, density plots, autocorrelation plots (for every regression coefficient) and results for the Gelman and Rubin diagnostic, Gelman and Rubin (1992), were employed to assess convergence of the MCMC samplers to the posterior distribution, using the coda package (Plummer et al. 2006). The plots for the credible intervals and the traceplots of the regression coefficients were made using the mcmcplots package (Curtis 2015).

The code for both MCMC algorithms (“exchange” and “bounds”) is now available on Github.¹

6 Conclusions

In this paper, we presented a computationally more efficient MCMC algorithm for COM-Poisson regression compared to the alternative in Chanialidis et al. (2014). We showed how rejection sampling, combined with the exchange algorithm, can be used to overcome the problem of an intractable likelihood in the COM-Poisson distribution. Finally, this allowed us to use a Bayesian COM-Poisson regression model and show its benefits, compared to the most common regression models for count data, through a simulation and two real-world data sets.