Abstract
We introduce a new class of data-fitting energies that couple image segmentation with image restoration. These functionals model the image intensity using the statistical framework of generalized linear models. By duality, we establish an information-theoretic interpretation using Bregman divergences. We demonstrate how this formulation couples in a principled way image restoration tasks such as denoising, deblurring (deconvolution), and inpainting with segmentation. We present an alternating minimization algorithm to solve the resulting composite photometric/geometric inverse problem. We use Fisher scoring to solve the photometric problem and to provide asymptotic uncertainty estimates. We derive the shape gradient of our data-fitting energy and investigate convex relaxation for the geometric problem. We introduce a new alternating split-Bregman strategy to solve the resulting convex problem and present experiments and comparisons on both synthetic and real-world images.
Similar content being viewed by others
1 Introduction
1.1 Image-Processing Tasks as Inverse Problems
Image-processing tasks are commonly formulated as inverse problems aiming at reconstructing targeted features from a set of observed images (Bertero and Boccacci 1998; Aubert and Kornprobst 2006; Chan and Shen 2005; Vogel 2002; Hansen et al. 2006, and references therein). The objectives differ according to the nature of the features of interest. On the one hand, image restoration is a low-level vision task aiming at reconstructing photometric properties degraded by the imaging process (Chan and Shen 2005). For example, image denoising aims at filtering the stochastic fluctuations intrinsic to the imaging process (Bovik 2005); image deblurring consists in removing imaging imperfections due to limitations of the optics (optical blur), motion (motion blur), or medium-induced distortions; image interpolation (e.g., inpainting, zooming, super-resolution) aims at reconstructing image parts that are unresolved, missing, or deteriorated. On the other hand, image segmentation bridges low- and high-level tasks and is the first step to image analysis. It aims at partitioning an image into “meaningful” regions defined by priors about the properties of a region. Regions are frequently defined through their intensity, color, texture, or motion (Chan and Shen 2005; Cremers et al. 2007; Brox et al. 2010).
Inverse problems in image processing are often ill-posed or ill-conditioned (Bertero et al. 1988). One principled way of regularizing them is to use a Bayesian formulation (Geman and Geman 1984; Mumford 1994; Zhu and Yuille 1996; Kersten et al. 2004; Cremers et al. 2007). In this framework, the image-processing task is formalized by the posterior probability of the data. This has a clear modeling advantage, because the posterior probability splits into two terms: the image likelihood (or the probability of observing the image data knowing the features) and the prior probability of the features before having observed the image. The image likelihood (data-fitting term) quantifies the consistency between the observed image and a subset of candidate features. It is usually easier to model than the posterior probability, because it can often be derived from a generative model (forward model) of the image-formation process. The prior encodes expected properties of the solution of the inverse problem. It acts as a regularizer by constraining the set of admissible solutions, hence helping cope with missing or low-quality data. This is the property of Bayesian formulations that allows them to transform an initially ill-posed problem into a well-posed one.
1.2 Data-Fitting Energies
The anti-logarithm of the posterior probability links the Bayesian inverse problem to energy minimization (Geiger and Yuille 1991; Mumford 1994; Zhu and Yuille 1996). The objective functional is expressed as a linear combination of a data-fitting energy and a prior energy, weighted by a regularization parameter tuning the trade-off between fidelity and robustness of the reconstruction. For a given image-processing task, one needs to design a “suitable” energy functional. Over the past years, a wealth of energy functionals have been proposed for different situations, and insights have been gained into their rationales and implications. Nevertheless, the link between a given data-fitting energy and the likelihood function of the underlying statistical model may remain unclear, as energy functionals are often designed without basing them on a specific statistical model.
When a forward model for the image-formation process is available, a data-fitting energy is straightforwardly designed by introducing the anti-log-likelihood function of the underlying statistical model. For example, many detectors operate in a regime where a Poisson noise model applies (Bovik 2005), such as in confocal microscopy (Dey et al. 2004; Art 2006), emission tomography (Shepp and Vardi 1982), or single-photon emission computed tomography (Hebert and Leahy 1989). This results then in a Poisson anti-log-likelihood functional. Similarly, Gamma distributions can be used to model multiplicative noise, such as speckles (Aubert and Aujol 2008). More generally, data-fitting energies can be chosen from a large family of statistical models, such as the exponential family (EF), introduced to the image-processing community by Chesnaud et al. (1999).
Yet, data-fitting energies can also be devised without any explicit link to a statistical model. One common choice is to use a metric induced by a norm pertaining to a vector space. The choice of data-fitting energy then relies on the fine structure of the underlying function space (see Aujol et al. 2006, and references therein). However, in some instances a link to an underlying statistical model can be established. For example, the squared \(L^2\) norm is often used as a data-fitting energy and corresponds to the classical least-squares criterion. The statistical rationale is that this data-fitting energy is (up to additive constants) the anti-log-likelihood of a linear forward model with additive Gaussian noise. More recently, it has been suggested to replace the \(L^2\) data-fitting term by an \(L^1\) term in order to cope with outliers, such as in salt-and-pepper denoising (Alliney 1997; Nikolova 2004). Statistically, using an \(L^1\) norm can be motivated by modeling the noise with a Laplace distribution where the probability of large deviations from the mean is not negligible compared to a Gaussian model. Denoising using a \(L^1\) data-fidelity term is robust against outliers, as the best estimate of the parameter in this case amounts to a median filter known to remove impulse noise (Bovik 2005).
To the best of our knowledge, a systematic study of the link between the functional form of data-fitting energies and the underlying statistical forward model is missing in the literature. We can expect that being a metric is a requirement too stringent to qualify a functional as a valid data-fitting energy. For example, the Poisson anti-log-likelihood can be identified with the Kullback-Leibler divergence, which is not a metric (neither symmetry nor the triangle inequality are satisfied).
1.3 Coupling Image Restoration and Segmentation
The difference between image restoration and segmentation is that in the former the objects composing the scene are implicitly assumed through their effect on the features of the image (such as edges and object boundaries), whereas in the latter objects are explicitly represented and the set of object boundaries is an explicit argument of the inverse problem. In image restoration, the effects of objects are modeled in the hypothesis one makes about the underlying mathematical structures involved in the formulation of the image model (Chan and Shen 2005). Since the work of Rudin et al. (1992), the space of functions of bounded variation has been known as a good model for images, since it implies a balance between penalizing irregularities, often due to noise, and respecting intrinsic image features like edges. In image segmentation, the primary goal is to estimate the number, positions, and boundaries of objects present in the imaged scene.
Edge-based (Kass et al. 1988; Caselles et al. 1997) algorithms achieve image segmentation working with edge cues only, and segmentation amounts to estimating the positions of edges. These models only use local information and are therefore sensitive to noise. Region-based approaches (Chan and Vese 2001; Paragios and Deriche 2002) are based on the observation that specifying an edge set is equivalent to specifying a partition of the image domain into regions. Apart from their increased robustness to noise, region-based models have the advantage of explicitly modeling the photometric properties of the regions, and the forward problem is therefore more flexible than in a purely edge-based approach.
However, the two approaches are not exclusive, and edge information can also be integrated into region-based models (Zhu and Yuille 1996; Paragios and Deriche 2002; Bresson et al. 2007). The Mumford-Shah model (Mumford and Shah 1989) is an example of a minimal model including both region and edge information. Different other models can be recovered by specializing it (Chan and Shen 2005). Therefore, an image restoration task can potentially be turned into a segmentation problem by explicitly representing the edge set to be estimated. The resulting inverse problem is then composite with two unknowns: the edge set of the region boundaries and the photometric properties within each region. See Helmuth and Sbalzarini (2009); Helmuth et al. (2009), and Jung et al. (2009) for instances of an image segmentation/deblurring coupling, and Leung and Osher (2005) for an instance of an image inpainting/segmentation coupling.
1.4 Image Segmentation Algorithms
Once a well-posed formulation is found, its numerical solution by an efficient algorithm is crucial for practical usability. These two aspects—the mathematical model and its algorithmic implementation—are to be considered concomitantly in order to match the level of detail in the mathematical description with the algorithmic efficiency required by the application.
Bayesian image models can be formulated either discretely or continuously. The formulation then directly defines the class of algorithms that can be used to minimize the associated energy. Different formulations can therefore lead to optimization problems with qualitatively different properties. The ability of a given algorithm to find global or local minima in reasonable time and with theoretical guarantees is crucial for practical applications. In a discrete setting, such as in Markov random fields, Geman and Geman (1984) introduced Gibbs sampling and used an annealing strategy to minimize discrete energies from a Bayesian formulation of image restoration. Greig et al. (1989) were the first to propose the use of graph cuts to minimize exactly a two-label image model. This was later extended to efficiently finding the exact minimum of approximate energy functionals (Boykov et al. 2001). More recently, Cardinale et al. (2012) introduced an efficient particle-based algorithm to compute local minimizers of complex discrete energies under topology constraints.
In continuous formulations, variational calculus can be used to derive gradients or higher-order quantities necessary for iterative minimization schemes such as gradient descent or Newton’s method (see e.g., Hansen et al. 2006; Vogel 2002; Aubert and Kornprobst 2006; Chan and Shen 2005). Active contours (Kass et al. 1988) and their level-set implementation (Caselles et al. 1993; Malladi et al. 1995; Osher and Fedkiw 2003; Osher and Paragios 2003; Sethian 1999) are popular algorithms to solve the resulting segmentation problem. A continuous formulation allows accurately representing object boundaries (i.e., to sub-pixel resolution), but suffers from the fact that the energy of the associated free-surface problem is non-convex. Therefore, any local minimizer, such as gradient descent, will converge to a local minimum, hence requiring careful initialization. Chan et al. (2006) and Bresson et al. (2007) introduced an exact convex relaxation of an extended version of the two-region piecewise-constant Mumford-Shah model, also known as the Chan-Vese model (Chan and Vese 2001), and for the two-region piecewise-smooth Mumford-Shah model. This new formulation enables using efficient convex optimization algorithms, such as split-Bregman techniques (Goldstein and Osher 2009; Goldstein et al. 2010; Paul et al. 2011), to solve the segmentation problem in a fast and accurate way.
1.5 Scope and Contributions of the Present Work
Here we introduce a new class of data-fitting energy functionals for two-region segmentation of scalar-valued images. These energies are derived from a generalized linear model (GLM) formulation of the photometric properties of the image, extending energy functionals based on the exponential family (EF) as proposed by Lecellier et al. (2006, 2010). We extend the EF image model by introducing (i) a linear predictor accounting for transformations during the imaging process and (ii) a possibly non-linear relationship between the observed data and the linear predictor through a link function. We show that many known statistical models are special cases of our energy functional, and we also demonstrate how our formulation succeeds in coupling segmentation in a principled way with image restoration tasks, such as denoising, deconvolution, and TV-inpainting. We use the duality between the regular exponential family (REF) of distributions and regular Bregman divergences in order to reformulate our model in an information-theoretic framework, where the data-fitting energy is written as the integral over the image domain of a Bregman divergence. This clarifies the link between an entire class of statistical forward models (GLMs) and an information-theoretic criterion (Bregman divergences). As a prior, we use the classical total variation (TV) regularizer. Therefore, we call our new image model GLM/Bregman-TV.
A second aspect of this work is the design of algorithms for solving the composite photometric/geometric optimization problem resulting from the present class of energies. We propose a simple alternating minimization (AM) scheme, solving sequentially the photometric and the geometric inverse problems. This allows us to separately treat inverse subproblems that could be reused also in other solvers. Adapting results from the GLM literature, we show that a variant of Newton’s method, the Fisher scoring algorithm, can be used to solve the photometric estimation problem and obtain information about the asymptotic estimation uncertainty. For the geometric estimation, we derive the shape gradient of our data-fitting energy, which can be used in any level-set algorithm. Extending previous results (Chan et al. 2006; Bresson et al. 2007), we further show that if the image-formation transformation is the identity one can obtain an exact convex relaxation by thresholding of the solution of the resulting optimization problem, whereas in the general case this is not possible. For the general case, however, we provide an upper bound on the energy difference between the solution of the relaxed convex problem and the global solution of the original non-convex problem. The relaxed problem is solved using a novel formulation of the alternating split-Bregman (ASB) algorithm (Goldstein et al. 2010) with a splitting strategy inspired by Setzer et al. (2010). We assess the performance and quality of our approach on both synthetic and real-world examples and compare it with existing state-of-the-art methods.
2 The GLM/Bregman-TV model
We extend the EF noise model introduced to image segmentation by Chesnaud et al. (1999); Martin et al. (2004), and Lecellier et al. (2010) by integrating image-restoration tasks, such as TV-inpainting and deconvolution. We first present the GLM formulation and show its flexibility in coupling image segmentation and restoration. Then, we provide an information-theoretic interpretation of our new class of energies.
2.1 Generalized Linear Models (GLM)
Nelder and Wedderburn (1972) introduced GLMs as a flexible extension of linear regression that allows for different stochastic data-generation processes and for a potentially non-linear relationship between the explanatory variables of the linear model and the response variable.
A GLM is composed of three components: a random component, a systematic component (linear predictor), and a parametric link function. The random component specifies the probability density function (p.d.f.) \(p\) of the response variable \(u_0({{\varvec{x}}})\) (in our case the intensity at pixel \({{\varvec{x}}}\)) as a member of the EF. The corresponding log-likelihood is:
where \(a(\cdot ),\,b(\cdot )\), and \(c(\cdot )\) are known functions, \(\phi \) is a known scalar called the scale parameter (or dispersion), and \(\theta \) is called the natural parameter (McCullagh and Nelder 1989). For an introduction to the EF in image segmentation, we refer to the works of Goudail et al. (2003), Martin et al. (2004), and Lecellier et al. (2010). The function \(a\) is a positive function called the dispersion function. It is directly related to the variance of the p.d.f. (see Eq. 3). The function \(b/a\) is the so-called cumulant generating function or log-partition function of the p.d.f. Here we assume that the natural parameter space \(\varTheta = \left\{ \theta : b(\theta ) < \infty \right\} \) is open, which entails that we consider only regular exponential families (REF) of distributions.Footnote 1 The function \(\exp (c)\) is called the reference measure and is independent of the parameters. It therefore plays no role in the estimation, as \(\phi \) is assumed known.
Lecellier et al. (2010) state results about the EF and derive the corresponding data-fitting energies for region-based active contours. We refer to their paper for theoretical results in this context and for other noise models relevant to image processing with EF members that we do not show in this paper (cf. Table 1 in their article). The p.d.f. in Eq. (1) is a special case of the general treatment of the EF by Lecellier et al. (2010), in the sense that it is a one-parameter canonical EF with the identity function as its sufficient statistic (cf. Lecellier et al. (2010) for the definition of the sufficient statistics vector). The parametrization of the p.d.f. (1), however, is different from the one Lecellier et al. (2010) used, since it introduces the dispersion \(a\) for image-modeling purposes. The dispersion function \(a({{\varvec{x}}},\phi )\) is usually decomposed as \(a({{\varvec{x}}},\phi ) := \phi /w_d({{\varvec{x}}})\), where \(w_d\) represents known a priori weights of the data, and \(\phi \) is the scale parameter. When coupled with a regularization prior, the scale parameter can be absorbed into the regularization parameter. Therefore, we set \(\phi =1\) from now on without loss of generality.
In contrast to Lecellier et al. (2010), the natural parameter \(\theta \) is not of primary interest in a GLM. The objective rather is to model the mean of the p.d.f. generating the data. To this end, GLMs introduce two additional components: a linear predictor and a parametric link function. The linear predictor \(\eta \) models the systematic component as a linear function in \(\varvec{\beta }\) as \(\eta ({{\varvec{x}}},\varvec{\beta })\,{:=}\, \varvec{X}^{T}({{\varvec{x}}})\varvec{\beta }\). \(\varvec{X}\) is called the design matrix and \(\varvec{\beta }\) the vector parameter. The link function \(g\) is a known, smooth, monotonic mapping that models the potentially non-linear relationship between the mean \(\mu \) of the p.d.f. and the linear predictor as \(g(\mu ({{\varvec{x}}},\varvec{\beta })) = \eta ({{\varvec{x}}},\varvec{\beta })\).
Together, the link function \(g\) and the linear predictor \(\eta \) allow modeling the mean region intensity \(\mu \). In the next section and in Table 1, we provide examples of how to instantiate GLMs in order to systematically translate image-processing tasks into data-fitting energies. In general, the interpretation of the design matrix \(\varvec{X}\) and the vector parameter \(\varvec{\beta }\) depends on the link function (McCullagh and Nelder 1989). In image processing, however, it seems that the possible non-linearity of \(g\) has not yet been exploited,Footnote 2 and that \(g\) is implicitly assumed to be the identity. In this case, \(\varvec{\beta }\) models the mean image intensities.
We now list some properties of GLMs relevant for the results of this work. The mean \(\mu ({{\varvec{x}}},\varvec{\beta })\) and the variance \(\sigma ^2({{\varvec{x}}},\varvec{\beta })\) of the response variable \(u_0\) are related to \(a\) and \(b\) as:
where \(V(\cdot ) \,{:=}\, b^{\prime \prime }(\cdot )\) is the variance function (McCullagh and Nelder 1989). The last parametrization decomposes the different sources influencing the variance of the response variable: a data-dependent term with priorly known weights \(w_d({{\varvec{x}}})\), and a term depending on the model only via the mean \(\mu ({{\varvec{x}}},\varvec{\beta })\) through the variance function \(V\).
2.2 Whole-Image Anti-Log-Likelihood
Following Zhu and Yuille (1996), assuming the pixels within a region to be statistically independent, and taking the limit of a large number of pixels, we can define the whole-image data-fitting energy \(\mathcal{E }_\mathrm{d}^\mathrm{{GLM}}\) of \(u_0\) over the image domain \({\varOmega _I}\) as the integrated GLM anti-log-likelihood \(\ell (u_0~| {{\varvec{x}}}, \theta ) \,{:=}\, -\log p(u_0~| {{\varvec{x}}}, \theta )\):
The integral term involving \(c\) (cf. Eq. 1) plays no role in the estimation.
For the sake of simplicity, we consider a two-region piecewise-constant image model. The image domain is partitioned into a background region \(\varOmega _1\) and a foreground region \(\varOmega _2\). Each region is represented by a mask (indicator) function \(M_i({{\varvec{x}}}) \,{:=}\, \mathbf 1 _{\varOmega _i}({{\varvec{x}}})\) (\(i \in \left\{ 1,2\right\} \)) that is \(1\) if \({{\varvec{x}}}~\in \varOmega _i\) and \(0\) otherwise. The piecewise-constant model \(u\) can hence be algebraically represented as:
where \(\beta _1\) and \(\beta _2\) are the photometric constants of the background and the foreground, respectively.
We now show how the classical Chan-Vese model (Chan and Vese 2001) can be formulated as a GLM. This model expresses the data-fitting energy as the sum of a foreground and a background mean squared energy:
Due to the binary nature of the indicator functions, we can rewrite this energy as:
Introducing the design matrix \(\varvec{X}({{\varvec{x}}})= \varvec{M}({{\varvec{x}}})\), we recognize this energy as the anti-log-likelihood of a Gaussian with variance \(\sigma =1\) and mean \(\mu ({{\varvec{x}}},\varvec{\beta })~= \varvec{X}^{T}({{\varvec{x}}})\varvec{\beta }\). This statistical interpretation of the Chan-Vese energy is well known and it amounts to a GLM with \(\theta =\mu =\varvec{X}^{T}\varvec{\beta }\) (the link function \(g\) is the identity), \(b=1/2\mu , \,a=1\) (\(w_d(\cdot ) = 1\)), and \(c(u_0,1) = -1/2 u_0^2\). This model is known in statistics as a one-way ANOVAFootnote 3 (see, e.g., McCullagh and Nelder 1989), which models a set of observations (i.e., the pixel intensity values \(u_0\)) as a mixture of two subpopulations (i.e., foreground and background as indexed by \(\varvec{M}\)) characterized by their means (i.e., the mean intensity values \(\beta _1\) and \(\beta _2\)) observed after perturbation with additive and independent Gaussian noise of variance \(\sigma \).
Table 1 and Eq. (9) provide the necessary information to formulate also many other GLM energies. Segmentation is encoded in the piecewise-constant object model \(u({{\varvec{x}}},\varvec{\beta })\) (see Eq. 5 for \(N=2\) regions). Denoising is encoded in the choice of the REF member, defined either via Eq. (1) or via a Bregman divergence (9). As shown in Sect. 3, it is sufficient to specify the variance function \(V\) in order to identify a particular REF member when solving the inverse problem. Inpainting is encodedFootnote 4 by the prior weight \(w_d\). Deconvolution is encoded in the design matrix \(\varvec{X}\). Without deconvolution, \(\varvec{X}\) is identical to the matrix of masks \(\varvec{M}\), as in the Chan-Vese example above. With deconvolution, the point-spread function (PSF) \(\mathrm{K}\) enters the design matrixFootnote 5 as \(\varvec{X}({{\varvec{x}}})= \left( \mathrm{K}*\varvec{M}\right) ({{\varvec{x}}})\). Table 1 also shows how our new model allows systematically constructing new data-fitting energies. For example, coupling a \(N\)-region segmentation problem with deconvolution and inpainting (over \(\Omega ^\prime \)) results in the energy:
with \(w_d({{\varvec{x}}}) = \mathbf 1 _{{\varOmega _I}\setminus \varOmega ^\prime }({{\varvec{x}}})\) and \(\mu ({{\varvec{x}}},\varvec{\beta })~= (\mathrm{K}*\varvec{M})({{\varvec{x}}})^{T}\varvec{\beta }\).
2.3 Bregman Data-Fitting Energies
The p.d.f. in Eq. (1) is written in terms of the natural parameter \(\theta \) (“natural parametrization”), but the main intent of the GLM is to model the mean of the p.d.f. For the regular exponential family (REF), there is an alternative parametrization of the p.d.f. (1) that directly uses the mean \(\mu \) (“mean parametrization”). Barndorff-Nielsen (1978) pioneered the systematic study of this relationship. Following Banerjee et al. (2005), we investigate the duality between the natural and the mean parametrization using convex analysis in order to establish connections between the REF and Bregman divergences.
We recall the definition of the Bregman divergence \(\mathrm B _\psi (\cdot \!\parallel \! \cdot )\) associated with a continuously differentiableFootnote 6, real-valued, strictly convex function \(\psi :S \rightarrow \mathbb R \) defined on a closed, convex set \(S\). Then, for any pair of points \((p,q)\in S^2\),
This can be interpreted as the difference between the function \(\psi \) evaluated at \(p\) and its first-order Taylor approximation around \(q\), evaluated at \(p\).
In the following, we use the concept of a saturated model. In statistics, this is defined as a model having as many parameters as there are data points, using no regularization. In image processing, this would mean reconstructing one intensity value for each pixel. The saturated model hence reproduces the data and serves as a reference for any predictive model. The purpose of statistical modeling is to capture the essential features of the data in a reduced model (i.e., using only one intensity value per region) using prior knowledge (i.e., an appropriate regularizer), loosing as little fitting accuracy as possible. The saturated model has a higher likelihood than any alternative model. Minimizing the difference in anti-log-likelihood between the saturated model and the reduced model of interest thus amounts to achieving a tradeoff between a comprehensive model (i.e., foreground and background parameters) and a model best fitting the data (i.e., the saturated model).
We recall that the natural parameter \(\theta \) and the mean parameter \(\mu \) of the REF are in convex duality through \(b\) and its convex conjugate functionFootnote 7 \(b^\star (\mu )\). The following result states that the difference in log-likelihood between any REF model and the saturated model is given by a Bregman divergence.
Result 1
Consider a one-dimensional REF model with natural parameter \(\theta \) and mean parameter \(\mu \). Maximum likelihood estimators (MLE) under the saturated model are marked with a tilde. We then have \({{\widetilde{\mu }}_\mathrm{MLE}}= u_0\) and
where all equalities are understood point-wise, and \(\ell \) is the GLM anti-log-likelihood.
Proof
The MLE equation for the natural parameter of the saturated model is
Because \({{\widetilde{\theta }}_\mathrm{MLE}}\) and \({{\widetilde{\mu }}_\mathrm{MLE}}\) are in convex duality, they satisfy \({{\widetilde{\mu }}_\mathrm{MLE}}= b^\prime ({{\widetilde{\theta }}_\mathrm{MLE}})\). This shows that \({{\widetilde{\mu }}_\mathrm{MLE}}= u_0\). Moreover, Eq. (1) allows writing the scaled difference in anti-log-likelihood between any predictive model \(\theta \) and the saturated model \({{\widetilde{\theta }}_\mathrm{MLE}}\) as:
Inserting Eq. (6), we directly recognize the definition of a Bregman divergence on the right-hand side. Finally, the duality between Bregman divergences, \(\mathrm B _b(\theta \parallel {{\widetilde{\theta }}_\mathrm{MLE}}) = \mathrm B _{b^\star }(\widetilde{\mu }_\mathrm{MLE} \parallel \mu )\), allows us to conclude by substituting \({{\widetilde{\mu }}_\mathrm{MLE}}\) with \(u_0\). \(\square \)
This result also illustrates the meaning of the saturated model. First, the MLE of the average intensity is the image itself, illustrating the interpolating nature of the saturated model. Second, the saturated model normalizes the likelihood: The Bregman divergence is positive and zero at the saturated model parameter value \({{\widetilde{\theta }}_\mathrm{MLE}}\) or \(\widetilde{\mu }_\mathrm{MLE}=u_0\). Finally, the loss in fitting accuracy of the reduced model compared to the saturated model is quantified by an information measure, the Bregman divergence.
We can hence derive from \(\mathcal{E }_\mathrm{d}^\mathrm{{GLM}}\) (cf. Eq. 4) two equivalent data-fitting energies \(\mathcal{E }_\mathrm{d}^\mathrm{{B}}\) based on Bregman divergences. The likelihood of the saturated model acts as a normalization constant and will hence play no role in estimating the model parameter. Therefore, we can defineFootnote 8:
Result 1 allows us to rewrite this using a Bregman divergence, either in the natural parameter form
or in the mean parameter form
The last expression is the most informative from a modeling point of view, as the mean \(\mu \) is the direct target of the GLM. Table 1 shows the Bregman energy (9) for different noise models. Due to the equivalence of the GLM and Bregman energies, we omit from now on the superscript in the data-fitting energy.
To summarize, we have shown that there exists a duality between data-fitting energies derived from GLM statistical forward models and the Bregman divergence information criterion. This duality interprets the data-fitting energy as quantifying the information compression between the predictive model defined by the linear predictor \(\eta \) and the non-informative saturated model.
2.4 The GLM/Bregman-\(\text{ TV}_{{w_b}}\) model
The previous subsections were devoted to designing and analyzing new data-fitting energies that combine several image-processing tasks with image segmentation. As discussed in the introduction, the model needs to be completed with a regularizer. Regularization functionals are not the main topic of this paper. We hence consider only geometric priors and use one of the most frequently used regularizers for active contours, the geodesic length penalty (Caselles et al. 1997). It consists of a weighted length of the interface separating the foreground from the background region. Bresson et al. (2007) reformulated this prior using weighted total variation semi-norms \(\text{ TV}_{{w_b}}\):
where \(\varGamma \) is the (not necessarily connected) boundary of the domain \(\varOmega \) and \({w_b}\) is a positive boundary weight function known a priori and not to be confused with the data weights \(w_d\).
Combining the mean-parametrized Bregman divergence data-fitting energy (9) with the geodesic length prior (10), the full model considered here reads:
The scale parameter \(\phi \) has been absorbed into the regularization parameter \(\lambda \). As this is a segmentation model, both the foreground region \(\varOmega \) and the photometric parameters \(\varvec{\beta }\) are explicit arguments of the energy functional. The \(\varOmega \)-dependence enters \(\mathcal{E }_d\) only through the linear predictor \(\eta ({{\varvec{x}}},\varOmega ,\varvec{\beta })= \varvec{X}({{\varvec{x}}},\varOmega )^{T}\varvec{\beta }(\varOmega )\).
To summarize, we list the different ingredients of our image model and indicate which terms can be used to couple certain restoration task with segmentation. The REF noise model is entirely determined by the function \(b^\star \). The a priori given weights \(w_d\) and \({w_b}\) can be used to incorporate prior knowledge from a preprocessing step. The \(w_d\) can be used to indicate regions of the image were data are missing or uncertain. They thus encode a (TV-)inpainting task. The same weights can also be used to down-weight outliers identified by pre-filtering the image (Leung and Osher 2005). Similarly, \({w_b}\) can be used to enhance edge detection by driving the active contour to low-value regions of an edge map (Caselles et al. 1997). The link function \(g\) is usually the identity and, to the best of our knowledge, a possible non-linearity that has not yet been considered in image segmentation. It could, however, be used to linearize a non-linear problem or to enforce parameter constraints. The design matrix \(\varvec{X}\) can be used to encode prior information about spatial correlations between pixel values using a kernel \(\mathrm{K}\), as for example in the case of deconvolution, where \(\mathrm{K}\) is the PSF of the imaging system.
3 Inverse Problem Algorithms
In the previous section we have formulated a flexible forward model that combines image restoration with piecewise-constant segmentation. We now provide efficient algorithms for solving the resulting inverse problems. We limit ourselves to two regions only for the geometric inverse problem, because the algorithms and the convex relaxation considerations are qualitatively different when considering more than two regions (see Paul et al. 2011, for an extension of the geometric solver to multiple regions). The inverse problem is solved by minimizing the energy (11). This is a composite minimization problem consisting of a vector optimization problem for the photometric estimation and a geometric optimization problem for the segmentation.
3.1 Alternating Minimization
Alternating minimization (AM) is a classical and simple scheme for solving composite minimization problems (see e.g., Chan and Shen 2005). In image segmentation, this strategy is often used to sequentially solve the photometric and the geometric problem. In the following, we provide the details of an algorithm that can be used to solve the inverse problem associated with the present image model. The region statistics solver (RSS) is described in Sect. 3.2, and the algorithms used to solve the geometric inverse problem are described in Sect. 3.3. We propose two different geometric solvers, depending on the convexity of the problem.
3.2 Region Statistics Solver
We provide a unified way of solving the photometric inverse problem using a modification of Newton’s method. This section gathers results from the statistics literature and adapts them to our image processing problem. For the reader’s convenience we provide in the online appendix detailed proofs of the classical GLM results, which we adapted from the statistics literature to our framework.
3.2.1 Score Vector, Fisher Information Matrix, and the Maximum Likelihood Estimator \({\widehat{\varvec{\beta }}_\mathrm{MLE}}\)
We first introduce the quantities involved in deriving the Fisher scoring algorithm with the sign convention of an energy formulation. The maximum likelihood estimator (MLE) is the vector \({\widehat{\varvec{\beta }}_\mathrm{MLE}}\) satisfying the Euler-Lagrange equation for the log-likelihood. In statistics, the derivative with respect to \(\varvec{\beta }\) of the log-likelihood is called the score vector \(\varvec{s}\), and the associated Euler-Lagrange equation is called the score equation:
It is unaffected by sign changes, and we define here the score as the gradient of the energy (11) with respect to \(\varvec{\beta }\). This is the same definition as used in the statistics literature, up to a sign change. The score vector of a GLM is a well-known quantity (Nelder and Wedderburn 1972; McCullagh and Nelder 1989). We derive the local score \(\varvec{s}(\varvec{\beta },{{\varvec{x}}})\,{:=}\, \frac{\partial \ell }{\partial \varvec{\beta }}({{\varvec{x}}},\varvec{\beta })\) and extend it to the whole image under mild regularity conditions. Specifically, we need \(\ell \) to be regular enough to be able to swap derivation and integration.Footnote 9
Result 2
The GLM local score function is:
with \(W({{\varvec{x}}},\varvec{\beta })= \left( \sigma ^2({{\varvec{x}}},\varvec{\beta })g^{\prime }(\mu ({{\varvec{x}}},\varvec{\beta }))^2 \right) ^{-1}\). Under mild regularity conditions the whole-image score is:
Proof
It is a classical result for GLMs (McCullagh and Nelder 1989) that
The regularity condition allows interchanging derivation and integration, hence:
\(\square \)
The RSS is based on the Fisher information matrix, defined as the variance-covariance matrix \(\mathcal{I }\) of the score vector \(\varvec{s}\) and calculated as shown in the following Result.
Result 3
The Fisher information matrix of the score vector (13) is:
Similarly, under mild regularity conditions, the whole-image Fisher information matrix is
3.2.2 Fisher Scoring Algorithm
In GLMs (McCullagh and Nelder 1989), the score Eq. (12) is solved numerically using an iterative algorithm based on a modified Newton-Raphson method called Fisher scoring. The modification consists in replacing the negative Hessian of the score vector (called the observed information matrix) by its average, the Fisher information matrix. After iteration \(r\), one Fisher scoring iteration then reads:
The Fisher scoring algorithm is usually written as an Iteratively re-weighted least squares (IRWLS) algorithm. We rephrase this result and explicitly show the iterations for a two-region segmentation problem.
Result 4
The Fisher scoring iteration defined in (15) is equivalent to:
where
is called the adjusted dependent variable, i.e., the linearized form of the link function at the data \(u_0({{\varvec{x}}})\).
For a two-region segmentation problem with deconvolution (convolution operator being \(\mathrm{K}\)), one IRWLS iteration reads:
where the inverse Fisher information matrix is
and for \(i\in \{1,2\}\):
and for \((i,j)\in \{1,2\}\):
At convergence, the inverse Fisher information matrix provides a plug-in estimate of the asymptotic variance-covariance matrix of the estimated parameters \({\widehat{\varvec{\beta }}_\mathrm{MLE}}\):
Formulating Fisher scoring as an IRWLS problem admits a straightforward implementation of the RSS, requiring only a least-squares solver for Eq. (16) at each iteration of the IRWLS. For a two-region problem, the RSS is even simpler, as we only need to iterate (17) until a stopping criterion is met. The estimated variance-covariance matrix of \({\widehat{\varvec{\beta }}_\mathrm{MLE}}\) (18) gives asymptotic confidence intervals for the parameters and enables inference about the photometric vector \(\varvec{\beta }\).
One important case can be solved analytically and the MLE is hence found in one iteration: the Chan-Vese model with and without deconvolution with the identity link function. Without deconvolution, we recover the classical result by Chan and Vese (2001) that \({\widehat{\varvec{\beta }}_\mathrm{MLE}}\) contains the average foreground and background intensities. With deconvolution, we recover the result derived by Jung et al. (2009).
3.3 Geometric Solvers
The geometric inverse problem associated with the segmentation task is addressed differently depending on the convexity of the energy functional (11). If the energy is non-convex, we use a steepest descent approach (Sethian 1999; Osher and Fedkiw 2003). This requires deriving the shape gradient of the energy (11). The main difficulty hereby is that the regions are represented by masks amounting to hard membership functions. Deriving a gradient requires defining a functional derivative with respect to a domain. The set of image regions, however, does not have the structure of a vector space, requiring us to resort to the concept of a shape gradient (Aubert et al. 2003). This is then used to drive a surface, the active contour, to a local minimum of the energy. We choose a level-set representation of the active contour in order to formulate an algorithm that works in both 2D and 3D, and allows topology changes during contour evolution (see e.g. Aubert et al. 2003; Burger and Osher 2005; Osher and Fedkiw 2003; Sethian 1999). We derive the shape gradient of our energy using basic shape-derivative tools, introduced in image processing by Aubert et al. (2003). The resulting speed function can then be used in any level-set solver.
If the energy function (11) is convex, it has recently been shown (Chan et al. 2006; Bresson et al. 2007) that also the geometric inverse problem can be made convex by convex relaxation of the solution space. The solution space here is the set of binary functions (i.e., the masks), which is not convex. Relaxing it to the set of soft membership functions taking values in the interval \(\mathopen {[}0 \mathclose {}\mathpunct {}, 1\mathclose {]}\), however, renders the problem convex. Any convex optimizer can then be used to solve the problem. What remains is to study the relationship between the solution of the original non-convex problem and the convexified problem. For two-region segmentation, it has been shown that the convex relaxation is exact, in the sense that the globally optimal solution of the original non-convex problem can be obtained from the solution of the convex problem by simple thresholding (Chan and Esedoḡlu 2005; Burger and Hintermüller 2005; Chan et al. 2006; Bresson et al. 2007). We extend this result in two directions: First, we study in Sect. 3.3.2 the exactness of the convex relaxation for linear kernels \(\mathrm{K}\). We show that in general, the convex relaxation is not exact. Second, we derive a simple a posteriori upper bound on the energy difference between the thresholded solution of the convex problem and the global solution of the original non-convex problem. As a convex optimization algorithm, we adapt and improve the popular alternating split-Bregman (ASB) solver (Goldstein and Osher 2009; Goldstein et al. 2010; Setzer et al. 2010).
For the sake of simplicity, we consider in this section only two-region segmentations with \(\mathrm{K}\) representing a convolution (see e.g. Chan and Shen 2005, for classical mathematical hypotheses on convolution operators). The extension to multiple regions of the ASB has been described elsewhere (Paul et al. 2011). By convention we denote the foreground region \(\varOmega \,{:=}\,\varOmega _2\) and its mask \(M({{\varvec{x}}})\,{:=}\, M_2({{\varvec{x}}})\). The piecewise-constant object model can therefore be written as \(u({{\varvec{x}}})= (\beta _2-\beta _1)M({{\varvec{x}}})+\beta _1\), such that for fixed \(\varvec{\beta }\) it is a linear functional of \(M\) only.
3.3.1 Shape Gradient of the GLM/Bregman Energy
Aubert et al. (2003) introduced shape gradients to image processing as an analytical tool to derive speed functions for gradient-based geometric solvers. The active contour is then driven by a velocity field \(v_d+\lambda v_r\), where \(v_d\) and \(v_r\) are derived from the data-fitting and the prior energy, respectively. The velocity field \(v_r\) for TV regularizers is classical and not re-derived here (see e.g. Aubert et al. 2003).
Before stating the main result, we recall the Eulerian derivative of a domain functional and the shape derivative of a function. In order to define a derivative with respect to a domain, the speed method introduces a smooth auxiliary velocity field \(\varvec{V}\), driving the following initial-value problem:
The solution of this differential equation is a flow denoted \(T(t,{{\varvec{x}}})\). It transforms any initial point x in \({{\varvec{x}}}_t \,{:=}\, T(t,{{\varvec{x}}})\) and any domain \(\varOmega \) in \(\varOmega _t \,{:=}\, \left\{ {{\varvec{x}}}_t \mid {{\varvec{x}}}\in \varOmega \right\} \). A perturbation of \(\varOmega \) is then formalized as the infinitesimal action of \(\varvec{V}\)on \(\varOmega \) around \(t=0\), still denoted by \(\varvec{V}({{\varvec{x}}}) \,{:=}\, \varvec{V}(0,{{\varvec{x}}}) = \left. \frac{\partial T_t}{\partial t}\right| _{t=0}\).
Definition 1
The Eulerian (or Gâteaux) derivative of the domain functional \(\mathcal{E }(\varOmega )\) in direction \(\varvec{V}\) is:
The shape derivative of the function \(f(\varvec{x},\varOmega )\) is:
Result 5
Assume that \(\ell ({{\varvec{x}}},\varOmega )\) is integrableFootnote 10 and that the velocity fields \({\left\{ \varvec{V}(t,\cdot )\right\} }_{t\in \mathopen {[}0 \mathclose {}\mathpunct {}, T\mathclose {[}}\) are regularFootnote 11 enough to render the shape derivative \(\ell _s({{\varvec{x}}},\varOmega ;\varvec{V})\) and the functions \({{\varvec{x}}}~\mapsto \ell ({{\varvec{x}}},\varOmega _t)\) integrable. Then, the Eulerian derivative in direction \(\varvec{V}\)of the data-fitting energy (4) exists and is given by:
where \(\varvec{s}(\varOmega ,\varvec{\beta };\varvec{V}) \,{:=}\, \int _{\varOmega _I}\varvec{s}_s({{\varvec{x}}},\varOmega ;\varvec{V})\mathrm{d}{{\varvec{x}}}\), the geometric score vector \(\varvec{s}_s({{\varvec{x}}},\varOmega ;\varvec{V})\) being defined as:
If the MLE estimator \({\widehat{\varvec{\beta }}_\mathrm{MLE}}\) is used, this simplifies to:
Proof
To simplify notation, we introduce the shorthand \(f(t) \,{:=}\, \ell ({{\varvec{x}}},\varOmega _t)\), where the dependence in x is implicit. Integration is always with respect to x, and we write \(\int f(t)\) instead of \(\int _{\varOmega _I}\ell ({{\varvec{x}}},\varOmega _t)\mathrm{d}{{\varvec{x}}}\).
The first step is to prove that
By assumption, the quantities \(f(t), \,f(0) \,{:=}\, \ell ({{\varvec{x}}},\varOmega )\), and \(f^\prime (0)\,{:=}\, \ell _s({{\varvec{x}}},\varOmega ;\varvec{V})\) exist and are integrable. We now introduce a sequence \(t_n>0\) in \(\mathopen {[}0 \mathclose {}\mathpunct {}, T\mathclose {[}\) converging to zero. In terms of \(f\), Eq. (19) amounts to proving that \(\forall \epsilon > 0\) there exists a rank \(N\) such that \(\forall n \ge N, \,\left|\int t^{-1}(f(t_n)-f(0))-f^\prime (0)\right|\) is bounded by \(\epsilon \). The existence of \(f^\prime (0)\) implies that for almost all \({{\varvec{x}}}\) and all \(\epsilon ^\prime >0\), we can find \(N^\prime \) after which \(\left|t^{-1}(f(t_n)-f(0))-f^\prime (0)\right|\) is uniformly bounded in x by \(\epsilon ^\prime \). Picking \(\epsilon ^\prime = \left|{\varOmega _I}\right|^{-1}\epsilon \), and integrating the former bound, we can find a rank \(N=N^\prime \) after which \(\int _{\varOmega _I}\left|t^{-1}(f(t_n)-f(0))-f^\prime (0)\right|\) is bounded by \(\epsilon \). To conclude, we use that for any \(t_n\),
This shows (19).
Computing the Eulerian derivative amounts to computing \(\ell _s({{\varvec{x}}},\varOmega ;\varvec{V})\). We use the chain rule \(\frac{\mathrm{d}}{\mathrm{d}t} \ell ({{\varvec{x}}},\varOmega _t) = \frac{\partial \ell ({{\varvec{x}}},\varvec{\beta })}{\partial \eta } \frac{\mathrm{d}\eta (\varOmega _t)}{\mathrm{d}t}\). We know from Eq. (13) that:
The chain rule again provides:
Taking \(t \rightarrow 0\) and using Definition 1, this becomes:
Combining the previous calculations and evaluating at \(t=0\), we obtain the first part of result 5. By definition of \({\widehat{\varvec{\beta }}_\mathrm{MLE}}, \,\varvec{s}(\varOmega ,{\widehat{\varvec{\beta }}_\mathrm{MLE}})=0\), and we obtain the second part of result 5. \(\square \)
At this stage, the speed function \(v_d\) is not explicit. We now specialize the previous result to the case of two-region segmentation with deconvolution.
Result 6
For a two-region segmentation problem with a convolution \(\mathrm{K}\), \(\left\langle \mathcal{E }^\prime _d(\varOmega ,{\widehat{\varvec{\beta }}_\mathrm{MLE}}), \varvec{V}\right\rangle \) reduces to
where the speed function \(v_d\) is
\(\Delta {\widehat{\varvec{\beta }}_\mathrm{MLE}}\,{:=}\,(\widehat{\beta _2}-\widehat{\beta _1})\) is the photometric contrast between foreground and background, and \(\mathrm{K}^{T}\)is the adjoint of \(\mathrm{K}\).
Proof
Under the stated assumptions, the design matrix is \(\varvec{X}({{\varvec{x}}},\varOmega ) = \mathrm{K}*1_\varOmega ({{\varvec{x}}}) \begin{bmatrix} 1,&-1 \end{bmatrix}^{T} + \begin{bmatrix} 0,&1 \end{bmatrix}^{T}\). Applying theorem 5.5 of Aubert et al. (2003) to \(f({{\varvec{x}}},\varOmega ) \,{:=}\, \mathrm{K}*1_\varOmega \),
we obtain \(\varvec{X}_s^{T}({{\varvec{x}}},\varOmega ,\varvec{V}) \varvec{\beta }= -(\beta _2-\beta _1) f_s({{\varvec{x}}},\varOmega ,\varvec{V}).\) Using result 5 and rearranging the order of the integrals, we obtain the result. \(\square \)
For a Gaussian noise model, we recover the known speed functions of the Chan-Vese model without (Chan and Vese 2001) and with (Jung et al. 2009) deconvolution.
3.3.2 Convex Relaxation
We study the convex relaxation of the set of binary functions to the set of soft membership functions. This section is not restricted to the class of data-fitting energies introduced in Sect. 2. It is valid for all energies that are convex in the linear predictor.
Exact convex relaxations of two-region segmentation (see Chan and Esedoḡlu 2005; Burger and Hintermüller 2005; Chan et al. 2006; Bresson et al. 2007) rely on the co-area formula \(\mathcal{E }(M) = \int _0^1 \mathcal{E }(\mathbf 1 _{M\ge t})\mathrm{d}t\), relating the energy of the mask \(M\) to the energy of its thresholded version \(\mathbf 1 _{M\ge t}\). Such a result holds for the total variation functional (10), and for all linear functionals due to the layer-cake formula (Chan and Shen 2005). In the class of energies we have introduced, a lack of exact convex relaxation can only be due to the data-fitting energy not being a linear functional in general. The regularization energy satisfies the co-area formula. We hence investigate the conditions under which a data-fitting energy involving a linear operator \(\mathrm{K}\) in the linear predictor satisfies a co-area formula.
Since the kernel \(\mathrm{K}\) defines a linear functional, the co-area formula holds and we have that for all x in \({\varOmega _I}\):
This can be interpreted as the expectation of the random variable \(\mathrm{K}\left[ \mathbf 1 _{M\ge T}\right] \!({{\varvec{x}}})\), with \(T\) a continuous random variable in \(\mathopen {[}0 \mathclose {}\mathpunct {}, 1\mathclose {]}\). The energy functional being convex by hypothesis, Jensen’s inequality applies:
or, written in \(M\) only:
A generalized co-area formula would correspond to an equality. Hence, the conditions for an equality in Eq. (20) are also the ones for a generalized co-area formula to hold: either \(\mathrm{K}\left[ \mathbf 1 _{M \ge t}\right] \!({{\varvec{x}}})\) is constant in \(t\) for almost all \({{\varvec{x}}}\in {\varOmega _I}\), or \(\mathcal{E }_\mathrm{d}\) is linear. This result shows that in general a (generalized) co-area formula does not hold for two-region segmentation. Therefore, an exact convex relaxation by thresholding does not exist.
Convex relaxation hence is exact if the soft mask only takes values in the set \(\left\{ 0,1\right\} \) x-almost everywhere. Put differently, if the mask resulting from the convex optimization problem is actually binary, a generalized co-area formula holds for the data-fitting energy and the global solution of the original non-convex problem is recovered. If the smooth mask is not binary, one can provide a rough error estimate in energy between a thresholded solution of the convex problem, \(M^\star \), and the global solution \(\mathbf 1 _{\Sigma ^\star }\) of the original non-convex problem. Here, \(\Sigma ^\star \) is the true segmentation. The set of soft membership functions taking values in \(\mathopen {[}0 \mathclose {}\mathpunct {}, 1\mathclose {]}\) is a superset of the set of binary functions. This inclusion entails that \(\mathcal{E }( M^\star ) \le \mathcal{E }(\mathbf 1 _{\Sigma ^\star })\). In addition, any thresholded version of \(M^\star \) is a binary function, and hence \(\mathcal{E }(\mathbf 1 _{\Sigma ^\star }) \le \mathcal{E }( \mathbf 1 _{M^\star \ge t})\). These two inequalities can be combined to an upper bound in energy valid for any threshold \(t\in \mathopen {[}0 \mathclose {}\mathpunct {}, 1\mathclose {]}\):
This bound is useful in two ways: First, it is an a posterioricertificate of the exactness of the convex relaxation. Second, it can be used to choose the threshold \(t\) as the one minimizing the upper bound on the relaxation error. The same upper bound has also been derived by Pock et al. (2009) as an error bound when the regularization energy fails to satisfy a co-area formula.
The second case in which an exact convex relaxation exists is for a linear energy. We now show that even for a non-convex data-fitting energy in \(\eta \), one can rewrite it prior to convex relaxation as a linear energy if \(\mathrm{K}\) is the identity. In this case, \(\mathcal{E }_\mathrm{d}\) is an integral of a function \(E\) of the binary mask and the photometric constants only: \(E\left( {{\varvec{x}}},\left( \beta _2-\beta _1\right) M({{\varvec{x}}})+\beta _1\right) \). The integrand hence is \(E({{\varvec{x}}},\beta _1)\) if \(M({{\varvec{x}}})=0\) and \(E({{\varvec{x}}},\beta _2)\) if \(M({{\varvec{x}}})=1\). After regrouping terms and excluding the mask-independent integral, we obtain a functional that is linear in \(M\):
Therefore, one can always rewrite the data-fitting energy as a linear functional if \(\mathrm{K}\) is the identity, even for a non-convex data-fitting energy. This reduces the problem to the classical segmentation model with a linear data-fitting functional and a total-variation regularizer, for which exact convex relaxations are known for two-region problems (see Burger and Hintermüller 2005; Chan et al. 2006; Bresson et al. 2007). We summarize the previous discussion in the following result.
Result 7
Consider two-region segmentation formulated as a geometric optimization problem over an energy written as the sum of a data-fitting energy \(\mathcal{E }_\mathrm{d}\) and a regularization energy \(\mathcal{E }_\mathrm{r}\). Assume that a generalized co-area formula holds for \(\mathcal{E }_\mathrm{r}\).
If \(\mathrm{K}\) is the identity, we can always rewrite \(\mathcal{E }_\mathrm{d}\) as a linear functional in \(M\) (22), for which an exact convex relaxation always exists. If \(\mathrm{K}\) is linear and \(\mathcal{E }_\mathrm{d}\) is convex in \(\mathrm{K}\!\left[ M\right] \), the “generalized co-area inequality” (20) holds and an exact convex relaxation by thresholding does not exist in general. If a global solution \(M^\star \) of the relaxed problem is binary, \(\mathbf 1 _{\Sigma ^\star }\) is a global solution of the original non-convex segmentation problem. If \(M^\star \) is not binary, the a posteriori upper bound (21) holds for any threshold \(t\).
3.3.3 A New ASB Scheme for Image Segmentation
In the previous section we discussed convex relaxation of image segmentation tasks coupled to image restoration, and we emphasized the role of the kernel \(\mathrm{K}\). In practice, an efficient algorithm for solving the relaxed convex problem is needed. While any convex optimization algorithm could be used, we choose the alternating split-Bregman (ASB) method as introduced for image segmentation by Goldstein et al. (2010) as a prototype. The contribution of this section is two-fold: First, we show how to rewrite the ASB algorithm in a form that decouples even further the different energy terms in the geometric optimization problem, as described in a more general context by Esser (2009) and Setzer et al. (2010). The second contribution is to provide a new algorithm based on the ASB framework.
Goldstein et al. (2010) proposed the ASB method for the globally convex active contour formulation of image segmentation:
where \(M\) is a soft membership function as explained in the previous section, \(\text{ TV}_{{w_b}}\) is the \({w_b}\)-weighted total variation norm (10), and \(v_d\) is the speed function of the data-fitting energy.
Consider how ASB works for problems written as the sum of two convex, lower semi-continuous (l.s.c.) and proper energies coupled in their argument via an operator \(\mathrm C \):
The first step of ASB is to introduce an auxiliary variable \(w\) in order to transform the unconstrained problem (24) to a constrained problem with \(w = \mathrm C \! M\). The constraint is imposed exactly by applying Bregman iterations (Goldstein and Osher 2009), so that one iteration of the ASB after iteration \(k\) reads:
where \(b\) is called the Bregman variable and \(\gamma > 0\) is the step size (Setzer et al. 2010; Setzer 2011). The optimization problem (25) is solved by alternating optimization, sequentially solving for \(M\) and \(w\). For convergence results about the ASB method, and its connections with other well-known convex optimization techniques, we refer to the works of Esser (2009) and Setzer (2011), and the references therein.
Goldstein et al. (2010) apply ASB with:
where \(\varvec{w}\) is a vector field and \(\left||\left|\varvec{w}\right|\right||_1\) is the \(L^1\) norm of the Euclidean norm of \(\varvec{w}\) under the constraint that \(\forall {{\varvec{x}}},\ M({{\varvec{x}}}) \in \mathopen {[}0 \mathclose {}\mathpunct {}, 1\mathclose {]}\). This renders the subproblem associated with \(M\) a constrained optimization problem:
Goldstein et al. (2010) propose to approximately solve this subproblem by one modified Gauss-Seidel iteration, where the constraint \(M\in \mathopen {[}0 \mathclose {}\mathpunct {}, 1\mathclose {]}\) is handled within Gauss-Seidel. This splitting hence results in a subproblem where two things are done simultaneously: solving the \(M\)-subproblem and handling the soft membership constraint.
Here we propose a different splitting of problem (23), where the constraint is handled in a separate subproblem. Therefore, we introduce the indicator functional of the set of soft membership masks from convex analysis, \(\iota _{\mathopen {[}0 \mathclose {}\mathpunct {}, 1\mathclose {]}}(M)\), as being \(0\) if \(M\in \mathopen {[}0 \mathclose {}\mathpunct {}, 1\mathclose {]}\) everywhere and \(\infty \) otherwise. The globally convex segmentation problem can then be written as the unconstrained convex problem:
The objective functional of (27) is a sum of convex, l.s.c., proper functionals coupled in their arguments. Setzer et al. (2010) propose a splitting that results in split-Bregman iterations with decoupled subproblems. Consider the sum of \(m\) convex, l.s.c. and proper functionals \({\left\{ \mathcal{F }_i\right\} }_{i = 1,\cdots ,m}\), coupled in their arguments by \(m\) operators \({\left\{ \mathrm C _i \right\} }_{i = 1,\cdots ,m}\): \(\mathcal{E }(M) = \sum _{i=1}^{m} \mathcal{F }_i(\mathrm C _i M)\). The ASB strategy is then applied to:
where we have emphasized with a bold font that \(\mathbf{C}\) and \(\varvec{w}\) are stacked quantities. The advantage of this splitting is that the \(M\)-subproblem is a least-squares one and the \(w\)-subproblem decouples and can be solved independently. We refer to the works of Esser (2009) and Setzer et al. (2010) for details in a pure image-restoration context and show below the details for joint segmentation/restoration.
The GLM/Bregman-\(\text{ TV}_{{w_b}}\) energy (11) can be rewritten with \(m=3\) and \(\mathbf{C} \,{:=}\, \begin{bmatrix} \mathrm{K},&\nabla ,&\mathrm Id \end{bmatrix}^{T}\) as:
The convex functional \(\mathcal{F }_1\) can be a GLM/Bregman data-fitting energy as presented here, or any other convex energy, such as a \(L^1\) fidelity term.

The geometric ASB solver for problem (28) is described in Algorithm 1. The variables used to enforce the constraints \(w_1, \,w_3, \,b_1\), and \(b_3\) are scalar fields, whereas \(\varvec{w}_2\) and \(\varvec{b}_2\) are \(d\)-dimensional vector fields with \(d\) the dimension of the image. All fields are discretized on the same pixel grid as the data and the mask \(M\). The two operators \(\mathrm{K}\) and \(\nabla \) assume homogeneous Neumann boundary conditions. We follow Chambolle (2004) for discretizing the gradient \(\nabla \), denoted D, and its adjoint \(\text{ D}^{T} := -\text{ div}\). The discretized functional \(\mathcal{F }_2\) is \(\mathcal{F }_2(\varvec{w}_2) = \left||\left|\varvec{w}_2\right|\right||_1\). It is the \({w_b}\)-weighted sum over the pixel grid of the Euclidean norm of \(\varvec{w}_2\) at each pixel. The step size \(\gamma \) is the only free parameter of the algorithm. We now describe how each subproblem is solved.
Solution of subproblem (29)
The Euler-Lagrange equation of the least squares problem (29) after regrouping the terms in \(M\) is:
with \(A=(\mathrm{K}^{T}\mathrm{K}+\mathrm D \!\text{ D}^\mathrm{T} \!+ \text{ Id})\). This linear system can efficiently be solved using a spectral solver, since the operator \(A\) can be diagonalized with a fast discrete cosine transform (DCT-II), as explained by Strang (1999) (see Tai and Wu 2009, for the introduction of an FFT-based method in the context of split-Bregman algorithms). An implementation based on fast Fourier transforms (FFT) can solve this system in \(O(N_p\log N_p)\) operations, where \(N_p\) is the total number of pixels.
Solution of subproblem (30)
The Euler-Lagrange equation for subproblem (30) is:
where \(v_d\) is the gradient of \(\mathcal{F }_1(w_1)\). Equation 33 is in general non-linear in \(w_1\), but solutions can be approximated numerically. For the data-fitting energy presented here, its form is similar to the speed function in result 6. Contrary to the shape gradient approach, classical variational calculus allows finding \(v_d\) for the GLM energy. The derivation is similar to the one for the shape gradient and we do not reproduce it there. We simply state the result:
which is similar to the formula in result 6, except that the kernel \(\mathrm{K}\) is not present, due to the splitting via \(w_1\). This means in particular that \(\mu \) is defined as \(g(\mu ({{\varvec{x}}},\varvec{\beta })) = \Delta \varvec{\beta }\, w_1({{\varvec{x}}})+\beta _1\). For practically important cases, Eq. 33 can be solved analytically. In the online appendix, we provide the analytical solutions of (30) for GaussianFootnote 12, Poisson, and Bernoulli noise models with an identity link function.
Solution of subproblem (31)
Subproblem (31) is a \(L^1-L^2\) optimization problem for which the exact solution is known analytically. The solution is found by coupled thresholding (see Goldstein and Osher 2009, and references therein):
with \(\varvec{c} = \mathrm D \! M^{k+1}+\varvec{b}_2^k\) and \(\left|\cdot \right|\) the Euclidean norm.
Solution of subproblem (32)
Subproblem (32) is the orthogonal projection of \(b_3^k+M^{k+1}\) onto the interval \(\mathopen {[}0 \mathclose {}\mathpunct {}, 1\mathclose {]}\), whose solution is:
4 Experimental Results
We define the signal-to-noise ratio (SNR) as used in microscopy. For an object of mean intensity \(\mu _2\) observed over a background of mean intensity \(\mu _1\) and distorted by centered additive Gaussian noise of variance \(\sigma ^2\), the SNR is defined as the ratio between the intensity contrast, \(\mu _2-\mu _1\), and the standard deviation of the noise, \(\sigma \). As we want to compare different noise distributions, we measure the SNR in a distribution-independent way. Following Goudail et al. (2004), we base our definitionFootnote 13 on the Bhattacharyya distance \(\mathcal{B }\): \({\mathrm{SNR}}\,{:=}\,\sqrt{8\mathcal{B }}\).
4.1 GLM/Bregman Model Expressivity
We present a series of calibrated experiments that illustrate both aspects of the present work: the forward model coupling image segmentation with image restoration (Sect. 2) and the associated inverse problem (Sect. 3). For the first set of experiments, we use a synthetic noiseless (\(166\times 171\) pixels) binary image composed of four shapes known to be hard for image segmentation: a ring creating local minima in the energy, a U-shaped object where the concavity presents difficulties to local iterative solvers, a square where the sharp corners are difficult to reconstruct, and a triangle with edges not aligned with the image axes, which is problematic for methods based on anisotropic regularizers.
Different forward models are used to simulate different perturbations to this noiseless binary image. We consider four noise models from the REF: Gaussian, Poisson, Bernoulli, and gamma noise. In addition, we consider Laplace noise, which is not in the EF. Our choice of EF members is justified as follows: The Gaussian, Poisson, and Bernoulli models result in convex energies if the identity link function is used, whereas the gamma noise model results in a non-convex energy. Moreover, the variance functions scale differently for these noise models, resulting in qualitatively different denoising tasks. The variance functions are constant (Gaussian, \(V(\mu ) = 1\)), linear (Poisson, \(V(\mu )=\mu \)), and quadratic (Bernoulli \(V(\mu ) = \mu (1-\mu )\) and gamma \(V(\mu ) = \mu ^2\)). The SNR is fixed at \({\mathrm{SNR}}~= 4\) for all images, corresponding to \(\mathcal{B }= 2\). The background intensity \(\beta _1\) is fixed (see Fig. 1 for the specific values) and the foreground intensity \(\beta _2\) is determined to match the prescribed SNR. The binary mask \(M\) is then transformed into a piecewise-constant image using Eq. (5).
Coupling image segmentation with image restoration using the GLM/Bregman-\(\text{ TV}_{{w_b}}\) model. Nuisance parameters are fixed as follows: the scale parameter of Gaussian and Laplace distributions is 1. Gamma noise is of order 15. The blurring kernel \(\mathrm{K}\) is a Gaussian of standard deviation 2 pixels. The inpainting mask is the same for all images and corresponds to removing \(\sim \)20 % of the pixels in random disks. Final segmentations from the level-set solver (LSS) and the alternating split-Bregman solver (ASBS) are shown along with the number of iterations \(N_\mathrm{iter}^\star \) and the final energy \(\mathcal{E }^\star \). Photometric constants are re-estimated every 150 iterations until the relative error in energy is below \(10^{-6}\). The maximum number of iterations allowed is 1,500. Both algorithms are always initialized with the same binary mask, an array of disks
In order to illustrate the coupling of segmentation with deconvolution and inpainting, we generate for each noise model blurred images and images with missing data as given by an inpainting mask. Blurring is done with an isotropic, homogeneous Gaussian kernel \(\mathrm{K}\) applied to the piecewise-constant image \(u\). Either \(u\) or its blurred version is then used as the mean of the distribution for each noise. The values of all arameters can be found in the caption of Fig. 1. A set of noisy images is generated for each combination, resulting in 10 noisy images (columns 1 and 7 in Fig. 1). The inpainting mask is the same for all experiments and is generated randomly once. This results in another 10 noisy images (columns 4 and 10 in Fig. 1). Before solving the inverse problem, all images are normalized between 0 and 1. For each image, alternating minimization (AM) is used based on either a level-set solver (LSS) or the alternating split-Bregman solver (ASBS) given in Algorithm 1. The total number of iterations allowed is 1500 in all cases. The algorithms stop before if the relative decay in energy between consecutive iterations falls below \(10^{-6}\). During AM, each subproblem is solved exactly. We hence fix the number of iterations before re-estimating the photometric constants to a large value, here 150. For both algorithms, the initial mask is a set of densely covering circles. The regularization parameters are found manually and set to \(\lambda = 0.1\) for all experiments, except for gamma and Bernoulli noise (\(\lambda _\mathrm{gamma} = 5\) and \(\lambda _\mathrm{Bernoulli}=3\)). The step size \(\gamma \) for ASBS is set to \(\gamma = 0.1\) for all experiments. For each experiment, the final energy of the segmentation, \(\mathcal{E }^\star \), along with the total number of iterations required to reach it, \(N_\mathrm{iter}^\star \), is reported below the image showing the final joint segmentation/restoration.
Figure 1 illustrates the expressivity of the model described in Sect. 2. The results presented in Sect. 3 allow solving coupled segmentation/restoration problems using either level-set solvers (Sect.3.3.1) or convex relaxation with the ASB scheme (Sects. 3.3.2 and 3.3.3). In all cases we observe that the ASBS finds better solutions (in energy) in less iterations than the LSS. Even though not all photometric/geometric inverse problems are jointly convex (but at most separately convex), we observe that the convex relaxation approach yields solutions close to the ground truth. For example, we observe that for most of the LSS results the inner circle is almost never found by the algorithm, whereas the ASBS always finds it. Detailed optimization trajectories for Fig. 1a4, a10 can be found in the online appendix.
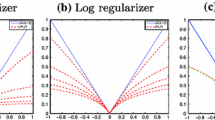
4.2 Threshold Selection Using (21)
When an exact convex relaxation exists (see Sect. 3.3.2), the thresholding parameter can be chosen quite arbitrarily, and is usually set to \(t=0.5\). In case the convex relaxation is not exact, we propose to use the a posteriori upper bound (21) to select the threshold.
To illustrate the effect of this selection procedure, we design a second test case. The task is to segment a U shape close (4 pixels separation) to a square of similar dimensions (\(50 \times 50\) pixels). The piecewise-constant ground-truth image (Fig. 2a) is corrupted with Gaussian noise (SNR=4) before (Fig. 2b) and after convolution with an isotropic, homogeneous Gaussian kernel of standard deviation \(2\) pixels (Fig. 2c).
Threshold selection using the a posteriori error upper bound (21). (a) Ground-truth image (\(\beta _1=10\) and \(\beta _2=14\)). (b) Ground-truth image (a) corrupted with additive Gaussian noise (SNR = 4). (c) Blurred (isotropic Gaussian, standard deviation \(\sigma =2\) pixels) ground-truth image corrupted with additive Gaussian noise (SNR = 4). (d–f) Final masks obtained from applying the ASBS to (b) with \(\lambda =0.1\) (d), to (c) with \(\lambda =0.075\) (e), and to (c) with \(\lambda =0.125\) (f). Panels (g–i) show the error upper bound (solid blue line, left axis) and the MCC (solid red line, right axis) as a function of the threshold \(t\). Gray shaded regions correspond to threshold values resulting in the correct topology. Optimal (g2, h2, and i2) and suboptimal (g1,3, h1,3, and i1,3) segmentations are shown below
Without deconvolution convex relaxation is exact, and the result from the ASBS is almost binary (Fig. 2d). With deconvolution, however, convex relaxation is not exact, and the result from the ASBS is not binary (Fig. 2e, f). For each mask 2d–f the a posteriori error bound (21) is shown as a function of the threshold \(t\) (Fig. 2g–i). Knowing the ground-truth segmentation (Fig. 2a), we assess the quality of the binary classification resulting from the segmentation for different thresholds. We use the Matthews correlation coefficient (MCC) (Matthews 1975; Baldi et al. 2000) (solid red line) as quality measure. The MCC correlates the observed classification to the predicted one, and is normalized between 0 and 1: a value close to 1 represents perfect classification and a value close to 0 corresponds to an average random prediction.
In the case of exact convex relaxation, the a posteriori upper bound is relatively small for almost all thresholds (Fig. 2g) and quite insensitive to the actual value of the threshold. The optimal threshold (marked g2) and its associated segmentation (Fig. 2g2) are shown along with segmentations corresponding to an upper bound 1.5 times larger than optimal (Fig. 2g1, g3). The two suboptimal segmentations g1 and g3 are very close to ground truth and differ from it only by a few pixels; the topology is always correct. This robustness is reflected in the MCC saturating at 1.
In the case of approximate convex relaxation (Fig. 2h–i), the a posteriori upper bound is higher than for exact convex relaxation (Fig. 2h, h2, i, i2). We observe that the MCC is negatively correlated with the a posteriori upper bound, and that the threshold corresponding to the minimum upper bound corresponds to the maximum MCC. The difference between Fig. 2h, i is the regularization parameter used. Similarly to the exact convex relaxation case, we select suboptimal segmentations (h1, h2, i1, and i2). For lower regularization (\(\lambda =0.075\)), the optimal segmentation (h2), lies in the gray shaded region of correct topology (Fig. 2h, h2). Between the suboptimal segmentation h1 and the optimal h2, we observe a kink in the error bound, corresponding to the loss of separation between the two objects (compare h1 and h2), as driven by the regularization energy. For a larger regularization parameter (\(\lambda =0.125\)), the kink appears to the right of the optimal segmentation, between i2 and i3. In this case, the optimal segmentation i2 does not reconstruct the correct topology. It is important to note that this comes from the model attributing more or less weight to the regularization energy. This is reflected in the soft labeling functions, where the values between the two objects are lower for the smaller regularization coefficient (Fig. 2e) than for the larger one (Fig. 2f).
4.3 Tradeoff Between Speed and Accuracy
We investigate the influence of the step size \(\gamma \) and the photometric re-estimation period \(\tau _\beta \) on the final energy \(\mathcal{E }^\star \) and the number of iterations \(N_\mathrm{iter}^\star \) needed to reach a relative difference in energy below machine precision. We use the synthetic image introduced in Sect. 4.1, blurred with a Gaussian kernel of standard deviation 2 pixels and corrupted with Gaussian noise of SNR \(=4\). The same inpainting mask as in Fig. 1 is used. We set the regularization parameter to \(\lambda =0.1\) as in the previous experiments. We conduct 1435 independent experiments with the step size \(\gamma \) ranging in \(\mathopen {[}0.005 \mathclose {}\mathpunct {}, 1\mathclose {]}\) and the photometric re-estimation period \(\tau _\beta \) in \(\mathopen {[}1 \mathclose {}\mathpunct {}, 50\mathclose {]}\). For each experiment we report the final energy \(\mathcal{E }^\star \) after optimal thresholding, the number of iterations \(N_\mathrm{iter}^\star \) required for the relative error to drop below machine precision, and the CPU time in seconds. The algorithm is implemented in pure Matlab and all experiments are performed on a 2.8 GHz Intel Xeon E5462 CPU. Across all experiments, we measure a median time per iteration of \(6.8\times 10^{-2}\) s.
Figure 3 summarizes the results. We observe a tradeoff between the final energy \(\mathcal{E }^\star \) and the number of iterations \(N_\mathrm{iter}^\star \). The lower-left region C of the scatter plot contains parameter combinations corresponding to optimal tradeoffs between accuracy and speed. In order to get a qualitative feeling for how the two parameters influence the tradeoff, the inset in Fig. 3 shows the dependence of the final energy \(\mathcal{E }^\star \) on the step size \(\gamma \) for the points in the shaded band around \(N_\mathrm{iter}^\star \approx 100\). We observe a positive linear correlation between \(\gamma \) and \(N_\mathrm{iter}^\star \). The influence of the photometric re-estimation period is trivial and hence not shown: the longer the re-estimation period, the larger the total number of iterations. For a more quantitative picture, we report in Table 2 the median values of the parameters of the ASBS in the four regions A–D indicated in Fig. 3. We observe that both parameters are positively correlated with both \(\mathcal{E }^\star \) and \(N_\mathrm{iter}^\star \).
Tradeoff between speed and accuracy in the ASBS. The main plot shows the final energy \(\mathcal{E }^\star \) and the number of iterations \(N_\mathrm{iter}^\star \) taken to reach the stopping criterion (relative energy drop below machine precision) for various combinations of the step size \(\gamma \) and the photometric re-estimation period \(\tau _\beta \). Regions A–D corresponding to Table 2 are shown. The inset figure shows the linear correlation between the step size \(\gamma \) and the final energy for the data points in the shaded band around \(N_\mathrm{iter}^\star \,{\approx }\,100\)
4.4 Comparison with Goldstein et al. (2010)
Goldstein et al. (2010) adapted the ASB algorithm to the Chan-Vese model (Chan and Vese 2001). Our ASB formulation uses a different splitting (see Sect. 3.3.3). We compare the two algorithms using the “cameraman” image corrupted with Gaussian noise of SNR=4 (Fig. 4a,b). The goal is not to assess which formulation is better in general, but to emphasize the influence of the splitting scheme on both solution quality and algorithmic efficiency. In order to compare the two algorithms we parametrize the ASB algorithm of Goldstein et al. (2010) in a way similar to our algorithm (see Eq. 26) and implement it in our AM solver code.
Comparison of the ASB algorithm by Goldstein et al. (2010) with Algorithm 1. The noiseless image (a) is corrupted with Gaussian noise (SNR \(=\) 4) (b). We show the segmentations obtained with the ASB of Goldstein et al. (2010) (c) and Algorithm 1 (d) for \(\lambda =0.1, \,\tau _\beta =15\), and \(\gamma =2\). Panel (e) shows the energy traces of Goldstein’s algorithm (blue) and Algorithm 1 (red). The inset shows the energy traces for \(\gamma =0.2\)
For both algorithms we use a regularization parameter of \(\lambda =0.1\), a step size of \(\gamma = 2\), a photometric update period of \(\tau _\beta =15\), and an Otsu-thresholded image as initialization. The resulting segmentations from the two algorithms are visually similar (Fig. 4c for Goldstein et al. (2010) and Fig. 4d for the present algorithm). Also the final energies reached by the two algorithms are comparable (Fig. 4e). However, we observe that the present ASB formulation decreases the energy faster than the one of Goldstein et al. (2010) and terminates earlier. Moreover, it reaches a slightly lower energy, resulting in minute differences in the segmentation, e.g., around the ear of the cameraman. Since a smaller step size is expected to lead to lower-energy solutions (see Sect. 4.3), we run both algorithms with a smaller \(\gamma \) and find that this increases the discrepancy between the two algorithms: the initial energy decrease of the present algorithm seems almost unaffected by the step size, although it takes longer to converge. In the formulation of Goldstein et al. (2010), a smaller step size slows down the decay in energy.
We have included the reference ASB of Goldstein et al. (2010) in our Matlab code in order to also compare the CPU times of both algorithms. The present algorithm segments the cameraman image in 45 s. The ASB of Goldstein et al. (2010) finds a local minimum in 64 s. The present ASBS requires 0.60 s per iteration, that of Goldstein et al. (2010) only 0.33 s per iteration. The formulation of Goldstein et al. (2010) requires storage for \(\text{2d+1}\) arrays of the size of the \(d\)-dimensional image. The present formulation requires \(\text{2d+5}\) arrays of the size of the image, due to the two additional splittings. The different per-iteration times can be explained as follows: Goldstein et al. (2010) exploit the fact that solving the subproblems in an ASB scheme approximately does not impair the convergence of the overall algorithm. They thus use only one iteration of a Gauss-Seidel solver with projection to solve the \(M\)-subproblem. We use an FFT-based spectral solver, which solves the subproblem exactly. One iteration of our ASBS is hence more expensive, but exactly solving all subproblems decreases the energy more rapidly. However, our original motivation for deriving an alternative formulation of the ASB algorithm was to be able to include deconvolution. In this case, the Euler-Lagrange equation of the \(M\)-subproblem in the strategy of Goldstein et al. (2010) would involve inverting the operator \(\nabla ^{T}\nabla + \mathrm{K}^{T}\!\mathrm{K}\). We expect that using a Gauss-Seidel strategy in that case reduces the average energy decrease per iteration.
4.5 2D Barcode Segmentation
Image segmentation can provide a bridge between image processing and image analysis. Traditionally, corrupted images are first restored and then analyzed to extract features of interest. One such application is barcode decoding. Choksi et al. (2011) applied a variational image-restoration framework to denoise and deblur 2D barcodes. We show that this problem can be reformulated and solved as a joint task. The goal here is not to design an efficient model or algorithm for 2D barcode analysis, but to illustrate how a real-world problem can be formulated and solved within the present framework.
Figure 5a shows a quick response (QR) code image corrupted with Gaussian blur and additive Gaussian noise (\({\mathrm{SNR}}=16\)). Moreover, \(16\,\%\) of all pixels are randomly removed from the corrupted image (Fig. 5b). Otsu thresholding is used to generate the initial mask (Fig. 5c). We use three different image models solved using the present ASBS with \(\lambda =0.01, \,\gamma =0.1\), and \(\tau _\beta =15\). The first one is the deconvolving Chan-Vese model (Fig. 5d). The second uses the same data-fitting energy, but an anisotropic TV regularizerFootnote 14, as proposed by Choksi et al. (2011) (Fig. 5e). In Algorithm 1, we only need to modify the \(\varvec{w_2}\)-subproblem: Instead of a coupled soft shrinkage applied to \(\varvec{w_2}\), two soft shrinkages are separately applied to each componentFootnote 15 of \(\varvec{w_2}\). The third model follows closely Choksi et al. (2011), but explicitly includes the inpainting problem: An \(L^1\) data-fitting energy is used with \(w_d\) encoding the inpainting combined with an anisotroptic TV regularizer (Fig. 5f).
Segmentation of a noisy, blurred QR code with missing data. (a) QR code of the GLM wikipedia page URL. (b) Noisy (Gaussian noise, \({\mathrm{SNR}}=16\)), blurred (Gaussian blur, standard deviation 2 pixels) QR code with \(16\,\%\) randomly missing pixels. (c) Otsu thresholding of (b). (d–f) ASBS results for a two-region segmentation/deconvolution (\(\lambda =0.01, \,\gamma =0.1\), and \(\tau _\beta =15\)). (d–f) GLM model based on a Gaussian noise model, the true inpainting mask and the true blurring kernel coupled with an isotropic (d) or anisotropic (e) TV regularizer. (f) \(L^1\) data-fitting model with an anisotropic TV regularizer
Figure 5b and its Otsu-thresholded version, Fig. 5c, can not be decoded by a standard smartphone application, whereas all three reconstructions can (Fig. 5d–f). The main difference between the three reconstructions is the quality of square-like features. The first model uses an isotropic geometric prior, causing rounded corners. The other two models use an anisotropic geometric prior, favoring rectangles with edges aligned with the image axes. This results in sharper corners and edges. The third model is known to yield contrast-invariant energies and induce a geometric scale-space where small features can be recovered robustly (see e.g., Chan and Esedoḡlu 2005).
4.6 3D Segmentation of Confocal Microscopy Data
Confocal microscopy and recombinant protein technology enable biologists to address questions from subcellular dynamics in live cells to tissue formation. This requires accurately reconstructing and quantifying structures from noisy and blurred images. We illustrate the flexibility of our framework by performing 3D reconstructions of a complex-shaped subcellular structure—the endoplasmic reticulum (ER)—and of a multi-cellular structure—the Drosophila wing disc—from stacks of confocal images. For a biophysical application of ER reconstructions we refer to Sbalzarini et al. (2005, 2006). The Drosophila wing data come from Zartman et al. (2013).
Figure 6a,d show the maximum-intensity projections of the raw imagesFootnote 16 of the ER (\(325\times 250\times 16\) pixels) and the wing disc (\(512\times 512\times 12\) pixels), respectively. We use model (11) with a Poisson likelihood, \(\lambda =0.04\), a Gaussian model PSF with standard deviations estimated from the data. The present ASBS uses \(\tau _\beta =15, \,\gamma =0.05\), and is initialized with an Otsu-thresholded image. Fig. 6b,e shows the resulting segmentations. In both cases, the biological prior is that these structures are connected. We thus highlight the largest connected component in red.
Segmenting biological structures imaged with confocal microscopy. (a, d) Maximum-intensity projections of the inverted images of (a) an ER (Image: Helenius group, ETH Zürich) and (d) a Drosophila wing disc (Image: Basler group, University of Zürich). (b, e) ASBS two-region segmentation with a Poisson likelihood and an estimated Gaussian PSF, using the a posteriori upper-bound (21) (green). The largest connected component (LCC) is shown in red. (c, f) Comparison of the LCC from joint deconvolution/segmentation (red) and from the sequential approach (blue). (c) For the ER, the LCC from the joint approach (transparent red) is larger and contains the LCC from the sequential approach. (f) The LCC of the wing disc obtained by the sequential approach (blue) fills the space in \(z\) and misses the embedding of the tissue surface in 3D
Using these two examples, we compare our coupled denoising/deconvolution/segmentation with the classical way of first performing image restoration and then segmenting the restored image. Denoising and deconvolution in the sequential approach are done using a TV-regularized Richardson-Lucy (Dey et al. 2004) deconvolution algorithm, which is adapted to Poisson statistics. The restored images are then segmented using AM with a Chan-Vese model. The geometric inverse problem is solved using graph-cuts, since they provide good theoretical guarantees for two-region segmentation. A visual comparison of the sequential and joint approaches is shown in Fig. 6c, f. The joint approach yields visually better results than the sequential one. We quantify this using known ground-truth data. For both datasets, we generate ground-truth segmentations using a discrete restoration/segmentation algorithm with a piecewise smooth image model (Cardinale et al. 2012). From the resulting segmentation, we generate artificial data by blurring a piecewise-constant model with the estimated PSF and adding Poisson noise (ER: \({\mathrm{SNR}}\approx 4\), Wing: \({\mathrm{SNR}}\approx 5.2\)), see Fig. 7a, e. Our joint approach directly uses these images as input (\(\lambda = 0.04, \,\tau _\beta = 15, \,\gamma = 0.05\)). For the sequential approach, we tune the parameters such as to maximizeFootnote 17 the signal-to-error ratio SER, see Vonesch and Unser (2008) in each case.
Segmentation of synthetic wing discs. a–c Maximum-intensity projections of (a) the synthetic noisy, blurred image, (b) the reconstruction by joint deconvolution/segmentation (\(\lambda =0.04\)), and (c) the reconstruction from the sequential approach (\(\lambda =0.01\)). (d–i) show for the same central slice of the image stack: (d) ground truth, (e) synthetic noisy, blurred image, (f) deconvolved image using TV-regularized Richardson-Lucy deconvolution, (g) result from joint deconvolution/segmentation. Results from the sequential approach are shown in (h) \(\lambda =0.01\)) and (i) (\(\lambda =0.04\))
We quantitatively compare the two approaches using the MCC (cf. Sect. 4.2) and the gain (in dB), defined as the SER difference between the estimated piecewise-constant image and ground truth. For both datasets, the joint approach outperforms the sequential one, both in MCC and in SER gain. For the artificial ER, the joint approach achieves an MCC of \(0.8018\) and a SER gain of \(1.9290\) dB, whereas the sequential approach achieves MCCs of \(0.6970\) (\(\lambda = 0.01\)) and \(0.6974\) (\(\lambda = 0.04\)), and SER gains of \(1.1778\) dB (\(\lambda = 0.01\)) and \(1.1799\) dB (\(\lambda = 0.04\)). For the artificial wing disc, the joint approach achieves an MCC of \(0.7763\) and a SER gain of \(4.1759\) dB. The sequential approach achieves MCCs of \(0.3852\) (\(\lambda = 0.01\)) and \(0.2188\) (\(\lambda = 0.04\)), and SER gains of \(1.6208\) dB and \(1.1369\) dB. Even though we do not see a big difference between the two approaches when projecting the reconstructed images (Fig. 7b,c), we observe that the restored image in Fig. 7f displays enhanced structures from adjacent \(z\)-slices. These spurious structures appear at low regularization, since in a sequential approach the segmentation is unaware of the restoration task (Fig. 7h). At higher regularization, these artifacts reduce at the expense of poorer segmentation accuracy (Fig. 7i). The difference in quality between the joint and the sequential approach is mainly caused by the deconvolution task, rather than the segmentation algorithm used. When jointly performing deconvolution and segmentation, the segmentation image model provides qualitatively different regularization for the deconvolution.
5 Discussion and Conclusion
We presented a framework in which image restoration and segmentation can be jointly formulated. We have shown how to encode many image restoration problems in the likelihood of a Bayesian image model. While we did not analyze this formulation in its full generality, we focused on a large family of forward models, extending the exponential family formulation of Lecellier et al. (2010) to regression using generalized linear models. This allowed incorporating image-restoration tasks via the prior data weights \(w_d\) and the design matrix \(\varvec{X}\). Another perspective is to see the joint formulation as a way to regularize ill-posed variational image-restoration problems by constraining the reconstructed image to be in a segmentation model class, here a piecewise-constant two-region model. This is illustrated numerically in our 3D real-world experiments in Sect. 4.6.
We have restricted ourselves to four members of the exponential family to explore the range of scaling in the mean of the variance function, from constant (Gaussian) to quadratic (Bernoulli and gamma). Other members of this family are adapted to the noise model relevant to the data at hand (see Lecellier et al. 2010, for other applications). However, the EF restricts the range of denoising tasks amenable to this formulation. Nevertheless, it allows linking to a general class of information measures, the Bregman divergences. One can thus view the joint segmentation/restoration problem in a dual way made precise in this article, either as a spatially regularized regression problem (the GLM perspective) or as a spatially regularized clustering problem based on a Bregman divergence (the information-theoretic perspective). This extends the work of Banerjee et al. (2005) and constitutes a first contribution toward a systematic classification of the likelihoods in Bayesian image models. The presented formulation includes existing image-segmentation models and formulates several new ones. Some existing models, however, do not fit our formulation. An example is the \(L^1\) data-fitting energy of Chan and Esedoḡlu (2005) corresponding to a Laplace distribution, which is not a member of the exponential family. Hence, extending the classification of likelihoods seems important.
The presented GLM formulation suggests new models not present in literature. Most notably, via the link function \(g\) the GLM framework allows for a non-linear relationship between the linear predictor \(\eta \) and the expectation \(\mu \) of the noise model. As far as we know, this has so far not been used in image processing. It is also possible to further extend the range of restoration tasks amenable to the presented formulation. For example, we only considered kernels \(\mathrm{K}\) representing convolutions. One could, however, also consider down-sampling and zooming/super-resolution operations \(\mathrm{K}\) see, e.g., Marquina and Osher (2008).
The full image model uses an isotropic total variation prior with weights \({w_b}\). The regularization term was not the main focus here, we did not study the possibility of different geometric priors. Nevertheless, as shown in the QR barcode example, an anisotropic TV prior can be used with little modification to the framework. The convex relaxation results remain valid as long as the prior satisfies a co-area-like formula. Considering other geometric priors could be particularly beneficial for adapting the geometric prior to the problem at hand, or for coupling image segmentation other image restoration tasks. For example, we have only considered the TV-inpainting model, whereas most of the work on inpainting focuses on designing specialized priors for this task (Chan and Shen 2005; Aubert and Kornprobst 2006). For the sake of simplicity we have restricted our discussion to single scalar images for which a two-region segmentation problem with piecewise-constant photometry is solved. An extension to vector-valued images can be achieved using vector GLMs (see e.g., Song 2007).
Some of the inverse-problem results presented here are specific to the GLM class of forward models. These are the photometric estimation using Fisher scoring and the derivation of the shape gradient, extending the results of Lecellier et al. (2010) from the REF to the GLM class. Generalizing these results to more than two regions is straightforward. We showed that a general coupling (i.e., a general \(\mathrm{K}\)) of image segmentation and restoration prohibits exact convex relaxation by thresholding, even for a two-region problem. This is in contrast to the literature on linear data-fitting energies, where a lack of exact convex relaxation comes from the fact that the co-area formula for the TV regularizer does not generalize to more than two regions. Techniques developed to convexify multi-region problems, such as functional lifting (see Pock et al. 2008), could potentially also be used in our framework in order to obtain convex formulations of the forward problem for general \(\mathrm{K}\) and for non-convex likelihood energies, such as gamma noise. The photometric/geometric inverse problem is in general not jointly convex, due to the bilinear form of the linear predictor \(\eta \). Extending the results of Brown et al. (2012) to our framework, however, would allow a completely convex formulation of the joint inverse problem.
Another contribution made here was the introduction of a new splitting scheme for the alternating split-Bregman algorithm as applied to image segmentation. This contribution is also valid for data-fitting energies not in the GLM class and for more general regularizers. This is shown in Sect. 4.5 where a Laplace data-fitting energy and an anisotropic TV regularizer are used. We have extended our ASB to multiple regions in Paul et al. (2011). We chose the ASB algorithm as a prototypical convex solver adapted to inverse problems in image processing. However, many aspects of the present framework can also be used with other optimization algorithms, such as those by Chambolle and Pock (2011), Lellmann and Schnörr (2011) and Chambolle et al. (2012).
Notes
For \(d\)-dimensional exponential families of distributions, regularity requires additional conditions that are automatically satisfied for \(d=1\); c.f. Banerjee et al. (2005).
The link function is part of the forward model and could serve different purposes. A first one could be to linearize seemingly nonlinear regression problems in the spirit of an implicit Box-Cox transform without actually transforming the data; \(g\) only acts on the mean of the p.d.f. A second use could be to design \(g\) such as to map \(\varvec{\beta }\) into the natural range of the mean parameter, hence avoiding range constraints during parameter estimation.
Table 1 Image restoration in the GLM/Bregman framework ANalysis Of VAriance
Other possible uses of \(w_d\) have been presented by Leung and Osher (2005).
Convolution \(*\) operating on a vector or a matrix is meant component-wise.
Generalized Bregman divergences relax this assumption to subdifferentiable \(\psi \). However, we restrict ourselves to continuously differentiable \(\psi \) in order to be able to use the duality theorem with the REF (Banerjee et al. 2005).
\(b^\star (\mu ) \,{:=}\, \sup _{\theta \in \mathrm dom (b)} (\theta \mu -b(\theta ))\), where \(\mathrm dom (b)\) is the effective domain of \(b\). For a precise statement of the duality in the REF, see the online appendix.
Rigorously, we need that \(\int _{\varOmega _I}\left|\ell (u_0~| {{\varvec{x}}},{{\widetilde{\theta }}_\mathrm{MLE}})\right|\mathrm{d}{{\varvec{x}}}< \infty \).
Examples of such conditions are: \(\ell ({{\varvec{x}}},\varvec{\beta })\) is \({\varOmega _I}\)-almost everywhere \(\varvec{\beta }\)-differentiable and \(\left|\varvec{s}({{\varvec{x}}},\varvec{\beta })\right|\) is \({\varOmega _I}\)-almost everywhere bounded by an integrable function of x only.
i.e., belongs to \(L^1({\varOmega _I})\).
Here, \(w_1^{k+1} = \frac{\gamma w_d \Delta \beta (u_0-\beta _1)+b_1^k+\mathrm{K}\left[ M^{k+1}\right] }{1+\gamma (\Delta \beta )^2w_d}\) pointwise.
Goudail et al. (2004) use a Gaussian SNR, which is the square of ours. Hence, our definition differs from theirs by a square root.
Defined in 2D as \(\int _{\varOmega _I}\left|\partial _1 M({{\varvec{x}}})\right|+\left|\partial _2 M({{\varvec{x}}})\right|\mathrm{d}{{\varvec{x}}}\).
The derivation is straightforward and not shown here.
We show inverted images for visual clarity.
This may seem overly conservative, but avoids obvious failures of the sequential approach due to unstable deconvolution.
References
Alliney, S. (1997). A property of the minimum vectors of a regularizing functional defined by means of the absolute norm. Signal Processing IEEE Transactions on, 45(4), 913–917.
Art, J. (2006). Photon detectors for confocal microscopy. In J. B. Pawley (Ed.), Handbook of biological confocal microscopy (pp. 251–264). Berlin: Springer.
Aubert, G., & Aujol, J. F. (2008). A variational approach to removing multiplicative noise. SIAM Journal on Applied Mathematics, 68(4), 925–946.
Aubert, G., & Kornprobst, P. (2006). Mathematical problems in image processing: Partial differential equations and the calculus of variations, applied mathematical sciences, vol 147, 2nd edn. Berlin: Springer.
Aubert, G., Barlaud, M., Faugeras, O., & Jehan-Besson, S. (2003). Image segmentation using active contours: Calculus of variations or shape gradients? SIAM Journal of Applied Mathematics, 63(6), 2128–2154.
Aujol, J. F., Gilboa, G., Chan, T., & Osher, S. (2006). Structure-texture image decomposition modeling, algorithms, and parameter selection. International Journal of Computer Vision, 67, 111–136.
Baldi, P., Brunak, S., Chauvin, Y., Andersen, C. A. F., & Nielsen, H. (2000). Assessing the accuracy of prediction algorithms for classification: An overview. Bioinformatics, 16(5), 412–424.
Banerjee, A., Merugu, S., Dhillon, I., & Ghosh, J. (2005). Clustering with Bregman divergences. The Journal of Machine Learning Research, 6, 1705–1749.
Barndorff-Nielsen, O. E. (1978). Information and exponential families in statistical theory (Wiley series in probability and mathematical statistics). Chichester: Wiley.
Bertero, M., & Boccacci, P. (1998). Introduction to inverse problems in imaging. London: Taylor and Francis.
Bertero, M., Poggio, T., & Torre, V. (1988). Ill-posed problems in early vision. Proceedings of the IEEE, 76(8), 869–889.
Bovik, A. C. (2005). Handbook of image and video processing (communications, networking and multimedia) (2nd ed.). Orlando: Academic Press, Inc.
Boykov, Y., Veksler, O., & Zabih, R. (2001). Fast approximate energy minimization via graph cuts. Pattern Analysis and Machine Intelligence, IEEE Transactions, 23(11), 1222–1239.
Bresson, X., Esedo\({\bar{\text{ g}}}\)lu, S., Vandergheynst, P., Thiran, J. P., & Osher, S. (2007). Fast global minimization of the active contour/snake model. Journal of Mathematical Imaging and Vision, 28, 151–167.
Brown, E., Chan, T., Bresson, X. (2012). Completely convex formulation of the Chan-Vese image segmentation model. International Journal of Computer Vision, 98(1), 103–121.
Brox, T., Rousson, M., Deriche, R., & Weickert, J. (2010). Colour, texture, and motion in level-set based segmentation and tracking. Image and Vision Computing, 28(3), 376–390.
Burger, M., & Hintermüller, M. (2005). Projected gradient flows for BV/level-set relaxation. PAMM, 5(1), 11–14.
Burger, M., & Osher, S. (2005). A survey on level set methods for inverse problems and optimal design. European Journal of Applied Mathematics, 16(02), 263–301.
Cardinale, J., Paul, G., & Sbalzarini, I. (2012). Discrete region competition for unknown numbers of connected regions. Image Processing IEEE Transactions, 21(8), 3531–3545.
Caselles, V., Catté, F., Coll, T., & Dibos, F. (1993). A geometric model for active contours in image processing. Numerische Mathematik, 66, 1–31.
Caselles, V., Kimmel, R., & Sapiro, G. (1997). Geodesic active contours. International Journal of Computer Vision, 22, 61–79.
Chambolle, A. (2004). An algorithm for total variation minimization and applications. Journal of Mathematical Imaging and Vision, 20, 89–97.
Chambolle, A., & Pock, T. (2011). A first-order primal-dual algorithm for convex problems with applications to imaging. Journal of Mathematical Imaging and Vision, 40, 120–145.
Chambolle, A., Cremers, D., & Pock, T. (2012). A convex approach to minimal partitions. SIAM Journal on Imaging Sciences, 5(4), 1113–1158.
Chan, T. F., & Esedo\({\bar{\text{ g}}}\)lu, S. (2005). Aspects of total variation regularized \(L^1\) function approximation. SIAM Journal on Applied Mathematics, 65(5), 1817–1837.
Chan, T. F., & Shen, J. J. (2005). Image processing and analysis: Variational, PDE, wavelet, and stochastic methods. Philadephia: Society for Industrial and Applied Mathematics.
Chan, T. F., & Vese, L. (2001). Active contours without edges. Image Processing IEEE Transactions, 10(2), 266–277.
Chan, T. F., Esedo\({\bar{\text{ g}}}\)lu, S., & Nikolova, M. (2006). Algorithms for finding global minimizers of image segmentation and denoising models. SIAM Journal on Applied Mathematics, 66(5), 1632–1648.
Chesnaud, C., Réfrégier, P., & Boulet, V. (1999). Statistical region snake-based segmentation adapted to different physical noise models. Pattern Analysis and Machine Intelligence IEEE Transactions, 21(11), 1145–1157.
Choksi, R., van Gennip, Y., & Oberman, A. (2011). Anisotropic total variation regularized \(L^1\) approximation and denoising/deblurring of 2D bar codes. Inverse Problems and Imaging, 5(3), 591–617.
Cremers, D., Rousson, M., & Deriche, R. (2007). A review of statistical approaches to level set segmentation: Integrating color, texture, motion and shape. International Journal of Computer Vision, 72, 195–215.
Delfour, M., & Zolésio, J. (2011). Shapes and geometries: Metrics, analysis, differential calculus, and optimization, (Vol. 22). Philadelphia: Society for Industrial Mathematics.
Dey, N., Blanc-Féraud, L., Zimmer, C., Kam, Z., Olivo-Marin, J.C., Zerubia, J. (2004). A deconvolution method for confocal microscopy with total variation regularization. In: Biomedical imaging: Nano to macro, 2004. IEEE International Symposium on, (Vol. 2) (pp 1223–1226) . Arlington.
Esser, E. (2009). Applications of Lagrangian-based alternating direction methods and connections to split Bregman. Technical report UCLA Computational and Applied Mathematics.
Geiger, D., & Yuille, A. (1991). A common framework for image segmentation. International Journal of Computational Vision, 6, 227–243.
Geman, S., & Geman, D. (1984). Stochastic relaxation, Gibbs distributions, and the Bayesian restoration of images. Pattern Analysis and Machine Intelligence IEEE Transactions, 6(6), 721–741.
Goldstein, T., & Osher, S. (2009). The split Bregman method for \(l^1\)-regularized problems. SIAM Journal on Imaging Sciences, 2(2), 323–343.
Goldstein, T., Bresson, X., & Osher, S. (2010). Geometric applications of the split Bregman method: Segmentation and surface reconstruction. Journal of Scientific Computing, 45, 272–293.
Goudail, F., Réfrégier, P., Ruch, O. (2003). Definition of a signal- to-noise ratio for object segmentation using polygonal MDL-based statistical snakes. In: Energy minimization methods in computer vision and pattern recognition, Vol. 2683 (pp. 373–388). Berlin: Springer.
Goudail, F., Réfrégier, P., & Delyon, G. (2004). Bhattacharyya distance as a contrast parameter for statistical processing of noisy optical images. Journal of the Optical Society of America A, 21(7), 1231–1240.
Greig, D. M., Porteous, B. T., & Seheult, A. H. (1989). Exact maximum a posteriori estimation for binary images. Journal of the Royal Statistical Society Series B (Methodological), 51(2), 271–279.
Hansen, P. C., Nagy, J. G., & O’Leary, D. P. (2006). Deblurring images: Matrices, spectra, and filtering (fundamentals of algorithms 3) (fundamentals of algorithms). Philadelphia: Society for Industrial and Applied Mathematics.
Hebert, T., & Leahy, R. (1989). A generalized EM algorithm for 3D Bayesian reconstruction from Poisson data using Gibbs priors. Medical Imaging IEEE Transactions, 8(2), 194–202.
Helmuth, J., Sbalzarini, I. (2009). Deconvolving active contours for fluorescence microscopy images. In: Advances in visual xomputing, lecture notes in computer science (Vol. 5875, pp. 544–553). Berlin: Springer.
Helmuth, J., Burckhardt, C., Greber, U., & Sbalzarini, I. (2009). Shape reconstruction of subcellular structures from live cell fluorescence microscopy images. Journal of Structural Biology, 167(1), 1–10.
Jung, M., Chung, G., Sundaramoorthi, G., Vese, L., Yuille, A. (2009). Sobolev gradients and joint variational image segmentation, denoising and deblurring. In: SPIE Electronic Imaging Conference Proceedings, Computational Imaging VII, SPIE (Vol. 7246).
Kass, M., Witkin, A., & Terzopoulos, D. (1988). Snakes: Active contour models. International Journal of Computer Vision, 1, 321–331.
Kersten, D., Mamassian, P., & Yuille, A. (2004). Object perception as bayesian inference. Annual Review of Psychology, 55, 271–304.
Lecellier, F., Jehan-Besson, S., Fadili, J., Aubert, G., Revenu, M. (2006). Statistical region-based active contours with exponential family observations. In: Proceedings of IEEE International Acoustics, Speech and Signal Processing Conference ICASSP 2006 (Vol. 2).
Lecellier, F., Fadili, J., Jehan-Besson, S., Aubert, G., Revenu, M., & Saloux, E. (2010). Region-based active contours with exponential family observations. Journal of Mathematical Imaging and Vision, 36, 28–45.
Lellmann, J., & Schnörr, C. (2011). Continuous multiclass labeling approaches and algorithms. SIAM Journal on Imaging Sciences, 4(4), 1049–1096.
Leung, S., Osher, S. (2005). Global minimization of the active contour model with TV-inpainting and two-phase denoising. In: Variational, geometric, and level set methods in computer vision (Vol. 3752, pp. 149–160). Springer: Berlin.
Malladi, R., Sethian, J., & Vemuri, B. (1995). Shape modeling with front propagation: A level-set approach. Pattern Analysis and Machine Intelligence IEEE Transactions, 17(2), 158–175.
Marquina, A., & Osher, S. (2008). Image super-resolution by TV-regularization and Bregman iteration. Journal of Scientific Computing, 37, 367–382.
Martin, P., Réfrégier, P., Goudail, F., & Guérault, F. (2004). Influence of the noise model on level-set active contour segmentation. Pattern Analysis and Machine Intelligence IEEE Transactions, 26(6), 799–803.
Matthews, B. (1975). Comparison of the predicted and observed secondary structure of t4 phage lysozyme. Biochimica et Biophysica Acta (BBA)—Protein Structure, 405(2), 442–451.
McCullagh, P., & Nelder, J. (1989). Generalized linear models, 2nd edn. London: Chapman and Hall/CRC.
Mumford, D. (1994). The Bayesian rationale for energy functionals. In: Geometry-driven diffusion in computer vision (pp. 141–153). Dordrecht: Kluwer Academic Publishers.
Mumford, D., & Shah, J. (1989). Optimal approximations by piecewise smooth functions and associated variational problems. Communications on Pure and Applied Mathematics, 42(5), 577–685.
Nelder, J., & Wedderburn, R. (1972). Generalized linear models. Journal of the Royal Statistical Society Series A (General), 135(3), 370–384.
Nikolova, M. (2004). A variational approach to remove outliers and impulse noise. Journal of Mathematical Imaging and Vision, 20, 99–120.
Osher, S., & Fedkiw, R. (2003). Level set methods and dynamic implicit surfaces, applied mathematical sciences (Vol. 153). New York: Springer.
Osher, S., & Paragios, N. (2003). Geometric level set methods in imaging, vision, and graphics. New York: Springer.
Paragios, N., & Deriche, R. (2002). Geodesic active regions: A new framework to deal with frame partition problems in computer vision. Journal of Visual Communication and Image Representation, 13(1–2), 249–268.
Paul, G., Cardinale, J., Sbalzarini, I. (2011). An alternating split Bregman algorithm for multi-region segmentation. In: Signals, systems and computers (ASILOMAR), 2011 Conference Record of the Forty Fifth Asilomar Conference on, (pp. 426–430).
Pock, T., Schoenemann, T., Graber, G., Bischof, H., Cremers, D. (2008). A convex formulation of continuous multi-label problems. In: Computer vision-ECCV 2008 (Vol. 5304, pp 792–805). Berlin: Springer.
Pock, T., Chambolle, A., Cremers, D., Bischof, H. (2009). A convex relaxation approach for computing minimal partitions. In: IEEE Conference on Computer vision and pattern recognition, 2009. CVPR 2009 (pp. 810–817).
Rudin, L. I., Osher, S., & Fatemi, E. (1992). Nonlinear total variation based noise removal algorithms. Physica D: Nonlinear Phenomena, 60(1–4), 259–268.
Sbalzarini, I. F., Mezzacasa, A., Helenius, A., & Koumoutsakos, P. (2005). Effects of organelle shape on fluorescence recovery after photobleaching. Biophysical Journal, 89(3), 1482–1492.
Sbalzarini, I. F., Hayer, A., Helenius, A., & Koumoutsakos, P. (2006). Simulations of (an)isotropic diffusion on curved biological surfaces. Biophysical Journal, 90(3), 878–885.
Sethian, J. (1999). Level set methods and fast marching methods: Evolving interfaces in computational geometry, fluid mechanics, computer vision, and material science. Cambridge: Cambridge University Press.
Setzer, S. (2011). Operator splittings, Bregman methods and frame shrinkage in image processing. International Journal of Computer Vision, 92, 265–280.
Setzer, S., Steidl, G., & Teuber, T. (2010). Deblurring Poissonian images by split Bregman techniques. Journal of Visual Communication and Image Representation, 21(3), 193–199.
Shepp, L. A., & Vardi, Y. (1982). Maximum likelihood reconstruction for emission tomography. Medical Imaging IEEE Transactions, 1(2), 113–122.
Song, P.X.K. (2007). Vector generalized linear models. In: Correlated data analysis: Modeling, analytics, and applications, Springer series in statistics (pp. 121–155). New York: Springer.
Strang, G. (1999). The discrete cosine transform. SIAM Review, 41(1), 135–147.
Tai, X.C., Wu, C. (2009). Augmented lagrangian method, dual methods and split bregman iteration for rof model. In: Scale space and variational methods in computer vision (Vol. 5567, pp. 502–513). Berlin: Springer.
Vogel, C. R. (2002). Computational methods for inverse problems. Philadelphia: Society for Industrial and Applied Mathematics.
Vonesch, C., & Unser, M. (2008). A fast thresholded Landweber algorithm for wavelet-regularized multidimensional deconvolution. IEEE Transactions on Image Processing, 17(4), 539–549.
Zartman, J., Restrepo, S., Basler, K. (2013). A high-throughput template for optimizing Drosophila organ culture with response-surface methods. Development, 143(3), 667–674.
Zhu, S., & Yuille, A. (1996). Region competition: Unifying snakes, region growing, and Bayes/MDL for multiband image segmentation. IEEE Transactions on Pattern Analysis and Machine Intelligence, 18(9), 884–900.
Acknowledgments
We thank Jo A. Helmuth for sharing his experience in many discussions. JC and GP were funded through CTI grant 9325.2-PFLS-LS from the Swiss Federal Commission for Technology and Innovation (to IFS in collaboration with Bitplane, Inc). This project was further supported with grants from the Swiss SystemsX.ch initiative, grants LipidX and WingX, to IFS. We thank J. Zartman, S. Restrepo, and K. Basler for providing the Drosophila wing disc example image.
Author information
Authors and Affiliations
Corresponding author
Electronic supplementary material
Below is the link to the electronic supplementary material.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution License which permits any use, distribution, and reproduction in any medium, provided the original author(s) and the source are credited.
About this article
Cite this article
Paul, G., Cardinale, J. & Sbalzarini, I.F. Coupling Image Restoration and Segmentation: A Generalized Linear Model/Bregman Perspective. Int J Comput Vis 104, 69–93 (2013). https://doi.org/10.1007/s11263-013-0615-2
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11263-013-0615-2