Introduction

The rate of outcrossing and the magnitude of inbreeding depression are key parameters determining the evolution of plant and animal mating systems (Charlesworth and Charlesworth, 1987; Goodwillie et al., 2005; Jarne and Auld, 2006; Escobar et al., 2009). Outcrossing rates also affect the amount and partitioning of genetic diversity in natural populations (Hamrick and Godt, 1996; Charlesworth, 2003; Glémin et al., 2006) and the amount of inbreeding depression (Husband and Schemske, 1996). Furthermore, in a world with increasing anthropogenic disturbance, measures of outcrossing rates and inbreeding depression are important in conservation efforts (Aguilar et al., 2006; Eckert et al., 2010).

Inbreeding depression can be measured directly using experimental crosses in laboratory/greenhouse populations, or indirectly using genetic markers in natural populations. Ritland (1990) suggested a method for the latter approach simultaneously estimating inbreeding depression (ID) and the outcrossing rate (t) of natural populations from genetic marker data. ID reduces the homozygosity of adults, measured by the mean inbreeding coefficient (F), relative to zygotes. F changes because inbred individuals are less likely to survive to adulthood and successfully produce offspring. ID is estimated from the magnitude of the change in F from zygote to adult with the zygote F inferred from the outcrossing rate. In plants, t and F are typically estimated from progeny arrays (Jarne and David, 2008). Seed families are collected from natural populations, grown in a greenhouse, and individuals from each seed family are genotyped at variable marker loci. The MLTR software, which implements a multilocus estimation model (Ritland and Jain, 1981; Ritland, 2002), is then usually used for statistical analysis of genotypic data (Goodwillie et al., 2005).

The direct and indirect methods to estimate ID each have their respective advantages and disadvantages. One benefit of using experimental crosses over field-based methods is that population substructure (for example, biparental inbreeding or the Wahlund effect) may be less of a concern (Jarne and David, 2008). Experimental crosses are also often less expensive and avoid the technical problems associated with marker selection and genotyping. However, many organisms are not experimentally tractable in the laboratory or greenhouse. Furthermore, several studies have shown that inbreeding depression can be more severe under natural, stressful conditions (Dudash, 1990; Crnokrak and Roff, 1999; Cheptou et al., 2000; Keller et al., 2002; Armbruster and Reed, 2005; Hayes et al., 2005). Perhaps the greatest advantage of genetic marker-based methods is that inbreeding depression is estimated from survival and reproduction in nature.

Although a number of studies have used the Ritland approach to estimate ID (Dole and Ritland, 1993; Eckert and Barrett, 1994; Kohn and Biardi, 1995; Scofield and Schultz, 2006; Tamaki et al., 2009; Yang and Hodges, 2010), a frequent criticism of the method is that ID estimates are typically encumbered with high statistical uncertainty. Confidence bands on ID estimates routinely span the entire range of possible values. However, we suggest that this is not an intrinsic flaw of the method. Instead, the large uncertainty associated with marker-based ID estimates owes to the fact that experimental studies are not optimally designed for the joint estimation of t and F.

A typical plant mating system experiment involves a few hundred plants, 10–20 progeny genotyped from each of 10–20 field maternal plants. We suggest that a better design for estimating the joint distribution of t and F is one with more parents and fewer offspring per family. The advantage of this reallocation of effort is shown in the simulation results summarized by Table 1. Here, we repeatedly simulated genotypic data for three different mating systems (t=0.1, 0.5 or 0.9) and then sampled according to two experimental designs (see Materials and Methods for simulation details). Design 1 is similar to the standard (15 maternal families each with 15 offspring), while design 2 maximizes the number of families. We assume that the maternal plants are genotyped, so each design involves 240 genotyped plants.

Table 1 The s.d. of estimates for population outcrossing rate (t) and adult inbreeding coefficient (F) are given for six distinct scenarios
Full size table

Applying MLTR to each of 50 replicates of each scenario, we find that both designs yield approximately unbiased estimates for both t and adult F, that is, the means of estimates are equal to the true values. However, the variance among replicate simulations differs strikingly between experimental designs. For t, differences are small, with design 1 slightly more precise than design 2. For adult F however, the standard deviation among estimates, which is what the standard error in a single real analysis is intended to approximate, is 3–4 times greater for design 1 than design 2. Taken together, these results suggest that a modified sampling scheme can greatly improve estimation of adult F, and hence of ID.

The simulation of Table 1 differs from most real studies in that we assumed complete maternal genotypes. In practice, field-sampled maternal tissue is often unavailable or insufficient in quality to score maternal genotypes. In these circumstances, mating system estimation requires inference of the maternal genotype from progeny genotypes. This works most efficiently with larger progeny sets unless the species is highly selfing (Brown and Allard, 1970; Ritland, 1986). Therefore, the need to infer maternal genotypes is mainly why larger family sizes are used in practice.

We have found that if MLTR is applied to data with small family sizes and unknown maternal genotypes, estimation of t and adult F becomes problematic (Figure 1). The first set of Results presented in this paper documents estimation bias for both t and F when family sizes are small. In response to this observation, we develop a Bayesian method for the joint estimation of t and F implemented in the program BORICE (Bayesian Outcrossing Rate and Inbreeding Coefficient Estimation). This procedure can provide unbiased estimates of t and F with small family sizes and incomplete (or absent) maternal genotype information. We present the theory in the next section and then two analyses. The first analysis is of simulated data (as in Figure 1) to demonstrate the performance of the method under known conditions. The second analysis is for real data from a single natural population of yellow monkeyflower (Mimulus guttatus).

Figure 1
figure 1

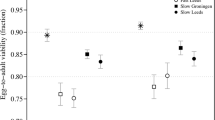
MLTR bias in the estimation of the population outcrossing rate (t) and adult inbreeding coefficient (F) using three experimental designs with small family sizes. Mean estimated t (a) and F (b) from simulations with 100 families each with four offspring (squares), 200 families each with two offspring (triangles), and 400 families each with one offspring (circles). Means are shown with standard errors. The solid black line represents no difference between the mean estimate and the true value.

Full size image

Materials and methods

Simulated genotype data

We simulate data for subsequent input to BORICE and/or MLTR from a mating system model with the following parameters: the number of marker loci, the number of alleles per marker, population allele frequencies, the number of maternal plants sampled, the number of offspring per family, and the population outcrossing rate. We assume marker loci are unlinked. In our initial set of simulations (Supplementary Tables S1 and S2 and Figures 1 and 2), we assume that the population outcrosses at a constant rate t (selfing occurs at rate 1–t) and that outcrossing is random. The first step in a simulation was to determine the inbreeding history (Ck=number of generations of selfing in the ancestry of individual k) for each maternal plant. The population consists of series of discrete ‘cohorts’ defined by individual inbreeding histories (Campbell, 1986; Kelly, 1999). Cohort 0 is outbred individuals (inbreeding coefficient F=0). Cohort 1 is selfed progeny of outbred individuals (F=1/2). Cohort 2 (F=3/4) is the selfed progeny of cohort 1 individuals, and so on. To simulate maternal genotypes, we assume the population distribution of inbreeding histories is geometric: Prob[Ck=X]=t(1−t)X. Ck values within a simulation run were sampled probabilistically from this distribution.

Figure 2
figure 2

Estimation of the population outcrossing rate (t) and adult inbreeding coefficient (F) in BORICE using three experimental designs with small family sizes. Mean t-max (a) and F-max (b) are reported from simulations of the same parameter combinations in Figure 1. The solid black line represents no difference between the mean estimate and the true value.

Full size image

The second step in a simulation is to sample maternal genotypes given Ck values and population allele frequencies. Probabilities of particular genotypes are given by the standard formulas (Hartl and Clark, 1989, p 250; Equation (2) below). Given the maternal genotype, we subsequently sampled progeny genotypes. By draw of a uniform random number, u, we first determined if the offspring was outcrossed (u<t) or selfed (u>t). If outcrossed, we sampled a gamete by randomly choosing one maternal allele at each locus. The complementary paternal allele was chosen probabilistically given population allele frequencies. For selfed progeny, two maternal gametes were formed and then paired. Progeny genotypes were the standard output, although maternal genotypes were also output if needed (as for Table 1).

We developed two elaborations of this program to test the robustness of BORICE. The first variant allowed the outcrossing rate to vary among maternal plants. Here, a uniform random value from 0 to 1 was sampled and assigned as the individual outcrossing rate to each maternal plant. The second variant allowed ‘correlated matings’. In this version, we did not sample pollen genotypes independently for each outcrossed progeny. Instead, the number of sires per maternal plant was specified as a model constant. We then sampled paternal genotypes according to the same rules as for maternal genotypes. Within a progeny set, we randomly sampled among sires for each outcrossed progeny and formed a gamete from this sire. If a single sire was specified per maternal plant, then the probability that outcrossed progeny were full sibs (the rp parameter of Ritland, 1989) was 1. With two sires per maternal plant, rp=0.5. The programs to execute these operations were written in C and are available upon request.

Tests of small family designs in MLTR

We used genotypic data simulated for three experimental designs and 15 true outcrossing rates to obtain t and F estimates from MLTR. The experimental designs were (a) 100 families each with four offspring, (b) 200 families each with two offspring, and (c) 400 families each with one offspring (400 individuals total in each design). Data were generated for 10 marker loci each with five equally frequent alleles. The maternal genotype was treated as unknown in all three designs and therefore was inferred in MLTR. Simulated data were run manually in MLTR for each replicate. Default settings were used except no bootstraps were performed. Maternal genotype inference was performed using the two options available in MLTR: (1) the ‘most likely parent’ method, and (2) choosing a parent at random in proportion to its prior probability (see the MLTR reference document for a description of these inference methods).

Bayesian estimation of t and F

We apply a Bayesian approach to estimate the population outcrossing rate and the distribution of individual inbreeding coefficients (F) among maternal individuals from progeny arrays. The unobserved inbreeding history cohort for each maternal plant (Ck) is a latent variable in our model. For cohort j, the individual inbreeding coefficient F=1–(1/2)j. This implies that the difference among cohorts vanishes as j gets larger and we bin all cohorts of 6 and greater. This cohort structure assumes that all outcrossing is random and all inbreeding results from recurrent self-fertilization, that is, there is no biparental inbreeding. If biparental inbreeding is substantial, individual inbreeding coefficients may vary more continuously. In MLTR, biparental inbreeding is suggested by a difference between individual and multi-locus estimates for t (Shaw et al., 1981; Ritland, 2002), although direct experimental approaches may prove more effective (Kelly and Willis, 2002; Herlihy and Eckert, 2004).

Unobserved maternal genotypes are also treated as latent variables. It is straightforward to calculate the likelihood for a set of progeny genotypes conditional on t, the maternal genotype, and population allele frequencies (Ritland and Jain, 1981; Wang, 2004). We assume that each offspring is independently determined as outcrossed or selfed, and for the former, siring of offspring within a family is independently determined. The likelihood for family k, lk, is:

Here, Mk is the vector of genotypes for maternal individual k, Aik is the vector of genotypes for offspring i of maternal individual k, and nk is the number of individuals in family k. Mk includes observed values as well as imputed (latent) values for any loci not directly genotyped from maternal DNA. Any missing values for the progeny vector (Aik) are ignored. Pr[Mk] is the probability of the maternal genotype, which depends on population allele frequencies and Ck, the inbreeding cohort of maternal individual k. Ck values for all maternal individuals are also treated as latent variables. is the probability of obtaining Aik given Mk by outcrossing, while is the corresponding probability if the offspring is produced by selfing. The likelihood for the entire dataset is the product of lk over families.

For a particular locus x, the maternal genotype probability is

where F is the inbreeding coefficient of the maternal plant and qxi is the population frequency of allele i at locus x. is a product over loci. are also products over loci given that we assume loci to be unlinked. is determined simply by Mendelian segregation, while also depends on the matrix of population allele frequencies.

We use Markov Chain Monte Carlo with the Metropolis-Hastings algorithm (Metropolis et al., 1953) to estimate the posterior distribution of each standard parameter (the allele frequencies and t) as well as each latent variable (all unknown maternal genotypes and the entire vector of maternal Ck). We assume a uniform prior density (0, 1) for t and a Dirichlet density (essentially a multivariate uniform density) for the prior on allele frequencies. An iteration of the chain has four stages: (1) propose and then accept/reject adjustment to t, (2) propose and then accept/reject adjustment to qxi with each locus (x) considered in series, (3) propose and then accept/reject new value for Ck with each maternal plant (k) considered in series, and (4) propose and then accept/reject a new genotype for a random locus of maternal genotype Mk within each family (k) considered in series.

The proposed value for the outcrossing rate t′ is equal to the current value (t) plus a small random increment, ɛ. ɛ is uniform on an interval (−σ, σ) around zero (our default value is σ=0.05). Reflection is employed to insure t′ is in the feasible range of 0 to 1. In other words, if t+ɛ=1.015, then t′=0.985. In general, the proposal ratio (R) is the product of the likelihood ratio, the prior ratio, and the Hastings ratio. The proposal scheme for t′, combined with a uniform prior on t, implies that both the prior ratio and Hastings ratio are 1. As a consequence, R for adjustments to t is simply:

If R>1, the step is taken (t′ is accepted). If R<1, then we draw a uniform random value (u) and accept t′ if u<R.

For allele frequencies, we track and update a score, yxi, corresponding to each allele (i) at each locus (x). These scores are bounded to non-negative values and the prior density is Gamma[1,1] for each allele. We assume independence of scores for the joint prior density. Allele frequencies are calculated as , with the summation taken over all alleles at locus x. We propose updates to yxi using the same method as updates to t, but here reflection occurs only at 0 (no upper bound). With this scheme, the qxi have a Dirichlet prior, the Hasting’s ratio is 1 and the prior ratio takes a simple form. The proposal ratio (R) for adjustments to yxi is

This updating scheme for allele frequencies follows work on proportion variables in phylogenetics (Lewis et al., 2010).

For the latent variables, we sample proposed values probabilistically given the current t and allele frequencies. The proposed value for inbreeding cohort of maternal plant k, Ck′, is sampled from a geometric distribution: . Imputed maternal genotypes are sampled from the probability distribution implied by current allele frequencies and Ck (see Equation (2)). With this scheme, proposed values for latent variables can match current values. While this may not be optimal for mixing, it is simple (prior ratio=Hasting’s ratio=1) and we have found that it performs well in practice. Observed acceptance rates are usually in the range of 40–75% for proposed updates to the latent variables when using default program settings. As changes to Ck and maternal genotypes affect the likelihood for only one family, family specific likelihoods are sufficient for the proposal ratio. For Ck′,

The description above is fully valid if null alleles are specified to be absent at all loci. If null alleles are allowed at a locus, the probability statements for maternal and offspring genotypes are modified to include the population frequency of null alleles as a parameter. We also allow an imputed maternal genotype even when the maternal genotype is observed. An observed maternal homozygote for allele i, AiAi, is consistent with that as the true genotype but the true genotype could also be A0Ai, a heterozygote of the observed allele with a null allele. With null alleles, progeny likelihoods are also modified. If the imputed maternal genotype is A0A0, the probability of progeny genotype AiAi is qxi/(1−qx0) by outcrossing or zero if by selfing. The (1−qx0) denominator of the outcrossing probability owes to the fact that we must condition on the observation of an offspring genotype (thus excluding the possibility that outcross pollen was null at locus x). If the imputed maternal genotype is A0Ai, the outcross probability for progeny genotype AjAj is 0.5 × qxj /(1−qx0) and for progeny genotype AiAi is 0.5 × qxi/(1−qx0)+0.5 × (qxi+qx0). For selfed progeny, the only possible observed progeny genotype is AiAi if the imputed maternal genotype is A0Ai. If both maternal alleles are non-null, then the probability of producing outcrossed but homozygous offspring is elevated by the additional possibility that pollen alleles are null. Selfed progeny genotype likelihood equations are unchanged if both maternal alleles are non-null. When null alleles are specified as present, allele frequencies are updated using the same scheme specified above.

Our method of dealing with nulls treats absent progeny genotypes as missing data. However, some information is lost with this method given that null alleles increase the likelihood of missing data. A family with an abundance of missing progeny genotypes may be an indicator that the maternal plant is likely to have one or two null alleles at a locus. The difficulty is that a diversity of reasons other than null alleles can yield missing data, for example, sample-specific PCR failure. A possible alternative to our approach is to explicitly model the multiple sources of error and include absent progeny genotypes in the likelihood calculations (Wang, 2004).

We have implemented the algorithms outlined above using two programming languages. A numerically efficient version was written in C. This version was applied to simulated genotypic data to evaluate performance (see Results). The experimental designs were identical to those used to test MLTR: 100 families each with four offspring, 200 families each with two offspring, and 400 families each with one offspring (400 individuals total in each design). Data were generated for ten marker loci each with five equally frequent alleles. The maternal genotype is unknown in all three designs and therefore must be inferred in BORICE.

The publicly available version of BORICE is open source and written in Python 2.7 (http://www.python.org/). BORICE functions through a graphical user interface written in PyQt 4.8.5, and can be run on Windows or Mac OS X machines. Genotype data for a population are imported into BORICE as a comma-separated text file. The program runs an initial check for impossible genotypes in the data set. Following the run, BORICE outputs text files with (1) the posterior distributions of the population inbreeding history, t, F, allele frequencies, maternal individual inbreeding histories, and maternal individual genotypes, (2) the mean values of the posterior distributions for t and F and the modal values t-max and F-max, (3) the credibility intervals (2.5 and 97.5 percentiles) for t and F, which are the Bayesian analog of 95% confidence intervals, and (4) the list of t, F and ln likelihood values from every 10 steps in the chain following the burn-in. Given that the posterior distributions for t, F and allele frequencies are continuous, the output consists of binned values ranging from 0 to 1 in increments of 0.01. t-max and F-max are the modal values for each posterior distribution.

Empirical application

Mimulus guttatus (Phrymaceae), the yellow monkeyflower, is a hermaphroditic and self-compatible plant species native to a diversity of habitats in the western United States. It occurs in both annual and perennial growth forms. We collected seed families of M. guttatus from a putatively perennial coastal population, Short Sands (SS; N 45 °45′35.2′, W 123 °57′52.3′), located in Tillamook Co., Oregon, USA. Mature fruits were collected randomly from individuals throughout the population in July, 2009. Seed families were then sown onto damp potting soil in the University of Kansas greenhouse in October 2009 and grown under standard conditions (see Arathi and Kelly, 2004) until young leaf tissue could be collected for DNA extraction. DNA was then extracted from 48 families with four offspring in each family using the CTAB method (see Marriage et al. (2009) for a detailed description of the protocol).

Multilocus genotypes were then determined for each individual using three microsatellite loci (AAT240, AAT367 and AAT374) identified as polymorphic in M. guttatus (Kelly and Willis, 1998). GenBank accession numbers and links to the GenBank entries for these loci are available at http://www.mimulusevolution.org/. PCR was used to amplify length polymorphisms at these loci. Each PCR mixture was 10 μl in total volume, and consisted of 2–10 ng of template DNA, 5 μM HEX- or FAM-labeled forward primers, 5 μM reverse primers, 250 μM of each dNTP, 25 mM MgCl2, 0.15 U Taq DNA polymerase (Promega, Madison, WI, USA) and 5 × PCR buffer (Promega). A touch-down PCR protocol for thermal cycling was implemented using an iCycler Thermal Cycler (BioRad, Hercules, CA, USA): 94 °C for 3 min, 10 cycles of denaturing at 94 °C for 30 s, annealing for 30 s and extension at 72 °C for 45 s; the initial annealing temperature was 62 °C decreased by 1 °C with each cycle, followed by 30 cycles of denaturing at 94 °C for 30 s, annealing using 52 °C for 30 s, and extension at 72 °C for 45 s, and a final extension at 72 °C for 20 min Capillary electrophoresis on an ABI 3130 Genetic Analyzer (Applied Biosystems, Foster City, CA, USA) was used to size PCR-amplified fragments. We sized fragments using GENEMAPPER 4.0 software (Applied Biosystems) calibrated with the ROX500 size standard (Applied Biosystems).

We applied both MLTR and BORICE to the data. Estimates in MLTR were obtained using the ‘most likely parent’ default setting and 1000 bootstraps (resampling families). For BORICE, we used a chain of 100 000 steps with a burn-in of the first 10 000 steps. This chain length was established sufficient because it yielded stable posterior estimates of t and F in replicate applications. Given the maximum posterior estimates for t and F, we calculated Ritland’s (1990) moment estimator for the relative fitness (ω) of selfed progeny in the SS population. Assuming F remains constant across generations, ω=2 × t × F/[(1–t)(1–F)]. The inbreeding depression (∂) is 1−ω.

Results

Tests of MLTR

When the maternal genotype was inferred, we found substantial estimation bias in MLTR estimates for both t and F for family sizes less than or equal to four (Supplementary Table S1). The outcrossing rate, t, was consistently overestimated with MLTR yielding estimates often 2–4 times greater than the true value for each of the three experimental designs (Figure 1a). Exceptions were those data for 400 families each with one offspring where true t was 0.5 or greater; in those scenarios, the MLTR estimate of t was zero. Adult F was upwardly biased in these designs (Figure 1b), most severely for true F⩽0.7. The exception was with 400 families (one offspring per family) and a true F<0.4. These results used the ‘most likely parent’ method to infer the maternal genotype. When instead the maternal genotype was inferred by choosing a parent at random in proportion to its prior probability, MLTR returned zero for all estimates of t and F (Supplementary Table S1). As expected, bias was minimal with families of eight or more offspring (results not shown).

Tests of BORICE

The Bayesian method implemented in BORICE yields unbiased estimates for t and adult F when applied to the same simulated data sets (compare Supplementary Table S2 with Table S1). At each of 15 t values tested, the average modal posterior t and F values differed minimally from the true t and F (Figure 2). The posterior distribution means for t and F differed only slightly from the modal values. Supplementary Table S2 summarizes results where null alleles were absent from simulated data and BORICE was set to run without nulls. To evaluate the consequences of null alleles for estimation, we generated simulated data with and without nulls and then applied both variants of the model. Supplementary Table S3 illustrates the effect of allowing null alleles in model fitting when none are present in the data. For this parameter set, allowing nulls did not bias estimates for t or F. However, the average ln likelihood is substantially lower than for the correct model where nulls are excluded (Supplementary Table S2). Supplementary Table S4 summarizes model fits when null alleles are present in the data and BORICE is specified to allow nulls. Posterior distributions for allele frequencies correctly identify nulls, although there is slight bias in estimates for a few parameter sets. We cannot compare the average ln likelihood values of correct (nulls allowed) and incorrect (nulls excluded) models because the latter model would routinely yield zero likelihood values.

We also tested if (1) varying the outcrossing rate of maternal plants or (2) correlated mating would bias the results of BORICE. Varying the outcrossing rate of maternal plants had minimal effect. Simulations with a constant outcrossing rate (t=0.5) for all maternal plants (mean t-max=0.502, s.e.=0.002; mean F-max=0.334, s.e.=0.003) are very similar to results with variable outcrossing rates and the same mean (mean t-max=0.495, s.e.=0.003; mean F-max=0.321, s.e.=0.003). In the case of correlated mating, we examined data simulated with either one sire (rp=1) or two sires (rp=0.5) per family for 15 outcrossing rates. We observed some bias in our estimates of t (Supplementary Table S5) although it is typically small. For example when true t=1, F=0, with rp=1, BORICE yielded t=0.97 and F=0.04 whereas with rp=0.5, BORICE yielded t=0.99 and F=0.00.

Application to Mimulus

From MLTR, estimated multilocus t for the SS population was 0.749 (s.e.=0.075) and estimated adult F was 0.341 (s.e.=0.164). The posterior distributions for t and F from BORICE are shown in Figure 3. Assuming no null alleles at these loci, the maximum posterior t was 0.62 (2.5 percentile=0.51, 97.5 percentile=0.75) and maximum posterior F was 0.19 (2.5 percentile=0.11, 97.5 percentile=0.30). The average ln likelihood for this model was −580.21. From these data, the relative fitness (ω) of selfed progeny was calculated as 0.76 (∂=0.23). Examining the posterior distributions of maternal inbreeding histories, we found that the most probable Ck=0 for most maternal plants. However, a few maternal plants had Ck=1 as the maximally probable value. Figure 4 illustrates the posterior distributions of inbreeding history for two maternal individuals, one outbred (Family 64) and one likely inbred (Family 25). Despite that the SS data set did not exhibit any ‘impossible genotypes’ in our initial model fitting, we also ran the model allowing null alleles at each locus. Allowing nulls altered the posterior distributions for t and F: the maximum t was 0.76 (2.5 percentile=0.62, 97.5 percentile=0.91) and maximum F was 0.13 (2.5 percentile=0.04, 97.5 percentile=0.23). The modal frequencies in the posterior distributions for null allele frequency were displaced from zero for loci 1 and 2. However, the average ln likelihood, −633.61, was substantially lower than the chain run without null alleles.

Figure 3
figure 3

Posterior distributions of estimated t (distribution on the right) and mean adult F (distribution to the left) for the SS population obtained using the BORICE software. The distributions consist of values of t and mean adult F from every 10 steps in the chain (total step length was 1 100 000) following the burn-in of 100 000 steps. For a given value of t or mean adult F on the x-axis, the corresponding value on the y-axis is the proportion of the chain yielding that t or mean adult F value.

Full size image
Figure 4
figure 4

Posterior distributions of inbreeding histories of two maternal individuals from the SS population obtained using the BORICE software. Family 64 (shown in white) represents an outbred maternal plant and Family 25 (shown in gray) an inbred maternal plant.

Full size image

Discussion

Measuring inbreeding depression in natural populations is critical to understanding mating system evolution, and perhaps also to conservation efforts. We suggest that the field-based method of Ritland (1990) has been under utilized in this effort. Ritland’s method requires accurate estimation of population t and adult F. The optimal allocation of effort for the joint estimation of t and F is different than the usual experimental design of mating system studies. Accurate inference of F requires sampling many families (maternal plants), which practically means fewer offspring per family. However, we have found that the most commonly used software to estimate t and F (MLTR) does not perform well with small family sizes unless the maternal genotype is known. In contrast, the Bayesian method executed in BORICE provides accurate joint estimates of population t and adult F for this situation.

The primary motivation for BORICE is to enable mating system studies with large numbers of families but small numbers of progeny per family, with subsequent estimation of inbreeding depression in situ. However, the platform may also prove useful if small families are an inherent feature of a species. Animal mating system studies commonly use single-generation approaches to estimate t and F because progeny arrays of sufficient size are rarely obtainable (Jarne and David, 2008). In this case, sampling of more families with fewer offspring per family is a natural experimental design and BORICE may here allow improved estimation.

BORICE characterizes the inbreeding history of the population with a set of latent variables. Each maternal plant has an inbreeding history value, Ck, which is the number of generations of selfing in its ancestry. This count determines the inbreeding coefficient of the maternal plant and hence the relative likelihood of inferred maternal genotypes. The posterior distributions for two Mimulus plants (Figure 4) illustrate how Ck is determined by progeny data when maternal genotypes are unavailable. In family 64, the progeny genotypes imply that the maternal plant must have been heterozygous at all three loci. Given allele frequencies, this strongly suggests that the maternal plant was outbred. In family 25, all four progeny were identically homozygous at the first two loci and three of four were homozygous at the third locus. The posteriors on maternal genotype strongly favored one homozygous genotype for each locus; an outcome most likely if the plant is inbred. Of course, with only three loci, conclusions about particular maternal plants are tentative. This data set is included here to illustrate the application of BORICE and not as a complete description of mating system in the SS population of M. guttatus.

Ck values are important determinants of the data likelihood, and hence the posterior distribution for t, but they are also variables of direct interest. Scofield and Schultz (2006) performed a meta-analysis of marker-based estimates for F and t. Their analysis suggested the provocative hypothesis that in mixed mating but long-lived plants, inbred plants never survive to adulthood. This conclusion follows from population mean F estimates for maternal plants that are close to zero, even in species with substantial selfing. However, strong conclusions about whether any inbred plants survive require inference of individual inbreeding histories. In our application to the SS population of M. guttatus, which is likely to be a short-lived perennial, the 95% credibility interval on F did not include zero and several maternal plants had posterior distributions for Ck suggesting they were inbred.

An important practical choice in applying BORICE is whether to allow null alleles at all marker loci, at a subset of loci, or at no loci. BORICE is not currently equipped with a formal model selection device. The Deviance Information Criterion is routinely used for model selection when posterior distributions are estimated using MCMC (Claeskens and Hjort, 2008), although it is unclear how to implement this calculation with categorical latent variables (maternal genotypes and inbreeding history values in the present application). Our simulations suggest a practical approach: If nulls are present at a locus but are excluded from the model, BORICE will routinely report impossible genotypes. In addition, allowing nulls routinely elevates the average ln likelihood when they are present in the data and the posterior distribution for null allele frequency will be displaced from zero. In contrast, if nulls are absent from the data but allowed in the model, the average ln likelihood is routinely lower for the more general (and in this case incorrect) model.

Does the evident bias in MLTR for small family sizes have implications for surveys of mating systems across angiosperms?

Virtually every plant mating system study has used MLTR to estimate t and/or adult F since its debut. After noting the MLTR bias for small families with an inferred maternal genotype, we conducted a literature search to examine if most applications were within or outside the region of bias. Using a database of published mating system papers up to the year 2006 (courtesy of Chris Eckert; modified from Goodwillie et al. (2005)), we identified observations based, on average per family, (1) more than eight progeny (and therefore largely outside the region of bias), or (2) fewer than eight progeny (that is, within the region of bias). Approximately 25 and 40% of the observations of t and F, respectively, fell within the region of bias (Table 2; Mean t=0.46, s.d.=0.41; Mean adult F=0.45, s.d.=0.32). Most estimates, however, were derived from progeny arrays of eight or more, and were therefore minimally biased (Mean t=0.71, s.d. of t=0.26; Mean adult F=0.03, s.d.=0.23). Far fewer studies reported F values from MLTR than reported t. Although we did not conduct an exhaustive literature search, it seems clear that most studies report unbiased estimates. However, future surveys of mating systems across angiosperms should take the MLTR bias into account when reporting estimates of t and adult F.

Table 2 Means and s.d. are reported for population outcrossing rate (t) and adult inbreeding coefficient (F) from a survey of published mating system studies that lacked maternal genotype information for progeny arrays
Full size table

Current limitations of BORICE and future work

The current version of BORICE is dedicated to a simple and specific mating system model. As noted above, we assume that all outcrossing is random and that the paternity of outcrossed seeds within a family are determined independently. The same underlying outcrossing rate is assumed for all maternal plants. We conducted simulations to determine whether biased results would be obtained from BORICE if these assumptions were violated. In the case of variation in outcrossing rate among maternal plants, we found little to no bias. We found slight bias in the estimate of the outcrossing rate with correlated matings, that is, when outcrossed progeny within a family are likely to be full siblings. In addition, we assume that inbreeding results from recurrent self-fertilization and biparental inbreeding does not take place. We intend to generalize BORICE allowing biparental inbreeding by replacing the discrete distribution for Ck with a continuous density for adult F values.

BORICE accommodates a systematic source of genotyping error, null alleles, but does not account for stochastic sources of genotyping error, such as spontaneous mutations, allelic dropout and false alleles. These types of genotyping error may be common, particularly when DNA is low in quantity or quality (Pompanon et al., 2005). A maximum likelihood method of identifying allelic dropout and false alleles is currently available (Johnson and Haydon, 2007). Furthermore, quality control methods should be put in place by researchers to identify stochastic genotyping errors during the experimental design and data collection phase (Pompanon et al., 2005; Guichoux et al., 2011). Thus, it should be possible for researchers to decide if particular loci should be excluded due to genotyping errors prior to using BORICE.

Data archiving

The BORICE software package is included here as supplementary files to the text. This includes the data set used for the empirical application of BORICE (serving as an example input datafile), as well as instructions for running BORICE. BORICE is also available upon request from the authors and will soon be available on a website to allow for easy download of future versions of BORICE. Questions on the installation and running of BORICE should be directed to Vanessa Koelling (vkoelling@ku.edu). In addition, the simulation data used to generate Table 1, Supplementary Tables S1–S5, and Figures 1 and 2, as well as the database of published mating system papers used in Table 2, have been deposited at Dryad: doi:10.5061/dryad.7455b.