Abstract
Given the drawbacks of implementing multivariate analysis for mapping multiple traits in genome-wide association study (GWAS), principal component analysis (PCA) has been widely used to generate independent ‘super traits’ from the original multivariate phenotypic traits for the univariate analysis. However, parameter estimates in this framework may not be the same as those from the joint analysis of all traits, leading to spurious linkage results. In this paper, we propose to perform the PCA for residual covariance matrix instead of the phenotypical covariance matrix, based on which multiple traits are transformed to a group of pseudo principal components. The PCA for residual covariance matrix allows analyzing each pseudo principal component separately. In addition, all parameter estimates are equivalent to those obtained from the joint multivariate analysis under a linear transformation. However, a fast least absolute shrinkage and selection operator (LASSO) for estimating the sparse oversaturated genetic model greatly reduces the computational costs of this procedure. Extensive simulations show statistical and computational efficiencies of the proposed method. We illustrate this method in a GWAS for 20 slaughtering traits and meat quality traits in beef cattle.
Similar content being viewed by others
Introduction
With the advance of high-throughput genotyping technology, the paradigm of mapping quantitative trait locus (QTL) based on the linkage analysis of sparse genetic markers has gradually shifted to genome-wide association studies (GWAS) based on thousands and thousands of single-nucleotide polymorphisms (SNPs). On the other hand, association studies tend to involve more than one quantitative traits or complex diseases located in different regions of chromosomes, allowing the investigation of common genetic risk factors underlying multiple traits. Although these traits could be analyzed separately with univariate genetic model, statistical methods and algorithms have been developed for simultaneously analyzing multiple normal traits (Jiang and Zeng, 1995; Fang et al., 2008; Ayroles et al., 2009; Zhu and Zhang, 2009; Stephens, 2010; Nadeau and Dudley, 2011; Shriner, 2012), multiple discrete traits (Lange and Whittaker, 2001; Xu et al., 2005; Yang et al., 2009) and multiple mixed traits of normal and discrete traits (Prentice and Zhao, 1991; Fitzmaurice and Laird, 1997; Liu et al., 2009).
With each quantitative trait being analyzed separately by the same genetic model, least squares estimation or maximum likelihood estimation gives the same genetic effect estimates as those from the joint analysis of multiple correlated trait. However, its significance test for QTL does not consider correlations among all the traits being analyzed. In contrast, jointly analyzing all correlated traits exhibits two distinct advantages. First, statistical power to detect QTL and the precision of parameter estimation (Jiang and Zeng, 1995; Zhu and Zhang, 2009) will be increased. Second, the complex statistical model leads to biologically meaningful conclusions, facilitating to address the issue of pleiotropy vs close linkage (Almasy et al., 1997; Liu et al., 2007) and to access the endophenotypes intermediate between a gene and a trait. Because of a large number of matrix calculations and the increased degrees of freedom of the test statistic (Weller et al., 1996), however, the multivariate analysis of all traits is extremely impractical when the number of quantitative traits is large. More recently, Verzilli et al. (2005) and Banerjee et al. (2008) employed seemingly unrelated regression model (Zellner, 1962) to map QTLs of correlated traits. With two multivariate models and the associated Bayesian algorithms, their modeling scheme outperforms the conventional multivariate model in terms of QTL identification.
When many correlated normal traits are collected, principal component analysis (PCA) and discriminant analysis are candidates to perform dimension reduction for these traits. By performing the PCA on all phenotypic traits based on their covariance matrix, a collection of the independent principal components of original traits, or ‘super traits’, could be obtained. Then a few leading principal components that explain the most variance of original phenotypes are chosen for separately mapping analysis (Weller et al., 1996; Mangin et al., 1998; Elston et al., 2000; Korol et al., 2001). With the regular PCA transformation, mapping results lack biological interpretability, as supper traits are a set of linear combinations of original traits. Although genetic effects of detected QTLs on super traits can always be back-transformed to those for original traits using the matrix of principal eigenvectors (Weller et al., 1996; Knott and Haley, 2000), this framework cannot produce equivalent parameter estimates to the joint analysis of original correlated traits. Specific to each tested position, the discriminant analysis can obtain one best linear combination of the traits from the estimated genetic and residual covariance matrices (Gilbert and Le Roy, 2003, 2004), improving the precision of parameter estimation and the statistical power of QTL detection.
A great volume of transcriptional expressions that are regarded as quantitative traits can be analyzed using the transcriptional expression QTL (eQTL) mapping aproaches (Brem et al., 2002; Schadt et al., 2003; Morley et al., 2004; Stranger et al., 2005; Wang et al., 2006). Several methods for eQTL mapping also motivate the modeling scheme of multiple quantitative trait mapping. By first clustering transcripts with similar expression into groups, sparse partial least-squares regression framework has been proposed to select markers associated with each cluster of genes (Chun and Keles, 2009). Adaptive multi-task least absolute shrinkage and selection operator (LASSO; Zhu et al., 2008) has been developed for detecting eQTLs that takes into account related expression traits simultaneously while incorporating many regulatory features. On the other hand, the graph-guided fused LASSO (Kim and Xing, 2009; Kim et al., 2009) considers regulatory networks over multiple expression traits within an association analysis, but previous knowledge on genomic locations is not incorporated. To date, however, most of the eQTL mapping approaches are still focusing on insufficient limited number of genetic markers from relatively small populations.
This article presents a statistical framework for analyzing many regular quantitative traits from GWAS, where a multivariate genetic model is constructed and each trait’s associations with all SNPs are tested using the same genetic model. An extremely fast LASSO (Yuan and Lin, 2005; Friedman et al., 2010) is employed to solve sparse oversaturated genetic model for each trait. Instead of working on principal components from phenotypic traits, this framework implements PCA for the estimated residual covariance matrix, so that multiple regular quantitative traits are transformed to a group of pseudo principal components or a group of pseudo traits. Based on this and the underlying transformation, the univariate analyses for pseudo traits give equivalent parameter estimates to joint multivariate analysis, but the computational burden for multiple quantitative traits mapping is largely reduced. Statistical and computational efficiencies of the proposed method are validated through extensive simulations and a real data set from a GWAS of 20 slaughtering traits and meat quality traits in beef cattle.
Method
Multivariate genetic model
In a GWAS involving multiple quantitative traits collected from a randomized population, t traits of interest are observed and m SNPs are genotyped on n subjects. By only considering the additive effects of SNPs, the phenotype of each trait can be partitioned into:

for i=1,2,···,n, l=1,2,···,t.
Where yil is the phenotypic value of the lth trait for the ith subject, βlj is the jth systemic environmental effect for the lth trait, xij is the incidence value for the ith subject in the jth systemic environmental effect, αlj is genetic effect of the jth marker on the lth trait, zij is the indicator variable of the jth marker for the ith subject, defined as 0 for heterozygote, −1 and 1 for the two homozygote, and eil is the residual error, which follows a multivariate normal distribution  with
with  being residual variance. We denote the simultaneous linear equations consisting of such models for t traits as the multivariate genetic model for mapping QTLs for multiple traits.
being residual variance. We denote the simultaneous linear equations consisting of such models for t traits as the multivariate genetic model for mapping QTLs for multiple traits.
With vector notation, model (1) is written as

with  ,
,  and
and  .
.
The expectation of yi is

and its covariance matrix is V(yi)=Σe.
Shrinkage estimation for genetic effects
As phenotypes are correlated with each other but independent among subjects, the likelihood function L is then the product of individual multivariate normal distribution density, or

Assuming μi is known, the maximum likelihood estimate of residual covariance matrix is given by

In general,  is positive definite, and thus can be decomposed into
is positive definite, and thus can be decomposed into

according to the Eigen decomposition, where V is the matrix of eigenvectors and Λ is a diagonal matrix consisting of eigenvalues. Let  and
and  , then the likelihood function becomes
, then the likelihood function becomes

where, δl is the lth eigenvalue along the diagonal of matrix Λ,  is defined as the lth pseudo principal component (or pseudo traits) for the ith subject and
is defined as the lth pseudo principal component (or pseudo traits) for the ith subject and  is the expected value of
is the expected value of  . As Equation (7), with this decomposition, can be partitioned into the product of t likelihood functions for t pseudo traits, the genetic model for each pseudo trait can be solved iteratively, although the pseudo traits may not be independent of each other. Based on this equivalent form of solution, the procedure could efficiently solve for genetic effects in the presence of multiple traits and a huge number of genetic markers. Nevertheless, when a fairly large number of traits are of interest, this procedure could focus on the first few leading pseudo traits, allowing reduction of computation costs in a lower-dimensional space.
. As Equation (7), with this decomposition, can be partitioned into the product of t likelihood functions for t pseudo traits, the genetic model for each pseudo trait can be solved iteratively, although the pseudo traits may not be independent of each other. Based on this equivalent form of solution, the procedure could efficiently solve for genetic effects in the presence of multiple traits and a huge number of genetic markers. Nevertheless, when a fairly large number of traits are of interest, this procedure could focus on the first few leading pseudo traits, allowing reduction of computation costs in a lower-dimensional space.
In particular, we implement penalized likelihood-based shrinkage estimation for each pseudo trait defined in Equation (7). With thousands and thousands of SNPs, the number of unknown parameters estimated in  is far greater than sample size, but the number of non-zero genetic effects is very small. Therefore, the LASSO regression with a coordinate descent step (Yuan and Lin, 2005; Friedman et al., 2010) can efficiently shrink most of genetic effects in
is far greater than sample size, but the number of non-zero genetic effects is very small. Therefore, the LASSO regression with a coordinate descent step (Yuan and Lin, 2005; Friedman et al., 2010) can efficiently shrink most of genetic effects in  to zeros in estimating the genetic effects associated with each pseudo trait. Denote the genetic effect of the jth SNP on the lth pseudo trait by
to zeros in estimating the genetic effects associated with each pseudo trait. Denote the genetic effect of the jth SNP on the lth pseudo trait by  , then the genetic effect
, then the genetic effect  is estimated by
is estimated by

for j=1,2,···, m and l=1,2,···, t′.
where, λ1 is a tuning parameter, which can be optimized with cross validation, and t′ is the total number of pseudo traits considered in the lower-dimensional space.
So far, we have outlined the statistical algorithms based on  , where the expectation μi of yi is still assumed to be unknown. As univariate analysis for model (1) gives identical point estimates of genetic effects to those from multivariate analysis, we solve the mean equation for each original trait separately to attain an estimate of Σe. Specifically, the LASSO regression (Yuan and Lin, 2005; Friedman et al., 2010) can be used to estimate the oversaturated model (1) and efficiently estimate systemic environmental effects as well as non-zero genetic effects by solving
, where the expectation μi of yi is still assumed to be unknown. As univariate analysis for model (1) gives identical point estimates of genetic effects to those from multivariate analysis, we solve the mean equation for each original trait separately to attain an estimate of Σe. Specifically, the LASSO regression (Yuan and Lin, 2005; Friedman et al., 2010) can be used to estimate the oversaturated model (1) and efficiently estimate systemic environmental effects as well as non-zero genetic effects by solving

where λ2 is a tuning parameter to be determined by cross validation. The estimated model leads to the estimated expectation μi of yi and then  .
.
To identify the genetic risk factors associated with multiple correlated traits, this framework transforms the phenotypic traits to a group of new traits using the eigenvectors of residuals covariance matrix. Approaching the problem in this way breaks down the complex problem into a sequence of analyzing individual pseudo trait separately. More importantly, it ensures the equivalency of parameter estimates between the two analysis frameworks. In sum, the parameter estimation can be implemented in the following steps:
-
1)
Estimate the expectation for each trait by solving the objective function (9).
-
2)
Calculate residual covariance matrix
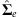 using (5).
using (5). -
3)
Decompose
 into VTΛV.
into VTΛV. -
4)
Determine the number of pseudo principal components being considered according to the cumulative proportion contributed by eigenvalues in matrix Λ.
-
5)
Generate the pseudo principal components by multiplying multiple phenotypes by a matrix of corresponding eigenvectors.
-
6)
Estimate non-zero genetic effects for each pseudo principal component by solving Equation (8).
Statistical inference for genetic effects
After the shrinkage estimation of genetic effects for each pseudo trait, the number of non-zero genetic effects is generally less than sample size. By directly applying ordinary least squares estimation, the systemic environmental effects and the non-zero genetic effects can be unbiasedly estimated for each pseudo trait as follows

for l=1,2,···,t′ and j=1,2,···,q, where q is the number of selected non-zero genetic effects.
Also, residual variance for each pseudo trait is estimated by

The variance-covariance matrix of the estimated parameters is then calculated by

Finally, the significance of non-zero genetic effects can be statistically tested based on Equations (10), (11) and (12), and SNPs corresponding to significant non-zero genetic effects are identified as the QTLs for the pseudo quantitative trait. In order to interpret the genetic effect on the quantitative trait measured in the original scale, the genetic effect associated with each detected QTL is transformed by

where νl is the eigenvector corresponding to the lth principal component in matrix V, and  is the jth estimated genetic effect for the lth pseudo trait.
is the jth estimated genetic effect for the lth pseudo trait.
Results
Simulated data
A total of 6000 SNPs with equal allele frequencies are simulated and evenly distributed across 6 chromosomes, with 1000 SNPs on each chromosome. Given constant correlations of 0.1 between two adjacent SNPs on the same chromosome, 6000 normally distributed random variables are first generated from a multivariate normal distribution with an expectation of 0 and given constant correlations. Then, indicator variable xij are generated as +1 if the random variable is >0.675, as −1 if it is <−0.675 and 0 otherwise. On each simulated chromosome, one or two SNPs (QTLs) are assumed to govern two normally distributed quantitative traits. The positions and genetic effects of 10 QTLs across 6 chromosomes are presented in Table 1. Residual variances for two traits are set to 1, so that residual covariance is equal to correlation between the two traits. With this setup, the heritabilities of 10 simulated QTLs range from 0 to 0.041 for the first trait and from 0 to 0.033 for the second trait. Phenotypic values are drawn from a bivariate normal distribution with the expectation μi and residual covariance matrix Σe, where the expectation μi can be calculated by the sum of the products of the simulated QTLs’ indicator variables and corresponding genetic effects. To evaluate influences of sample size and correlation between the two traits on mapping results, sample size is tested under two levels: 1000 and 2000, and correlation is set to one of four levels: 0, 0.2, 0.5 and 0.8.
The simulated data sets are analyzed by our proposed method (Residual PCA for short), joint analysis based on phenotypic PCA (Phenotypic PCA for short) and the conventional multivariate analysis scheme (Multivariate for short), respectively. To facilitate the comparison of the three analysis methods, all test statistics are transformed to –log(p) from the associated P-values. The simulations are repeated 500 times for estimating QTL parameters and accessing the statistical power of QTL detection. At 5% significance level, statistical power of QTL detection for each locus is calculated as the proportion of simulations where test statistic exceeds the critical value of 1.313. Also, false positive rate is evaluated with the 500 simulations under the null model without genetic effects on the two traits.
Table 2 shows the statistical power and false positive rate for QTL detections using the three analysis methods, and Table 3 reports the estimated QTL genetic effects when the correlation between two quantitative traits is 0.5. The results at other correlation levels are provided in Supplementary Tables S1–S4 of the Supplementary Material. In accordance with our expectations, each analysis method gives similar statistical patterns: (1) statistical power of QTL detection and the precision of parameter estimation increase as the QTL heritability increases, (2) statistical power of QTL detection is higher and false positive rate is lower as the QTL heritability increases and (3) large sample size is beneficial to identify QTL. All analysis methods are able to accurately find the simulated QTLs, with negligible deviations for positions. For various correlations between these two traits, Residual PCA method is basically identical to the joint analysis in terms of statistical power and QTL parameter estimation, but both methods distinctly outperform Phenotypic PCA method. In general, false positive rates are <10% for all scenarios. But Residual PCA method and Multivariate method deliver very similar false positive rates, which are clearly lower than those from the Phenotypic PCA method. Moreover, the relative statistical performance of these three analysis methods does not appear to depend on the correlation between the two traits. Although theoretically the estimates for QTL genetic effects should be the same between Multivariate method and Residual PCA method, minor discrepancies exist due to slightly different statistical powers of the two approaches.
We also record the computational time when implementing each analysis method for each simulated data set (results not shown). It can be seen that our proposed method takes almost the same computing time as that of Phenotypic PCA method, while Multivariate method takes about five times more computing time compared with our proposed method for sample size of 1000. As the sample size increases to 2000, the difference in computing time is further enlarged between our proposed method and the Multivariate method, suggesting the superior computational efficiency in additional to the statistical performance of the proposed approach.
Real data
Experimental population consists of 1058 young Simmental bulls born between 2008 and 2011, which are originated from Ulgai, Xilingol league, Inner Mongolia of China. After weaning, the cattle were moved to Beijing Jinweifuren cattle farm and were fattened under the same feeding and management environment. Growth and development traits for each individual were observed in a timely manner between 16 and 18 months old before slaughter. During the period of slaughter, carcass traits and meat quality traits were measured according to Institutional Meat Purchase Specifications for fresh beef guidelines. The blood samples were collected along with the regular quarantine inspection of the farms without the need of ethical approval. The DNAs were extracted from these blood samples using the routine procedures. The Illumina BovineHD BeadChip was adopted for quantifying and genotyping DNAs.
Before statistical analysis, SNPs were removed from the study if (1) their call rates are <90%, (2) minor allele frequency are <3% or (3) genotype appearance are <5 individuals or if they are departing from Hardy–Weinberg equilibrium with P-values <10−6. In addition, individuals with >10% missing genotypes or with >2% Mendelian error rates in genotyping are excluded. Finally, a total of 986 individuals and 631 396 SNPs were collected for the multiple-trait GWAS analysis.
Among a total of 40 carcass traits and meat quality traits, 20 are chosen to demonstrate the proposed method. These analyzed traits include live weight, carcass weight, net weight of beef (boneless), net weight of beef, head weight, forehoof weight, cowhide weight, oxtail weight, flank weight, ribeye weight, high rib weight, tenderloin weight, shin weight, shoulder weight, topside weight, silverside weight, top round weight, rump weight, shank weight and hoof weight. Phenotypic correlations among these traits, listed in Supplementary Table S5, are >0.40.
Environmental factors, such as measuring year and slaughtering age (in months), are included in the genetic model, and population stratification is taken into account as well. In the shrinkage estimation of genetic model for each trait, fold numbers for cross-validations are set from 3 to 10 to make sure each trait has non-zero genetic effect after shrinkage. Then pseudo traits in a lower-dimensional space are obtained by performing PCA on the residual covariance matrix as discussed in ‘Method’ section. The first two pseudo traits are analyzed, which together explain >85% of the residual covariance matrix variation.
At significance level of 0.05, 27 significant SNPs are identified as the QTLs for the first two pseudo traits. But for the clarity of tabulating mapping results, we report 14 SNPs out of these 27 detected SNPs in Table 4 by having a significance level of 0.001. As can be seen from Table 4, the heritabilities of these detected QTLs are overall very low for two pseudo traits, ranging from 0.00 to 0.13. The genetic effects of these detected QTLs are transformed to those for 20 original traits by eigenvectors corresponding to each pseudo principal components. The results provided in Supplementary Table S6 of Supplementary Material show that many genetic effects are small and even negligible. However, absolute values of genetic effects can not precisely reflect the impact of detectable SNPs on any original trait, as heritability also depends on each trait’s phenotypic variation. In fact, the heritabilities of detected QTLs on 20 analyzed traits can be calculated from the estimated genetic effects and the estimated residual variances, where the latter one can be estimated by diag (VTΛV) for original traits. It can be seen from Table 5 that, in general, the thirteenth and fourteenth QTLs have higher genetic influence on the analyzed traits than other detectable QTLs. Further, the heritability of QTL can also be used to indicate the extent to which the pleiotropy occurs.
Discussion
In the conventional phenotypic PCA for analyzing multiple traits, phenotypic covariance matrix Σp is firstly decomposed into  and then phenotypes of multiple traits are orthogonally transformed to independent principal components through eigenvector matrix Vp. As Vp is an orthogonal matrix, the relationship between phenotypes (yi) and principal components (CPi) can be described as CPi=Vpyi and
and then phenotypes of multiple traits are orthogonally transformed to independent principal components through eigenvector matrix Vp. As Vp is an orthogonal matrix, the relationship between phenotypes (yi) and principal components (CPi) can be described as CPi=Vpyi and  . Substituting
. Substituting  into likelihood function (4) gives
into likelihood function (4) gives

Obviously, this likelihood function cannot be solved sequentially for principal components, because  is a non-diagonal matrix. But if Σe=Σp, then
is a non-diagonal matrix. But if Σe=Σp, then  with Λp being a diagonal matrix consisting of eigenvalues. This assumption, however, holds only in the case of no pleiotropic or closely linked QTLs for multiple traits. In contrast, our proposed method based on the PCA for residual covariance matrix is more general, which factorizes the likelihood function for multiple traits into multiple independent likelihoods for all pseudo principal components or pseudo traits. As a result, univariate analyses for pseudo traits give equivalent parameter estimates to the joint multivariate analysis under a linear transformation.
with Λp being a diagonal matrix consisting of eigenvalues. This assumption, however, holds only in the case of no pleiotropic or closely linked QTLs for multiple traits. In contrast, our proposed method based on the PCA for residual covariance matrix is more general, which factorizes the likelihood function for multiple traits into multiple independent likelihoods for all pseudo principal components or pseudo traits. As a result, univariate analyses for pseudo traits give equivalent parameter estimates to the joint multivariate analysis under a linear transformation.
The key to implement the proposed method is the estimation of unknown residual covariance matrix. According to the equivalency of maximum likelihood estimate between univariate analyses and the joint analysis for the model (1) with the same genetic model for each trait, the residual covariance matrix in this study is estimated through the maximum likelihood estimation of genetic model for each trait. Note that the LASSO procedure (Yuan and Lin, 2005; Friedman et al., 2010) for estimating the sparse oversaturated genetic model for each trait leads to biased non-zero genetic effects due to forcing penalties, and the biased estimates for genetic effects are associated with the biased estimates of residual covariance matrix. However, by initializing with its biased estimate, residual covariance matrix could be iteratively estimated along with all other genetic effects. This iterative process can be carried out from step (2) to step (5) in the outlined algorithm. We investigate the performance of this iteration scheme using the simulated data set (results not shown) and find that iteration runs less than five times to converge, and mapping results are basically the same as those without iterations.
For detecting genetic variations associated with beef carcass traits and meat quantity traits, GWAS have been conducted in Korean Hanwoo cattle (Lee et al., 2010), Korean beef cattle (Kim et al., 2011) and Australian taurine and indicine cattle (Bolormaa et al., 2011). Many significant SNPs were identified using the simple linear regression and stepwise regression procedures. Bolormaa et al. (2010) carried out a multiple-trait GWAS for dairy traits using a PCA and a series of bivariate analyses. In this article, it is shown that multiple-trait GWAS has better statistical power to detect associations than single-trait GWAS and to identify additional associations without an increased false discovery rate. However, it did not increase the precision for the mapped QTL. Until now, no GWAS based on PCA has been reported for multiple beef carcass traits and meat quantity traits, and <50 000 SNPs were used in the previous GWAS in cattle. With a total of 630 000 SNPs in our study, it is expected that more biologically important SNPs are identified. This will largely improve our knowledge of the genetic architecture of beef traits and provide a valuable research tool for analyzing multiple traits in other GWAS.
Data archiving
Data available from the Dryad Digital Repository: 10.5061/dryad.mh77c.
References
Almasy L, Dyer TD, Blangero J . (1997). Bivariate quantitative trait linkage analysis: pleiotropy versus co-incident linkages. Genet Epidemiol 14: 953–958.
Ayroles JF, Carbone MA, Stone EA, Jordan KW, Lyman RF, Magwire MM et al. (2009). Systems genetics of complex traits in Drosophila melanogaster. Nat Genet 41: 299–307.
Banerjee S, Yandell BS, Yi N . (2008). Bayesian quantitative trait loci mapping for multiple traits. Genetics 179: 2275–2289.
Bolormaa S, Neto LR, Zhang YD, Bunch RJ, Harrison BE, Goddard ME et al. (2011). A genome-wide association study of meat and carcass traits in Australian cattle. J Anim Sci 89: 2297–2309.
Bolormaa S, Pryce JE, Hayes BJ, Goddard ME . (2010). Multivariate analysis of a genome-wide association study in dairy cattle. J Dairy Sci 93: 3818–3833.
Brem RB, Yvert G, Clinton R, Kruglyak L . (2002). Genetic dissection of transcriptional regulation in budding yeast. Science 296: 752–755.
Chun H, Keles S . (2009). Expression quantitative trait loci mapping with multivariate sparse partial least squares regression. Genetics 182: 79–90.
Elston RC, Buxbaum S, Jacobs KB, Olson JM . (2000). Haseman and Elston revisited. Genet Epidemiol 19: 1–17.
Fang M, Jiang D, Pu L, Gao H, Ji P, Wang H et al. (2008). Multitrait analysis of quantitative trait loci using Bayesian composite space approach. BMC Genet 9: 1–11.
Fitzmaurice GM, Laird NM . (1997). Regression models for mixed discrete and continuous responses with potentially missing values. Biometrics 53: 110–122.
Friedman J, Hastie T, Tibshirani R . (2010). Regularization paths for generalized linear models via coordinate descent. J Stat Softw 33: 1–22.
Gilbert H, Le Roy P . (2003). Comparison of three multitrait methods for QTL detection. Genet Sel Evol 35: 281–304.
Gilbert H, Le Roy P . (2004). Power of three multitrait methods for QTL detection in crossbred populations. Genet Sel Evol 36: 347–361.
Jiang C, Zeng ZB . (1995). Multiple trait analysis of genetic mapping for quantitative trait loci. Genetics 140: 1111–1127.
Kim S, Sohn KA, Xing EP . (2009). A multivariate regression approach to association analysis of a quantitative trait network. Bioinformatics 25: i204–i212.
Kim S, Xing EP . (2009). Statistical estimation of correlated genome associations to a quantitative trait network. PLoS Genet 5: e1000587.
Kim Y, Ryu J, Woo J, Kim JB, Kim CY, Lee C . (2011). Genome-wide association study reveals five nucleotide sequence variants for carcass traits in beef cattle. Anim Genet 42: 361–365.
Knott SA, Haley CS . (2000). Multitrait least squares for quantitative trait loci detection. Genetics 156: 899–911.
Korol AB, Ronin YI, Itskovich AM, Peng J, Nevo E . (2001). Enhanced efficiency of quantitative trait loci mapping analysis based on multivariate complexes of quantitative traits. Genetics 157: 1789–1803.
Lange C, Whittaker JC . (2001). Mapping quantitative trait loci using generalized estimating equations. Genetics 159: 1325–1337.
Lee YM, Han CM, Li Y, Lee JJ, Kim LH, Kim JH et al. (2010). A whole genome association study to detect single nucleotide polymorphisms for carcass traits in Hanwoo populations. Asian Australas J Anim Sci 23: 417–424.
Liu J, Liu Y, Liu X, Deng H-W . (2007). Bayesian mapping of quantitative trait loci for multiple complex traits with the use of variance components. Am J Hum Genet 81: 304–320.
Liu J, Pei Y, Papasian CJ, Deng HW . (2009). Bivariate association analyses for the mixture of continuous and binary traits with the use of extended generalized estimating equations. Genet Epidemiol 33: 217–227.
Mangin B, Thoquet P, Grimsley N . (1998). Pleiotropic QTL analysis. Biometrics 54: 89–99.
Morley M, Molony CM, Weber TM, Devlin JL, Ewens KG, Spielman RS et al. (2004). Genetic analysis of genome-wide variation in human gene expression. Nature 430: 743–747.
Nadeau JH, Dudley AM . (2011). Systems genetics. Science 331: 1015–1016.
Prentice RL, Zhao LP . (1991). Estimating equations for parameters in means and covariances of multivariate discrete and continuous responses. Biometrics 47: 825–839.
Schadt EE, Monks SA, Drake TA, Lusis AJ, Che N, Colinayo V et al. (2003). Genetics of gene expression surveyed in maize, mouse and man. Nature 422: 297–302.
Shriner D . (2012). Moving towards system genetics through multiple trait analysis in genome-wide association studies. Front Genet 3: 1.
Stephens M . (2010) ‘A unified framework for testing multiple phenotypes for association with genetic variants’. 60th Annual Meeting of the American Society of Human Genetics, Washington, DC.
Stranger BE, Forrest MS, Clark AG, Minichiello MJ, Deutsch S, Lyle R et al. (2005). Genome-wide associations of gene expression variation in humans. PLoS Genet 1: e78.
Verzilli CJ, Stallard N, Whittaker JC . (2005). Bayesian modelling of multivariate quantitative traits using seemingly unrelated regressions. Genet Epidemiol 28: 313–325.
Wang S, Yehya N, Schadt EE, Wang H, Drake TA, Lusis AJ . (2006). Genetic and genomic analysis of a fat mass trait with complex inheritance reveals marked sex specificity. PLoS Genet 2: e15.
Weller JI, Wiggans GR, Vanraden PM, Ron M . (1996). Application of a canonical transformation to detection of quantitative trait loci with the aid of genetic markers in a multi-trait experiment. Theor Appl Genet 92: 998–1002.
Xu C, Li Z, Xu S . (2005). Joint mapping of quantitative trait Loci for multiple binary characters. Genetics 169: 1045–1059.
Yang F, Tang Z, Deng H . (2009). Bivariate association analysis for quantitative traits using generalized estimation equation. J Genet Genomics 36: 733–743.
Yuan M, Lin Y . (2005). Efficient empirical Bayes variable selection and estimation in linear models. J Am Stat Assoc 100: 1215–1225.
Zellner A . (1962). An efficient method of estimating seemingly unrelated regressions and tests for aggregation bias. J Am Stat Assoc 57: 348–368.
Zhu J, Zhang B, Smith EN, Drees B, Brem RB, Kruglyak L et al. (2008). Integrating large-scale functional genomic data to dissect the complexity of yeast regulatory networks. Nat Genet 40: 854–861.
Zhu W, Zhang H . (2009). Why do we test multiple traits in genetic association studies? J Korean Stat Soc 38: 1–10.
Acknowledgements
This work is partially supported by the National Natural Science Foundations of China (30972077 and 31172190).
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Competing interests
The authors declare no conflict of interest.
Additional information
Supplementary Information accompanies this paper on Heredity website
Supplementary information
Rights and permissions
About this article
Cite this article
Gao, H., Zhang, T., Wu, Y. et al. Multiple-trait genome-wide association study based on principal component analysis for residual covariance matrix. Heredity 113, 526–532 (2014). https://doi.org/10.1038/hdy.2014.57
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/hdy.2014.57


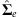 using (5).
using (5).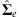 into VTΛV.
into VTΛV.