Introduction

Product release from enzyme active sites is often reversible and rebinding is common in many enzyme systems1,2,3,4. Liberated product(s) can effectively compete with substrate binding to enzyme active sites and inhibit enzyme cycling. Such product inhibition generates non-linearity in steady-state time courses of enzyme-catalyzed product formation, which limits the utility of established approaches developed under the assumptions of irreversible product dissociation and constant substrate concentration.

The important enzyme cycling kinetic parameters, kcat and Km, represent the maximal enzyme turnover rate and substrate concentration-dependence of enzyme activation respectively and define an enzyme's performance, specificity, efficiency and proficiency5,6. These parameters can in principle be obtained from analyzing non-linear time courses displaying product inhibition (and/or substrate depletion). However, complex non-linear rate equations and their integrations render such analysis laborious and impractical for most investigators working on enzymes and their catalyzed reactions. Instead, interference from product inhibition during steady-state enzyme cycling is deliberately avoided by limiting analysis exclusively to initial velocities determined at early time regimes of product formation3,5,6,7,8,9,10,11, or through the use of coupled enzyme assays that catalytically remove product12,13,14. However, such experimental modifications may be subject to large uncertainty, particularly if they do not eliminate the factors contributing to product inhibition. For example, enzymes that bind product(s) with higher affinity than substrate are not readily amenable to analysis of initial velocities13,15,16,17 and enzymes that binds product(s) tightly13,18 can effectively compete with coupled assays at removing product from catalytic reaction, rendering such strategies inefficient13. Single turnover kinetic analysis19 can overcome the difficulties of product inhibition, but such measurements typically require prohibitively high enzyme concentrations, particularly if substrate binding is weak. Such cases inevitably require analysis of the entire non-linear time course of steady-state product formation, explicitly accounting for contributions arising from product inhibition and/or substrate depletion13,20,21,22,23,24.

Numerous efforts have aimed to develop methods of enzyme kinetic analysis accounting for product inhibition4,5,20,25,26,27,28,29,30,31,32,33,34,35,36,37. However, no general, direct and practical method of extracting enzyme cycling parameters from non-linear time courses has resulted from these efforts8,21,22,36. For example, the integrated form of the rate equation employed in the pioneering works of Henri38 and Michaelis and Menten6,11 considers product inhibition, but it is a complex implicit function of time with superposition of a linear and a logarithmic function that pose extreme challenges in curve fitting even with modern computers. In addition, many of these analyses assume product(s) bind reversibly, individually and exclusively to free enzyme in an off-pathway reaction6,11,38. However, multiple products can also bind simultaneously (e.g. ADP and Pi of an ATPase) and product rebinding to an enzyme's active site in most cases is on-pathway.

A practical approach for analysis of non-linear enzyme activity time courses with product inhibition and/or substrate depletion involves numerical integration of rate equations using kinetic simulations6,39,40. Global fitting and kinetic simulations can potentially reveal the fundamental rate and equilibrium constants of multi-step pathways such as those of enzyme catalyzed reactions without the need for assumptions to simplify analysis or derivation and analytical integration of rate equations40. However, such simulations do not explicitly provide the familiar enzyme cycling parameters of interest (e.g. kcat and KM) and the utility of kinetic simulations can be restricted by a lack of investigator knowledge of the catalytic pathway(s). Specifically, calculation of kcat and KM values from intrinsic rate constants requires knowledge of the reaction mechanism since the kcat and KM are composites of the elementary reaction constants and thus vary among different enzyme mechanisms14,17,41,42,43. In addition, simulations rarely if ever yield unique solutions and require independent measurements of reaction constants to constrain free parameters during fitting40. As such, analysis of non-linear enzyme activity time courses is a challenge. It would be very useful to determine enzyme cycling parameters more accurately while providing more information (e.g. the extent of product inhibition) if practical methods of analysis were available to extract initial velocity and product inhibition parameters directly from full non-linear enzyme activity time courses.

Here we present a simple and practical method for determining enzyme cycling parameters from enzyme activity time courses displaying non-linearity due to product inhibition and/or substrate depletion. In the Supplementary Information, we provide the theoretical derivation of the exact solution and first and second order mathematical approximations of the exact solution of the non-linear product formation rate equation describing enzyme cycling, accounting for product inhibition as well as substrate depletion. The integrated forms of the rate equation allows for fitting of non-linear kinetic time courses, thereby permitting extraction of initial enzyme velocities and de-convolution of product inhibition and substrate depletion simultaneously. Since the first order approximation has proven in our hands to converge rapidly in practice, here we focus on implementation of the first order approximation to the analytical solution. The method described is general under the first order approximation condition (see Discussion) and can be used for all enzyme systems independent of reaction schemes. For cases where the first order approximation is inadequate, we also provide mathematical equation of the second order approximation (Supplementary Information).

Results

The following equation (Eq. 1; from Eq. A23 derived in Supplementary Information) describes time courses of steady-state enzyme-catalyzed product ([P]) formation and can be used to fit both linear and non-linear, steady-state enzyme kinetic time (t) courses (Figures 1A and 2A):

The fits of the data with Eq. 1 yield two parameters: v0, the initial enzyme cycling velocity (e.g. no product inhibition or substrate depletion); and η, a new term describing the reduction in cycling velocity that causes non-linearity in time courses. This term is the relaxation rate constant of v0 and when time courses become linear at η ~ 0, Eq. 1 simplifies to the familiar [P] = v0t. The initial velocity (v0) values as a function of substrate concentration are used to determine the steady-state cycling parameters, kcat and KM, according to established formalisms5.

Figure 1
figure 1

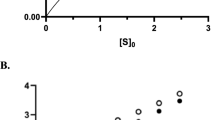
Analysis of Michaelis' and Menten's experimental data.

(A). Time courses of product formation from Michaelis' and Menten's experiment 1 at [S]0 of 0.333 ( black), 0.167 ( red), 0.0833 ( blue), 0.0416 ( magenta), 0.0208 ( olive), 0.0104 ( navy) and 0.0052 M ( violet). The solid lines through the data points represent the best-fits to the product inhibition/substrate depletion equation (Eq. 1). Data at times longer than 150 min were also included in the fit but are not shown for clarity. (B). [S]0-dependence of the initial enzyme cycling velocity (filled black circles) with the standard error (black bars) obtained from the best-fits shown in Figure 1A. The initial velocities (filled cyan stars) obtained by Michaelis and Menten from fitting data points acquired at an early time regime to a straight line are also plotted for comparison. To convert the observed optical rotation change to product concentration, we used the following relation derived from the conversion used by Michaelis and Menten: change in optical rotation = 1.313 m° = 55.62° M−1 m° = 42.36° M−1 is the optical rotation of one molar sucrose substrate, obtained by linear fit of the optical rotation vs. initial sucrose substrate concentration (t = 0) according to Table 1 in Michaelis' and Menten's original paper6,11. The solid line represents the best-fit to a rectangular hyperbola (Eq. A9), yielding values for Vm (i.e. kcat[E]tot) = 0.73 (±0.03) mM min−1, KM = 13 (±3) mM and Vm/KM = 0.055 (±0.0006) min−1, similar to the Vm = 0.76 (±0.05) mM min−1, KM = 16.7 mM and Vm/KM = 0.0454 (±0.0032) min−1 reported by Michaelis and Menten6,11. Uncertainty bars in Panels B and C represent the standard errors from the corresponding fits. (C). [S]0-dependent enzyme cycling velocity reduction rate constant η. The solid line through the data points is for visualization only. Substrate concentration regimes where time courses will display linear and non-linear behavior are indicated.

Full size image
Figure 2
figure 2

Analysis of non-linear enzyme kinetic time courses.

(A). Simulated enzyme cycling time courses according to Figure A1 with initial [substrate] (from bottom to top) of 10, 20, 40, 80, 160, 320, 640 and 1280 μM and the following fundamental reaction rate constants: k+1 = 0.06 μM s−1, k−1 = 25 s−1, k+2 = 0.1 s−1, k−2 = 0.3 s−1, k+3 = 10 s−1, k−3 = 1 μM s−1, k+4 = 10 s−1, k−4 = 0.1 μM s−1, k+5 = 10 s−1, k−5 = 0.1 μM s−1, k+6 = 9.7 s−1 and k−6 = 0.8 μM s−1. The solid lines through the simulated data represent the best-fits to the product inhibition/substrate depletion equation (Eq. 1). (B). [S]0-dependence of the initial enzyme cycling velocity. The solid line represents the best-fit to a rectangular hyperbola (Eq. A9), yielding values of Vm = 0.098 (±0.0005) μM s−1, KM = 442.8 (±4) μM, which agree well to the values of Vm = 0.097 μM s−1, KM = 412.2 μM predicted from the fundamental rate constants (Eq. A10). (C). [S]0-dependent enzyme cycling velocity reduction rate constant η. The solid line through the data points is for visualization only. Substrate concentration regimes where time courses will display linear and non-linear behavior are indicated.

Full size image

The value of η varies with substrate concentration and indicates the extent of non-linearity in enzyme activity time courses, while serving as a valuable diagnostic parameter to de-convolute the contributions of product inhibition and substrate depletion. Values of η > τ −1, where τ is the time range of data acquisition, characterize non-linear time courses and indicate that product inhibition and/or substrate depletion are contributing significantly to the observed data set. Conversely, values of η ≪ τ −1, indicate linearity and fulfillment of the initial velocity approximation commonly used in steady-state enzyme kinetic analysis. The substrate concentration-dependence of η reveals the origins of non-linearity – values of η that decrease with substrate concentration reflect a regime where substrate depletion dominates, while values of η that increase with substrate concentration indicate a regime where product inhibition dominates (see Supplementary Information). Values of η > τ −1 that vary little with substrate concentration arise when both product inhibition and substrate depletion contribute similarly to the degree of observed nonlinearity in enzyme cycling kinetics. Note that η ∝ [E]tot, which quantitatively predicts how reducing the enzyme concentration reduces both substrate depletion and product inhibition effects.

As an example demonstrating the utility and simplicity of this analysis method, we reanalyze Michaelis' and Menten's original data of invertase-catalyzed hydrolysis of sucrose to fructose and glucose6,11. Michaelis' and Menten's published data6,11 are well fitted to the transient product formation equation developed here (Eq. 1; Figure 1A). The initial velocities (v0) obtained from fitting data to Eq. 1 (black filled circles) match those obtained by Michaelis and Menten (filled cyan stars) at small and large substrate concentrations when the time courses have less curvature. Conversely, at intermediate substrate concentrations, where the time courses display large curvature (Figure 1B), the initial velocities obtained with our approach are slightly higher than those determined by Michaelis and Menten. This is understandable, given that when drawing a straight line through approximately linear data points at early time to determine the initial velocity, it is difficult to avoid underestimation when the time course curvature is large. The steady-state cycling parameters, kcat and KM, determined from the substrate concentration-dependence of the initial velocity (v0) are comparable to those of Michaelis and Menten (Figure 1B). However, because the non-linearity in Michaelis and Menten's data occurs at low substrate concentrations and diminishes at high substrate (Figures 1A and 1C), the majority of non-linearity in the data originates from substrate depletion rather than product inhibition, as the authors originally concluded6,11.

To demonstrate the robustness and accuracy of the technique, we also analyze simulated data of a multi-step enzyme reaction pathway (Figure A1 in Supplementary Information) with arbitrarily assigned reaction rate constants. The steady-state cycling parameters obtained from analysis of the non-linear time courses with Eq. 1 (Figures 2A and 2B), yield essentially identical values as predicted from theory (Eq. A10 in Supplementary Information) and the reaction rate constants. Non-linearity in this case originates predominantly from product inhibition (i.e., η < τ −1 at low substrate concentrations progresses to η > τ −1 at higher substrate concentration; Figure 2C).

Analysis of non-linear, steady-state kinetic time courses by this method permits determination of the product binding affinity, according to established protocols of enzyme inhibition5 (here the product is acting as an enzyme inhibitor) without the need for additional experiments. To do this, one must first plot the velocity versus substrate concentration at different product concentrations (Figure 3). These plots can be readily generated by using the following observed velocity (vobs) equation (Eq. 2; Eq. A28 in Supplementary Information):

where the v0 and η values are obtained from analysis of non-linear product formation time courses with Eq. 1. We generated such plots of observed velocity (vobs) versus initial substrate concentration using Michaelis and Menten's original data (Figure 1) at [P] = 0 and 5 mM (Figure 3A). Following established analysis methods of steady-state enzyme inhibition5, global fitting of the two data sets (Figure 3A) was performed to the following equation for mixed (competitive and uncompetitive) inhibition by a single inhibitor while accounting for substrate mass conservation ([S] = [S]0 − [P])5:

With fixed [P] values and unconstrained competitive inhibition binding constant Kic, uncompetitive inhibition constant Kiu, maximal velocity Vm and KM values, the global fit yields Kic = 47 (±9) mM and Kiu ~ 300 mM. The latter is very weak, indicating product inhibition originates exclusively from competitive binding with substrate.

Figure 3
figure 3

Analysis of product binding and inhibition.

[S]0-dependence of enzyme cycling velocity calculated according to Eq. 2 at product concentrations of: panel A. 0 and 5 mM for Michaelis and Menten's data from Figure 1A; and panel B. 0 and 3.5 μM for the simulated time courses presented in Figure 2A. The smooth lines through the data points represent the best fits to the mixed inhibition equation (Eq. 3).

Full size image

In separate experiments, Michaelis and Menten determined enzyme-product binding affinities of 58 mM (fructose, KP1) and 88 mM (glucose, KP2)6,11. The overall affinity of the two products (KP1P2, under conditions of [P1] ~ [P2] ≫ [E]), can be calculated with the following equation:

Using Michaelis and Menten's measured product affinities, the calculated KP1P2 is 70 mM, which is about 1.5 fold greater than the Kic value of 47 (±9) mM obtained using the method described above with Eq. 3. The fact that the obtained Kic value agrees well with the binding affinities of 58 mM for fructose almost within the uncertainty indicates that inhibition by two competing products is dominated by the one with tighter affinity.

Similarly, we also produced plots of observed velocity (vobs) versus initial substrate concentration using Eq. 2 for the simulated data (Figure 2) at two product concentrations [P] = 0 and 3.5 μM; (Figure 3B). Global fitting of the two curves (Eq. 3) yields Kic = 7.5 (±0.6) μM, which is more than two folder tighter than the overall affinity of 21.4 μM for the two products binding to the enzyme calculated (Eq. 4) from the individual binding affinities of 12 μM (k+6/k−6) and 100 μM (k+4/k−4) (Figure 3B and Supplementary Information Figure A1), but agrees reasonably well with the tighter affinity of the two. The extremely weak uncompetitive binding affinity (Kiu) of 3 × 1018 μM obtained from global fitting is consistent with the lack of an enzyme-substrate-product state in the scheme on which the simulated data is based (Supplementary Information Figure A1).

Discussion

The general method described here provides a direct and practical approach to analyze nonlinear enzyme kinetic time courses with contributions from product inhibition and/or substrate depletion, independent of the specific enzyme reaction mechanism and catalytic pathway. Compared to other integrated forms of the nonlinear rate equation used to analyze entire, non-linear enzyme kinetic time courses4,5,6,11,20,25,26,27,28,29,30,31,32,33,34,35,36,37, the method described here is practical and straightforward to use and rapidly converges during parameter optimization in data analysis. The method extracts meaningful enzyme cycling kinetic (kcat and KM) parameters from entire non-linear time courses, which is more accurate than analysis of early time points based on the initial velocity assumption with little product formation3,5,6,7,8,9,10,11. Moreover, the method reveals the origin of nonlinearity in enzyme kinetic time courses and provides the overall product binding affinity of the enzyme. As such, the formalism based on determining the true initial velocity and the parameter η from analysis of full time courses provides physically meaningful interpretations of observed nonlinearity in enzyme cycling time courses.

The first order approximation of the exact solution of the non-linear rate equation implemented here simplifies the complicated time-dependent change in enzyme cycling rate to an exponential function. When the product concentration is much smaller than the initial substrate concentration (i.e. [P] ≪ [S]0), as is commonly the case in the experimentally observed region of steady-state time courses, the change in turnover rate follows an exponential decay and the first order approximation is reliable. In cases where the decay in turnover rate deviates from an exponential, the second order approximation (presented in the Supplementary) or higher may be required for analysis. For example, when the Km for substrate catalysis is much tighter than product(s) binding affinity and the time courses are exceedingly long such that most of the substrate is converted to product, higher order corrections may be needed.

We emphasize here that the method introduced here is applicable only for steady-state enzyme activity (i.e. the system must have achieved more than one turnover per enzyme). Accordingly, pre-steady-state/transient kinetic behaviors, including burst and lag phases, are not described by the method presented in this work. Similarly, the approach does not apply to the cases where enzyme-catalyzed reaction time courses do not reflect the steady-state behavior of the enzyme under study (e.g., deficiencies in coupled assays used for detection, which must be carefully evaluated with appropriate control experiments44).

Methods

Kinetic simulations were performed with Tenua (available free at http://bililite.com/tenua/) or Kintek Global Kinetic Explorer (Kintek Co., Texas). Curve-fitting was carried out with software Origin (www.originlab.com).