Search
Close
Search
Advanced Search
Search Menu

Abstract

Biomarker use in exposure assessment is increasingly common, and consideration of related issues is of growing importance. Exposure quantification may be compromised when measurement is subject to a lower threshold. Statistical modeling of such data requires a decision regarding the handling of such readings. Various authors have considered this problem. In the context of linear regression analysis, Richardson and Ciampi (Am J Epidemiol 2003;157:355–63) proposed replacement of data below a threshold by a constant equal to the expectation for such data to yield unbiased estimates. Use of such an imputation has some limitations; distributional assumptions are required, and bias reduction in estimation of regression parameters is asymptotic, thereby presenting concerns about small studies. In this paper, the authors propose distribution-free methods for managing values below detection limits and evaluate the biases that may result when exposure measurement is constrained by a lower threshold. The authors utilize an analytical approach and a simulation study to assess the effects of the proposed replacement method on estimates. These results may inform decisions regarding analytical plans for future studies and provide a possible explanation for some amount of the discordance seen in extant literature.

bias (epidemiology), censored data, epidemiology, molecular, limit of detection, regression analysis
dl, detection limit, ND, “nondetects.”

The growing use of biomarkers in exposure assessment suggests the need to address issues related to their measurement. Even when levels are sufficient for measurement, some random exposure measurement error is expected, in part related to instrument precision. However, in many cases a proportion of study participants have levels at or below some experimentally determined detection limit (dl). Investigators are often interested in the risk of negative health outcomes associated with such levels. For example, studies of serum organochlorine levels, lipophilic xenobiotics, and breast cancer have determined that up to 99 percent of study participants have levels below the dl for some toxicants under study (1).

Biomarker quantification may be compromised if instrumentation cannot detect low levels. This may occur, for example, in quantitation of immunoassays (e.g., enzyme-linked immunosorbent assays) that require antigen concentrations sufficient for binding by antibodies. Highly specific binding conditions may impair antibody sensitivity and thereby challenge quantitation of low levels (2). Alternatively, assays may detect low biomarker levels but suffer from insufficient specificity, and measurement of exposure is hampered by background. The detection limit is often determined as a function of observed variance for a series of blanks; the terms “limit of detection” and “limit of quantification” generally correspond to three and 10, respectively, standard deviations from serial measurement of blanks (3). As such, numerical data are observable above and below the dl; even among values above the threshold, it may not be possible to clearly delineate between those that are “real” and those that are not. Data below the threshold are often reported by laboratories as “nondetects,” and the data analyst or epidemiologist is limited to this qualitative assessment.

Statistical modeling of these data requires decisions regarding their handling (4, 5). Conventional approaches include omission, resulting in a truncated data set, and imputation with a constant, such as the dl or a fraction thereof (e.g., dl/2, dl/√2); or the observed values may be used directly or indirectly (4–7). Many of these imputations have their origins in well-behaved distributions, such as normal (in the case of dl/2) and lognormal (in the case of dl/√2), and will yield correct inferences if these distributional assumptions are not grossly violated. Lubin et al. (5) propose a multiple imputation approach to handling nondetects when the exposure distribution can be assumed. Richardson and Ciampi (7) developed a coefficient of bias to linear regression coefficient estimates when exposure is measured with a detection threshold and random error, and they proposed replacement of below-threshold data by the expectation for such data (i.e., E[x|x < dl]) to yield unbiased estimates. Application of this theory to practice also requires investigators to assume an exposure distribution function. In contrast to these approaches, there has been comparatively little attention toward implicitly and explicitly nonparametric approaches to measurement with a threshold.

In this paper, the authors propose distribution-free methods for managing values below the dl and evaluate biases that result when exposure measurement is constrained by a lower threshold. Results from an analytical approach and those of a simulation study assessing the proposed replacement method are described. The proposed method allows investigators to relax the assumptions (e.g., distributional, asymptotic) necessary for use of other approaches. These results may inform decisions by investigators regarding appropriate analytical plans for future studies and provide a possible explanation for the discordance seen in current literature.

STATEMENT OF THE PROBLEM AND ANALYTICAL SOLUTION

Let the observed continuous outcome, Y, satisfy the following linear regression model:
\[Y_{i}{=}\mathrm{{\alpha}}{+}\mathrm{{\beta}}x_{i}{+}e_{i},\]
with exposure variable xi, random noise ei, and regression parameters α and β. However, x is not observed. A lower threshold, dl, interferes with measurement of low exposure levels. In a simple case, we observe z, which equals either x or “nondetects” (ND), according to the following:
\begin{eqnarray*}&&\mathrm{for}{\,}\mathrm{all}{\,}x{>}dl,{\ }z{=}x\\&&\mathrm{for}{\,}\mathrm{all}{\,}x{\leq}dl,{\ }z{=}\mathrm{ND}.\end{eqnarray*}
Alternately, when the explanatory variable is less than dl, there is quantitative random noise, ξ, rather than the qualitative response, “ND.”
In this setting, the observations are {Y1, …, Yn, z1, …, zn}. Without loss of generality, Yi and zi can be assumed to be scalars. This model can be considered in a more general context, where the exposure is measured with error, η. Thus, the linear regression model is
\[Y_{i}{=}\mathrm{{\alpha}}{+}\mathrm{{\beta}}z_{i}{+}e_{i},\]
and
\begin{eqnarray*}&&z_{i}{=}(x_{i}{+}\mathrm{{\eta}}_{i})I{\{}x_{i}{+}\mathrm{{\eta}}_{i}{\geq}dl{\}}{+}\mathrm{{\xi}}_{i}{\,}I{\{}x_{i}{+}\mathrm{{\eta}}_{i}{<}dl{\}},\\&&i{=}1,{\,}{\ldots},{\,}n\end{eqnarray*}
is the exposure with measurement error, I{•} is an indicator function (1 if {•} is true and 0 otherwise), and ei, ηi, and ξi are independent random disturbance terms related to regression error, measurement error, and detection limit error with fε(u), fη(u), and fξ(u) densities, respectively, and
\(E(e_{i}){=}0,{\,}\mathrm{var}(e_{i}){=}\mathrm{{\sigma}}_{\mathrm{{\varepsilon}}}^{2}.\)
The accuracy of regression parameter estimates depends upon the analytical approach to below-threshold values. One may consider substitution of observed z by z′, whereby
\[z{^\prime}(a){=}\left\{\begin{array}{ll}x&\mathrm{if}{\,}x{\geq}dl\\a&\mathrm{if}{\,}x{<}dl.\end{array}\right.\]

In this paper, least-squares estimation was used to determine an a that may be used in place of censored data for unbiased estimation of regression parameters. Nonnumerical and numerical instrument responses for below-threshold measurements were addressed. Additionally, the circumstances of instrument noise bounded by the detection limit (where the probability of values above the limit being due to error alone is approximately zero) and unbounded (where values above the limit will be a mix of noise alone and signal) were considered. We apply the contexts of linear regression models with both known and unknown intercepts and, additionally, provide an extension for application to logistic regression models.

Nonnumerical indicator below the detection limit

In certain situations, exposure variable values below dl are reported as “ND.” For example, this occurs when instrumentation is set to observe a threshold, and laboratory-supplied data sets include this notation for below-threshold observations. Such responses are clearly distinguished from numerical data; a decision regarding their management is required. Substitution of unobserved zi is performed according to the following equation:
\begin{eqnarray*}&&z{^\prime}_{i}{=}(x_{i}{+}\mathrm{{\eta}}_{i}){\,}I{\{}x_{i}{+}\mathrm{{\eta}}_{i}{\geq}dl{\}}{+}a{\,}I{\{}x_{i}{+}\mathrm{{\eta}}_{i}{<}dl{\}},\\&&i{=}1,{\,}{\ldots},n.\end{eqnarray*}

No intercept, α, models (condition 1A).

In cases where the intercept is known, such as reliability studies (when it is equal to zero), investigators may exclude an intercept term from models. This may also occur when modeling determinants of change from baseline or when centering data (8, 9). Even when the intercept of a general model is unknown, transformations are available to reduce its influence on estimation of other regression parameters if the intercept is not of primary interest. In each of these circumstances, the intercept may be set to a constant, and the model becomes
\[Y_{i}{-}\mathrm{{\alpha}}{=}\mathrm{{\beta}}z_{i}{+}e_{i}.\]
Without loss of generality, assume that the intercept equals zero.
Applying least-squares fitting to the unknown parameter β in the model depicted by equation 2 yields an estimator in the widely known form,
\[\mathrm{{\hat{{\beta}}}}_{n}{=}\frac{{\sum}_{i{=}1}^{n}Y_{i}z{^\prime}_{i}}{{\sum}_{i{=}1}^{n}(z{^\prime}_{i})^{2}}{=}\mathrm{{\beta}}{+}{\hat{B}}_{n}{+}E_{n},\]
where
\begin{eqnarray*}&&{\hat{B}}_{n}{=}\mathrm{{\beta}}\frac{{\sum}_{i{=}1}^{n}(x_{i}{-}z{^\prime}_{i})z{^\prime}_{i}}{{\sum}_{i{=}1}^{n}(z{^\prime}_{i})^{2}}\\&&{=}\frac{\mathrm{{\beta}}}{{\sum}_{i{=}1}^{n}(z{^\prime}_{i})^{2}}{{\sum}_{i{=}1}^{n}}({-}x_{i}\mathrm{{\eta}}_{i}I{\{}x_{i}{+}\mathrm{{\eta}}_{i}{\geq}dl{\}}\\&&{+}ax_{i}I{\{}x_{i}{+}\mathrm{{\eta}}_{i}{<}dl{\}}{-}\mathrm{{\eta}}_{i}^{2}I{\{}x_{i}{+}\mathrm{{\eta}}_{i}{\geq}dl{\}}\\&&{-}a^{2}I{\{}x_{i}{+}\mathrm{{\eta}}_{i}{<}dl{\}})\end{eqnarray*}
signifies the bias to the regression parameter, and
\[E_{n}{=}\frac{{\sum}_{i{=}1}^{n}\mathrm{{\varepsilon}}_{i}z{^\prime}_{i}}{{\sum}_{i{=}1}^{n}(z{^\prime}_{i})^{2}}\]
signifies noise with expectation zero. Assume that exposure, x, has some distribution, Fx, and is independent of e and η. Therefore, directly from equation 5, with ηi ≡ 0, there are two solutions that yield an unbiased estimator
\(\mathrm{{\hat{{\beta}}}}_{n}\)
(i.e.,
\({\hat{B}}_{\mathit{n}}\)
= 0): when a = a1 or when a = a2 (for details and solution without the restriction on ηi, refer to appendix 1):
\[a_{1}{=}\frac{{\sum}_{i{=}1}^{n}x_{i}I{\{}x_{i}{<}dl{\}}}{{\sum}_{i{=}1}^{n}I{\{}x_{i}{<}dl{\}}}\]
or
\[a_{2}{=}0.\]
Asymptotically (as n → ∞), a1 is approximately equal to E(x|x < dl) under the condition E(x2) < ∞. Replacement of values below the detection limit by this value was proposed by Richardson and Ciampi (7); however, as shown in equation 6b, the solution is not unique. There are important distinctions between these two methods; use of equation 6a assumes knowledge of the distribution function of x, whereas for a = 0, no distributional assumptions are needed.
Additionally, there are differences regarding the variance of the bias resulting from detection limit error. The variance of bias,
\(\mathrm{var}(\mathrm{{\hat{{\beta}}}}_{n}{\vert}x),\)
under a1 (equation 6a) is shown as
\begin{eqnarray*}&&\mathrm{var}(\mathrm{{\hat{{\beta}}}}_{n}{\vert}x;a_{1}){=}\mathrm{{\beta}}^{2}o_{n}(1)\\&&{+}\frac{\mathrm{{\sigma}}_{\mathrm{{\varepsilon}}}^{2}}{{\sum}_{i{=}1}^{n}(x_{i})^{2}I{\{}x_{i}{\geq}dl{\}}{+}(E(x{\vert}x{<}dl))^{2}{\sum}_{i{=}1}^{n}I{\{}x_{i}{<}dl{\}}},\end{eqnarray*}
\[{\mathrm{lim}_{n{\rightarrow}{\infty}}}{\ }{\mathrm{sup}_{\mathrm{{\beta}}}}{\ }\mathrm{var}(\mathrm{{\hat{{\beta}}}}_{n}{\vert}x;a_{1}){=}{\infty}\]
with asymptotic properties represented by the function on(1), which approaches 0 as n goes to infinity. Estimates will have some amount of bias for a fixed sample size. Conversely, under the second solution, equation 6b, the variance is derived as
\[\mathrm{var}(\mathrm{{\hat{{\beta}}}}_{n}{\vert}x;{\,}a_{2}){=}\frac{\mathrm{{\sigma}}_{\mathrm{{\varepsilon}}}^{2}}{{\sum}_{i{=}1}^{n}(x_{i})^{2}I{\{}x_{i}{\geq}dl{\}}}.\]
Note that the variance solution using a1 comprises two terms, the first being a proportion of the parameter of interest, dependent upon the sample size. The solution using a2 is invariant of the unknown parameter β; however, for “small” β, the variance may exceed that when a1 is used.

Models that estimate the intercept, α (condition 1B).

Commonly, investigators have no foreknowledge of the intercept value or a need to center their data, and the regression intercept must be estimated. As previously, consider the situation where nonnumerical noise is returned below dl. As in the previous discussion, η can be assumed to be zero, and hence the imputation is z′(a) = xI{x ≥ dl} + aI{x < dl}. Using least-squares estimation, the slope parameter estimator based on z′ instead of x can be shown as
\[\mathrm{{\beta}}_{n}{=}\frac{{{\sum}_{i{=}1}^{n}}\left(Y_{i}{-}\frac{1}{n}{\sum}_{j{=}1}^{n}Y_{j}\right)z{^\prime}_{i}}{{{\sum}_{i{=}1}^{n}}\left(z{^\prime}_{i}{-}\frac{1}{n}{\sum}_{j{=}1}^{n}z{^\prime}_{j}\right)^{2}}.\]
Again, bias results from using z′ for estimation instead of the true explanatory variables (refer to appendix 2 for equations for bias). As previously, there are two solutions for a to yield the unbiased estimator shown in equation 8. The bias is zero if and only if
\[a{=}\frac{{{\sum}_{i{=}1}^{n}}x_{i}I(x_{i}{<}dl)}{{{\sum}_{i{=}1}^{n}}I(x_{i}{<}dl)}\]
or
\[a{=}\frac{{{\sum}_{i{=}1}^{n}}x_{i}I(x_{i}{\geq}dl)}{{{\sum}_{i{=}1}^{n}}I(x_{i}{\geq}dl)}.\]
As in the previous circumstance, the Richardson and Ciampi solution (equation 9a) is valid here. Since xI[x < dl] is not observed, application of this solution requires that some distribution, Fx, be assumed for determination of the mean of the missing values. Additionally, the asymptotic result, a ≅ E(x|x < dl), as n→∞ must be assumed to be valid. However, the second solution (equation 9b) requires neither distributional nor asymptotic assumptions: The replacement value (a) may be calculated.

Numerical noise below the limit of detection

Whereas the previous sections concerned the instrumentation response of “ND,” numerical information may be available for data below dl. Importantly, if detection limit error is known to be less than the dl itself (ξ is reasonably bounded by the dl), observations below dl may be identified as such, and this becomes a special case of section 1. In this case, investigators may follow the previously discussed methodologies for models with or without intercept.

When ξ is unknown or is known to have greater magnitude than dl, the observations due to noise cannot be easily identified; the zi are observed both above and below dl for all individuals, and those with detection limit error are not easily discernible from those free of this error. Formally, suppose Pr(ξ > dl) > 0. Under the described scenario of detection limit error, this may be the case if the detection limit is set as two, rather than three (limit of detection) or 10 (limit of quantification) standard deviations of noise. In this circumstance, there is no simple approach to determining an optimal imputation; however, numerical approaches for models both with and without intercept are shown in appendix 3.

Alternatively, detection limits are occasionally determined solely on the basis of the distribution of additive random error (or concurrent detection of some contaminant). Consider true exposure, x, and all concurrently detected others, ω; all samples may be reasonably thought of as the sum of these two components (i.e., x + ω). When all levels of x are subject to the same source of error, which is independent of x, then the proposed imputations remain valid; however, alternatively, the observed values may be used for analysis in combination with commonly used methods for handling random measurement error (10, 11).

MOTIVATING EXAMPLE

We consider the association between total cholesterol and serum vitamin E in a healthy population using a population-based sample of randomly selected residents aged 35–79 years who lived in two counties in western New York State. After exclusions, a total of 857 men and women were selected for analysis. Blood specimens were analyzed for routine chemistry, hematology, and a number of chronic disease and nutritional factors, as well as serum vitamin E levels.

For cholesterol and vitamin E, all observations were measured above the dl. Regression analysis suggests a linear association between serum cholesterol and serum vitamin E (⁠

\(\mathrm{{\hat{{\beta}}}}\)
= 4.07, R2 = 0.14, p < 0.0001). However, if one stipulates that 30 percent of serum vitamin E levels are below the dl, the question arises on how to treat these “unobserved” values.

To this end, estimates were compared from linear regression of serum cholesterol on serum vitamin E. For exposure data, these models used one of the four following options: 1) all available exposure data (“gold standard”); 2) replacement of all data below the imposed threshold with the mean level of vitamin E of all data below the threshold; 3) the mean of all data above the threshold; or 4) zero. Importantly, the second circumstance relies on distributional assumptions that would be unverifiable under a true detection limit. Models were run for the known intercept as well as for estimation of the intercept.

Table 1 displays results of the known intercept regression. Replacement of subthreshold data by the average of subthreshold data yielded estimates almost identical to those when all data were used. However, under usual conditions, direct calculation of this quantity is not possible, and it must be estimated assuming some distribution. Conversely, replacement by zero requires no such assumptions and resulted in estimates not statistically different from those under the ideal scenario of no threshold. Table 2 displays results of linear regression models estimating both slope and intercept. Use of the proposed average of above-threshold data for replacement of missing data yielded good estimates of parameters, both intercept and slope. As with the use of zero for no-intercept models, use of this imputation for estimation is nonparametric and requires no distributional knowledge. Moreover, estimates of slope were hampered by slight departures from the assumptions of linear regression of the data. Use of zero for replacement of missing data resulted in estimates statistically different from those under no constraint by a detection threshold.

TABLE 1.

Coefficient estimates from linear regression with a known intercept of serum cholesterol on serum vitamin E, with values below the limit of detection replaced by the average (x|x < dl*) and zero

All values (reference)
Replace by average (x|x < dl)
Replace by zero
\(\mathrm{{\hat{{\beta}}}}\)
4.074.064.19
SE*
\((\mathrm{{\hat{{\beta}}}})\)
0.140.140.15
95% CI*
\((\mathrm{{\hat{{\beta}}}})\)
3.80, 4.34
3.79, 4.33
3.90, 4.48
All values (reference)
Replace by average (x|x < dl)
Replace by zero
\(\mathrm{{\hat{{\beta}}}}\)
4.074.064.19
SE*
\((\mathrm{{\hat{{\beta}}}})\)
0.140.140.15
95% CI*
\((\mathrm{{\hat{{\beta}}}})\)
3.80, 4.34
3.79, 4.33
3.90, 4.48
*

dl, detection limit; SE, standard error; CI, confidence interval.

Open in new tab
TABLE 1.

Coefficient estimates from linear regression with a known intercept of serum cholesterol on serum vitamin E, with values below the limit of detection replaced by the average (x|x < dl*) and zero

All values (reference)
Replace by average (x|x < dl)
Replace by zero
\(\mathrm{{\hat{{\beta}}}}\)
4.074.064.19
SE*
\((\mathrm{{\hat{{\beta}}}})\)
0.140.140.15
95% CI*
\((\mathrm{{\hat{{\beta}}}})\)
3.80, 4.34
3.79, 4.33
3.90, 4.48
All values (reference)
Replace by average (x|x < dl)
Replace by zero
\(\mathrm{{\hat{{\beta}}}}\)
4.074.064.19
SE*
\((\mathrm{{\hat{{\beta}}}})\)
0.140.140.15
95% CI*
\((\mathrm{{\hat{{\beta}}}})\)
3.80, 4.34
3.79, 4.33
3.90, 4.48
*

dl, detection limit; SE, standard error; CI, confidence interval.

Open in new tab
TABLE 2.

Coefficient estimates from linear regression of serum cholesterol on serum vitamin E, with values below the limit of detection replaced by the average (x|x < dl*), average (x|x > dl), and zero

All values (reference)
Replace by average (x|x < dl)
Replace by average (x|x > dl)
Replace by zero
\(\mathrm{{\hat{{\alpha}}}}\)
196.88197.39204.53219.76
SE*
\((\mathrm{{\hat{{\alpha}}}})\)
5.215.267.513.35
95% CI*
\((\mathrm{{\hat{{\alpha}}}})\)
186.67, 207.09187.08, 207.7189.81, 219.25213.19, 226.33
\(\mathrm{{\hat{{\beta}}}}\)
4.074.033.022.89
SE
\((\mathrm{{\hat{{\beta}}}})\)
0.360.360.460.24
95% CI
\((\mathrm{{\hat{{\beta}}}})\)
3.36, 4.78
3.32, 4.74
2.12, 3.92
2.42, 3.36
All values (reference)
Replace by average (x|x < dl)
Replace by average (x|x > dl)
Replace by zero
\(\mathrm{{\hat{{\alpha}}}}\)
196.88197.39204.53219.76
SE*
\((\mathrm{{\hat{{\alpha}}}})\)
5.215.267.513.35
95% CI*
\((\mathrm{{\hat{{\alpha}}}})\)
186.67, 207.09187.08, 207.7189.81, 219.25213.19, 226.33
\(\mathrm{{\hat{{\beta}}}}\)
4.074.033.022.89
SE
\((\mathrm{{\hat{{\beta}}}})\)
0.360.360.460.24
95% CI
\((\mathrm{{\hat{{\beta}}}})\)
3.36, 4.78
3.32, 4.74
2.12, 3.92
2.42, 3.36
*

dl, detection limit; SE, standard error; CI, confidence interval.

Open in new tab
TABLE 2.

Coefficient estimates from linear regression of serum cholesterol on serum vitamin E, with values below the limit of detection replaced by the average (x|x < dl*), average (x|x > dl), and zero

All values (reference)
Replace by average (x|x < dl)
Replace by average (x|x > dl)
Replace by zero
\(\mathrm{{\hat{{\alpha}}}}\)
196.88197.39204.53219.76
SE*
\((\mathrm{{\hat{{\alpha}}}})\)
5.215.267.513.35
95% CI*
\((\mathrm{{\hat{{\alpha}}}})\)
186.67, 207.09187.08, 207.7189.81, 219.25213.19, 226.33
\(\mathrm{{\hat{{\beta}}}}\)
4.074.033.022.89
SE
\((\mathrm{{\hat{{\beta}}}})\)
0.360.360.460.24
95% CI
\((\mathrm{{\hat{{\beta}}}})\)
3.36, 4.78
3.32, 4.74
2.12, 3.92
2.42, 3.36
All values (reference)
Replace by average (x|x < dl)
Replace by average (x|x > dl)
Replace by zero
\(\mathrm{{\hat{{\alpha}}}}\)
196.88197.39204.53219.76
SE*
\((\mathrm{{\hat{{\alpha}}}})\)
5.215.267.513.35
95% CI*
\((\mathrm{{\hat{{\alpha}}}})\)
186.67, 207.09187.08, 207.7189.81, 219.25213.19, 226.33
\(\mathrm{{\hat{{\beta}}}}\)
4.074.033.022.89
SE
\((\mathrm{{\hat{{\beta}}}})\)
0.360.360.460.24
95% CI
\((\mathrm{{\hat{{\beta}}}})\)
3.36, 4.78
3.32, 4.74
2.12, 3.92
2.42, 3.36
*

dl, detection limit; SE, standard error; CI, confidence interval.

Open in new tab

LOGISTIC REGRESSION

Frequently, investigators face exposure measurement thresholds when investigating binary outcomes (e.g., presence or absence of disease) using logistic regression models for evaluation of risk. These models are often used for analysis of case-control study data. In this context, investigators rarely have an interest in intercept estimates, interpretation of which is generally meaningless (9). In such situations, the discussion for condition 1A is applicable, and bias is minimized when a equals zero. This is shown empirically in a simulation study described in the next section. A more detailed discussion and proof are shown in appendices 4 and 5.

The solution under maximum likelihood estimation is complicated, even with known intercept. When the intercept is unknown, solutions to two nonlinear equations are required (appendix 5). A solution can be determined only in rare cases and where strong assumptions regarding the observed data are used and where the proposed methodology is applied. However, this problem is beyond the scope of this paper.

MONTE CARLO SIMULATION STUDY

We extend previous work (7) to apply a solution to the detection limit problem to binary disease variables and to use of a logit-linear model. To evaluate the effects of detection limit bias on logistic regression, 10,000 data sets were simulated, with n = 300, outcome = Y, and measured exposure z to comprise the observations {(Yi, zi(a)), i = 1, …, n}, following the model,
\[P{\{}Y_{i}{=}1{\vert}x_{i}{\}}{=}(1{+}\mathrm{exp}({-}c{-}\mathrm{{\beta}}x_{i}))^{{-}1},\]
\[z_{i}(a){=}x_{i}{\,}I{\{}x_{i}{\geq}dl{\}}{+}a{\,}I{\{}x_{i}{<}dl{\}}.\]
We evaluated two distributions for the exposure of interest. A bimodal distribution was chosen to exemplify a poorly behaved density, and a gamma distribution (a skewed distribution often assumed for biomarkers) was also evaluated (figure 1). After data for the true exposure were generated, several detection thresholds were applied. The observed exposure was determined after replacement of values below the detection limit for both a1{a = E(x|x < dl)} and a2{a = 0} according to the above, as well as for the common imputations a = dl and a = dl/2. Bias and variance were assessed by comparing results based on use of true exposure with those subject to detection limits.
FIGURE 1.
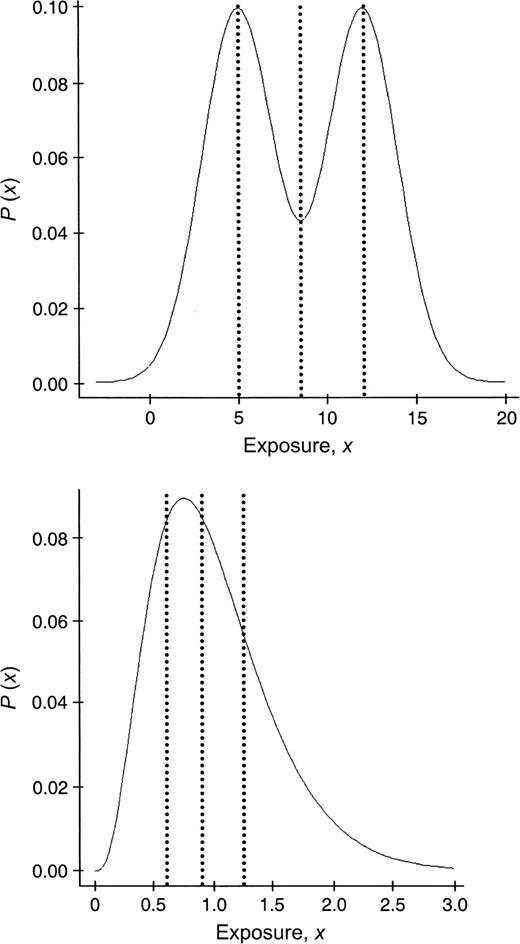
Probability distribution functions for Monte Carlo simulation study: exposure-distributed bimodal normal (top) and gamma (bottom). Dotted lines indicate the values utilized for the threshold corresponding to the 25th, 50th, and 75th percentiles.
Open in new tabDownload slide

Probability distribution functions for Monte Carlo simulation study: exposure-distributed bimodal normal (top) and gamma (bottom). Dotted lines indicate the values utilized for the threshold corresponding to the 25th, 50th, and 75th percentiles.

Table 3 displays the simulated Monte Carlo variance of the maximum likelihood estimator

\(\mathrm{{\hat{{\beta}}}},{\,}\mathrm{var}(a){=}\overline{(\mathrm{{\beta}}{-}\mathrm{{\hat{{\beta}}}})^{2}},\)
and the Monte Carlo average bias,
\(\mathrm{bias}(a){=}\overline{\mathrm{{\beta}}{-}\mathrm{{\hat{{\beta}}}}},\)
for each evaluated a under the bimodal distribution for exposure. The specified values for dl correspond to the circumstances where 25 percent, 50 percent, and 75 percent of data are below the threshold. In most cases, imputation of zero resulted in minimally biased estimates, with Monte Carlo relative biases comparable with those observed under use of the E(x|x < dl). Imputation of dl and dl/2 resulted in substantially greater biases. Table 4 displays the results of simulations where exposure is gamma distributed. Results for the gamma-distributed exposure were similar to those for the bimodal distribution; imputation of zero and E(x|x < dl) performed similarly well, while use of dl or dl/2 resulted in substantially biased estimates.

TABLE 3.

Logistic regression simulation study with bimodal normal distributed exposure: bias and variance of the estimator under replacement value, a, equal to zero, E(x|x < dl*), dl, and dl/2†

β
d
x < dl (%)
Bias (Monte Carlo estimator of β)
Variance (Monte Carlo estimator of β)
a =
a =
0
E(x|x < d)
dl
dl/2
0
E(x|x < d)
dl
dl/2
0.35250.000260.000190.001170.000570.000250.000250.000270.00026
8.5500.000680.000590.01407−0.000820.000260.000250.000430.00026
12750.00117−0.007960.053600.001970.000390.000380.003070.00046
0.5525−0.00045−0.000750.00276−0.001270.000240.000240.000240.00024
8.550−0.00062−0.005180.04611−0.008330.000280.000310.002250.00037
1275−0.00183−0.044090.12608−0.083980.000680.002390.015980.00794
0.7525−0.00230−0.004760.01814−0.008070.000680.000680.000780.00077
8.5500.00668−0.038780.14702−0.091310.001600.002530.021740.02174
12
75
−0.12120
−0.07991
0.26264
0.14123
0.10959
0.07712
0.16906
0.14076
β
d
x < dl (%)
Bias (Monte Carlo estimator of β)
Variance (Monte Carlo estimator of β)
a =
a =
0
E(x|x < d)
dl
dl/2
0
E(x|x < d)
dl
dl/2
0.35250.000260.000190.001170.000570.000250.000250.000270.00026
8.5500.000680.000590.01407−0.000820.000260.000250.000430.00026
12750.00117−0.007960.053600.001970.000390.000380.003070.00046
0.5525−0.00045−0.000750.00276−0.001270.000240.000240.000240.00024
8.550−0.00062−0.005180.04611−0.008330.000280.000310.002250.00037
1275−0.00183−0.044090.12608−0.083980.000680.002390.015980.00794
0.7525−0.00230−0.004760.01814−0.008070.000680.000680.000780.00077
8.5500.00668−0.038780.14702−0.091310.001600.002530.021740.02174
12
75
−0.12120
−0.07991
0.26264
0.14123
0.10959
0.07712
0.16906
0.14076
*

dl, detection limit.

†

Values of E(x|x < d) are as follows: 3.405 for d = 5; 4.934 for d = 8.5; 6.700 for d = 12. P{Yi = 1|xi} = (1 + exp(−c − βxi))−1, where c = −5, c is known, and xi = N(5, 22)(1−θi) + N(12, 22)θi, where θi, i ≥ 1 are independent, identically Bernoulli-distributed random variables with P{θi = 1} = 1/2.

Open in new tab
TABLE 3.

Logistic regression simulation study with bimodal normal distributed exposure: bias and variance of the estimator under replacement value, a, equal to zero, E(x|x < dl*), dl, and dl/2†

β
d
x < dl (%)
Bias (Monte Carlo estimator of β)
Variance (Monte Carlo estimator of β)
a =
a =
0
E(x|x < d)
dl
dl/2
0
E(x|x < d)
dl
dl/2
0.35250.000260.000190.001170.000570.000250.000250.000270.00026
8.5500.000680.000590.01407−0.000820.000260.000250.000430.00026
12750.00117−0.007960.053600.001970.000390.000380.003070.00046
0.5525−0.00045−0.000750.00276−0.001270.000240.000240.000240.00024
8.550−0.00062−0.005180.04611−0.008330.000280.000310.002250.00037
1275−0.00183−0.044090.12608−0.083980.000680.002390.015980.00794
0.7525−0.00230−0.004760.01814−0.008070.000680.000680.000780.00077
8.5500.00668−0.038780.14702−0.091310.001600.002530.021740.02174
12
75
−0.12120
−0.07991
0.26264
0.14123
0.10959
0.07712
0.16906
0.14076
β
d
x < dl (%)
Bias (Monte Carlo estimator of β)
Variance (Monte Carlo estimator of β)
a =
a =
0
E(x|x < d)
dl
dl/2
0
E(x|x < d)
dl
dl/2
0.35250.000260.000190.001170.000570.000250.000250.000270.00026
8.5500.000680.000590.01407−0.000820.000260.000250.000430.00026
12750.00117−0.007960.053600.001970.000390.000380.003070.00046
0.5525−0.00045−0.000750.00276−0.001270.000240.000240.000240.00024
8.550−0.00062−0.005180.04611−0.008330.000280.000310.002250.00037
1275−0.00183−0.044090.12608−0.083980.000680.002390.015980.00794
0.7525−0.00230−0.004760.01814−0.008070.000680.000680.000780.00077
8.5500.00668−0.038780.14702−0.091310.001600.002530.021740.02174
12
75
−0.12120
−0.07991
0.26264
0.14123
0.10959
0.07712
0.16906
0.14076
*

dl, detection limit.

†

Values of E(x|x < d) are as follows: 3.405 for d = 5; 4.934 for d = 8.5; 6.700 for d = 12. P{Yi = 1|xi} = (1 + exp(−c − βxi))−1, where c = −5, c is known, and xi = N(5, 22)(1−θi) + N(12, 22)θi, where θi, i ≥ 1 are independent, identically Bernoulli-distributed random variables with P{θi = 1} = 1/2.

Open in new tab
TABLE 4.

Logistic regression simulation study with gamma distributed exposure: bias and variance of the estimator under replacement value, a, equal to zero, E(x|x < dl*), dl, and dl/2†

β
d
x < dl (%)
Bias (Monte Carlo estimator of β)
Variance (Monte Carlo estimator of β)
a =
a =
0
E(x|x < d)
dl
dl/2
0
E(x|x < d)
dl
dl/2
0.30.634250.001530.001480.00730−0.001650.012040.011480.014120.01373
0.919500.003090.002800.02926−0.005950.013730.012690.015800.01450
1.278750.007080.005860.07383−0.013680.013840.012890.016280.01474
1.50.63425−0.00427−0.004050.04319−0.023750.016360.015820.016990.01732
0.91950−0.00630−0.005990.18292−0.079870.019330.015900.044080.02821
1.278
75
−0.01079
0.00085
0.42685
−0.14473
0.02450
0.01982
0.18934
0.04348
β
d
x < dl (%)
Bias (Monte Carlo estimator of β)
Variance (Monte Carlo estimator of β)
a =
a =
0
E(x|x < d)
dl
dl/2
0
E(x|x < d)
dl
dl/2
0.30.634250.001530.001480.00730−0.001650.012040.011480.014120.01373
0.919500.003090.002800.02926−0.005950.013730.012690.015800.01450
1.278750.007080.005860.07383−0.013680.013840.012890.016280.01474
1.50.63425−0.00427−0.004050.04319−0.023750.016360.015820.016990.01732
0.91950−0.00630−0.005990.18292−0.079870.019330.015900.044080.02821
1.278
75
−0.01079
0.00085
0.42685
−0.14473
0.02450
0.01982
0.18934
0.04348
*

dl, detection limit.

†

Values of E(x|x < d) are as follows: 0.454 for d = 0.634; 0.615 for d = 0.919; 0.772 for d = 1.278. P{Yi = 1|xi} = (1 + exp(−c − βxi))−1, where c = −1, c is known, and xi ∼ gamma(shape = 4, scale = 4).

Open in new tab
TABLE 4.

Logistic regression simulation study with gamma distributed exposure: bias and variance of the estimator under replacement value, a, equal to zero, E(x|x < dl*), dl, and dl/2†

β
d
x < dl (%)
Bias (Monte Carlo estimator of β)
Variance (Monte Carlo estimator of β)
a =
a =
0
E(x|x < d)
dl
dl/2
0
E(x|x < d)
dl
dl/2
0.30.634250.001530.001480.00730−0.001650.012040.011480.014120.01373
0.919500.003090.002800.02926−0.005950.013730.012690.015800.01450
1.278750.007080.005860.07383−0.013680.013840.012890.016280.01474
1.50.63425−0.00427−0.004050.04319−0.023750.016360.015820.016990.01732
0.91950−0.00630−0.005990.18292−0.079870.019330.015900.044080.02821
1.278
75
−0.01079
0.00085
0.42685
−0.14473
0.02450
0.01982
0.18934
0.04348
β
d
x < dl (%)
Bias (Monte Carlo estimator of β)
Variance (Monte Carlo estimator of β)
a =
a =
0
E(x|x < d)
dl
dl/2
0
E(x|x < d)
dl
dl/2
0.30.634250.001530.001480.00730−0.001650.012040.011480.014120.01373
0.919500.003090.002800.02926−0.005950.013730.012690.015800.01450
1.278750.007080.005860.07383−0.013680.013840.012890.016280.01474
1.50.63425−0.00427−0.004050.04319−0.023750.016360.015820.016990.01732
0.91950−0.00630−0.005990.18292−0.079870.019330.015900.044080.02821
1.278
75
−0.01079
0.00085
0.42685
−0.14473
0.02450
0.01982
0.18934
0.04348
*

dl, detection limit.

†

Values of E(x|x < d) are as follows: 0.454 for d = 0.634; 0.615 for d = 0.919; 0.772 for d = 1.278. P{Yi = 1|xi} = (1 + exp(−c − βxi))−1, where c = −1, c is known, and xi ∼ gamma(shape = 4, scale = 4).

Open in new tab

DISCUSSION

We have considered analysis of exposures subject to a lower threshold, a circumstance frequently confronted in epidemiologic studies evaluating relations between laboratory data and health outcomes. Appropriate management of data below such a threshold is imperative for proper conclusions, and available information may not be sufficient for use of parametric approaches. By use of an analytical approach to finding unbiased estimators, substitution of zero for subthreshold/missing data was observed to minimize bias when using no/known intercept linear regression models; when estimating the intercept, imputation of the average of data above detection limits yielded optimal estimates. Data from a population-based study were used to display the effects of the proposed solutions. Additionally, Monte Carlo simulations were used to demonstrate solutions applied to logistic regression where the intercept is known and/or excluded from models, which is appropriate for case-control study data. Imputation of zero performed optimally in these circumstances.

While this result may seem illogical, the solutions for linear regression may be understood intuitively. Imputation of zero for exposure values below detection limits essentially eliminates the leverage of those data on estimation when concerned solely with the slope of the regression line (i.e., the no-intercept model). If the data perfectly meet the assumptions for this model, then use of the subset of data above the threshold will yield estimates identical to those produced using all the data when they are not subject to a threshold. Similarly, imputation of the expected value for all observed data (i.e., z > dl) eliminates the leverage of those data points on estimation of the regression line slope while also allowing for estimation of the intercept; imputation of zero clearly has implications for estimation of the linear regression intercept.

The real data example results display the effectiveness of these imputations as well as certain limitations. Estimates under the proposed imputations were not statistically different from those subjected to no detection threshold nor were they identical. In combination with normal sampling variability, when data do not perfectly conform to the assumptions for linear regression, this is expected to be the case. Nonlinear relations can be poorly represented when a subset of data is observable. Additionally, when error is not normally and/or identically distributed, data with disproportionate leverage on estimation may be subject to the threshold, and the parameter estimates may be unequal to those without a detection threshold. Importantly, in these cases, the estimates under a no-threshold linear model are subject to the same limitations; data transformation techniques should be considered. Under the assumptions of linear regression, imputation of zero for no intercept or of the mean of observed values for intercept models is appropriate for investigators opting for nonparametric approaches.

Various approaches to management of data measured with a lower limit including imputations derived from the limit of detection itself, such as dl/2 or dl/√2, have been used in laboratory and data analysis settings (4, 6, 12). A multiple imputation approach based on bootstrapping has also been proposed (5). The utility of these approaches depends upon proper determination of the exposure distribution function. Recent work showed that use of E(x|x < dl) for those data below detection limits allows unbiased estimation of linear and, under certain conditions, logistic regression parameters; however, this approach requires assumptions regarding the underlying exposure distribution. We have shown that unbiased estimates may also be obtained if data below the detection limit are replaced by zero for no-intercept models and by E(x|x > dl) for models estimating the intercept; use of these methods requires no distributional assumptions.

We performed Monte Carlo simulations of bimodal and gamma exposures with a logit-linear relation to the outcome and stipulated varying proportions of the data to be below a detection threshold. Under a no-intercept model (α = 0) with slope parameter equal to 0.3 (odds ratio = 1.35), imputation of zero resulted in similarly minimally biased results as use of E(x|x < dl). This approach may be useful for logistic regression models when available information makes distributional assumptions difficult to validate, thereby extending upon previously published work (7). We have presented analytical solutions for linear regression and no-intercept logistic regression; the solutions presented here are not generalizable to other complex modeling situations.

CONCLUSION

Measurement of laboratory data can be limited by a detection threshold when sample exposure levels are in the range of that threshold. When a meaningful proportion of data falls below the detection threshold, there is a need for simple yet valid approaches to handling the data. When investigators are confident of the validity of distributional assumptions, parametric methods may be used. We have demonstrated approaches that require no distributional assumptions and are easily applied to achieve unbiased estimates. In all cases, sensitivity analyses to evaluate the chosen approach are recommended. Importantly, this paper has focused on analytical studies primarily interested in estimating linear relations between signal and response. Nevertheless, investigators should evaluate the nature of the data, the detection limit, and the parameter to be estimated when choosing the optimal method for management of subthreshold data.

APPENDIX 1

Application of the definition for z′ from equation 3,
\[z{^\prime}_{i}{=}(x_{i}{+}\mathrm{{\eta}}_{i}){\,}I{\{}x_{i}{+}\mathrm{{\eta}}_{i}{\geq}d{\}}{+}a{\,}I{\{}x_{i}{+}\mathrm{{\eta}}_{i}{<}d{\}},{\ }i{=}1,{\,}{\ldots},n,\]
to equation 5 for the least-squares estimator with detection limit error,
\[{\hat{B}}_{n}{=}\mathrm{{\beta}}\frac{{\sum}_{i{=}1}^{n}(x_{i}{-}z{^\prime}_{i})z{^\prime}_{i}}{{\sum}_{i{=}1}^{n}(z{^\prime}_{i})^{2}},\]
yields the following:
\[{=}\frac{\mathrm{{\beta}}}{{\sum}_{i{=}1}^{n}(z{^\prime}_{i})^{2}}{{\sum}_{i{=}1}^{n}}({-}x_{i}\mathrm{{\eta}}_{i}I{\{}x_{i}{+}\mathrm{{\eta}}_{i}{\geq}d{\}}{+}ax_{i}I{\{}x_{i}{+}\mathrm{{\eta}}_{i}{<}d{\}}{-}\mathrm{{\eta}}_{i}^{2}I{\{}x_{i}{+}\mathrm{{\eta}}_{i}{\geq}d{\}}{-}a^{2}I{\{}x_{i}{+}\mathrm{{\eta}}_{i}{<}d{\}}).\]
The bias of estimator
\(\mathrm{{\hat{{\beta}}}}_{n}\)
is zero (i.e.,
\({\hat{B}}_{n}\)
= 0) if and only if the numerator of
\({\hat{B}}_{n}\)
(equation 5) is equal to zero:
\[a^{2}\frac{1}{n}{{\sum}_{i{=}1}^{n}}I{\{}x_{i}{+}\mathrm{{\eta}}_{i}{<}d{\}}{-}a\frac{1}{n}{{\sum}_{i{=}1}^{n}}x_{i}I{\{}x_{i}{+}\mathrm{{\eta}}_{i}{<}d{\}}{+}\frac{1}{n}{{\sum}_{i{=}1}^{n}}(\mathrm{{\eta}}_{i}^{2}I{\{}x_{i}{+}\mathrm{{\eta}}_{i}{\geq}d{\}}{+}x_{i}\mathrm{{\eta}}_{i}I{\{}x_{i}{+}\mathrm{{\eta}}_{i}{\geq}d{\}}){=}0.\]
Asymptotically (as n → ∞), under the restrictions 1) E(x2) < ∞, 2) E(|ξ|)3 < ∞, and 3) E(xξ)2 < ∞, the solution of equation 5 is almost surely equal to the solution of
\[a^{2}\mathrm{Pr}{\{}x_{1}{+}\mathrm{{\eta}}_{1}{<}d{\}}{-}a{\,}E(x_{1},x_{1}{+}\mathrm{{\eta}}_{1}{<}d){+}E(\mathrm{{\eta}}_{1}^{2},x_{1}{+}\mathrm{{\eta}}_{1}{\geq}d){+}E(x_{1}\mathrm{{\eta}}_{1},x_{1}{+}\mathrm{{\eta}}_{1}{\geq}d){=}0.\]
The preceding determines an “a” such that bias,
\({\hat{B}}_{n},\)
equals zero, asymptotically. When detection limit error can be clearly delineated, that is, Pr(ξ < d) ≡ 1, a may be either a1 = E(x|x < d) or a2 = 0.

APPENDIX 2

For estimation of the regression parameter and unknown intercept when exposure is measured with a threshold,
\[{\hat{B}}_{n}{=}\mathrm{{\beta}}\frac{{{\sum}_{i{=}1}^{n}}z{^\prime}_{i}\left(x_{i}{-}\frac{1}{n}{\sum}_{j{=}1}^{n}x_{i}\right){-}{{\sum}_{i{=}1}^{n}}\left(z{^\prime}_{i}{-}\frac{1}{n}{\sum}_{j{=}1}^{n}z{^\prime}_{j}\right)^{2}}{{{\sum}_{i{=}1}^{n}}\left(z{^\prime}_{i}{-}\frac{1}{n}{\sum}_{j{=}1}^{n}z{^\prime}_{j}\right)^{2}}.\]
The numerator of
\({\hat{B}}_{n}\)
may be demonstrated as
\begin{eqnarray*}&&{{\sum}_{i{=}1}^{n}}z{^\prime}_{i}\left(x_{i}{-}\frac{1}{n}{\sum}_{j{=}1}^{n}x_{i}\right){-}{{\sum}_{i{=}1}^{n}}\left(z{^\prime}_{i}{-}\frac{1}{n}{\sum}_{j{=}1}^{n}z{^\prime}_{j}\right)^{2}\\&&{=}{{\sum}_{i{=}1}^{n}}x_{i}^{2}I(x_{i}{\geq}dl){+}a{{\sum}_{i{=}1}^{n}}x_{i}I(x_{i}{<}dl){-}\frac{1}{n}{{\sum}_{i{=}1}^{n}}x_{i}{{\sum}_{i{=}1}^{n}}x_{i}I(x_{i}{\geq}dl){-}\frac{a}{n}{{\sum}_{i{=}1}^{n}}x_{i}{{\sum}_{i{=}1}^{n}}I(x_{i}{<}dl){-}{{\sum}_{i{=}1}^{n}}x_{i}^{2}I(x_{i}{\geq}dl)\\&&{-}a^{2}{{\sum}_{i{=}1}^{n}}I(x_{i}{<}dl){+}\frac{1}{n}\left({{\sum}_{i{=}1}^{n}}x_{i}I(x_{i}{\geq}dl)\right)^{2}{+}\frac{2a}{n}{{\sum}_{i{=}1}^{n}}x_{i}I(x_{i}{\geq}dl){{\sum}_{i{=}1}^{n}}I(x_{i}{<}dl){+}\frac{a^{2}}{n}\left({{\sum}_{i{=}1}^{n}}I(x_{i}{\geq}dl)\right)^{2}\\&&{=}{-}\left[a{{\sum}_{i{=}1}^{n}}I(x_{i}{<}dl){-}{{\sum}_{i{=}1}^{n}}x_{i}I(x_{i}{<}dl)\right]\left[\frac{a}{n}{{\sum}_{i{=}1}^{n}}I(x_{i}{\geq}dl){-}\frac{1}{n}{{\sum}_{i{=}1}^{n}}x_{i}I(x_{i}{\geq}dl)\right].\end{eqnarray*}
Hence, the bias is equal to zero if the right side of equation A2.1 is equal to zero.

APPENDIX 3

For models not estimating the intercept with a numerical response below dl rather than “ND,” first define a substitution of observed z,
\[z{^\prime}_{i}(a){=}z_{i}{\,}I{\{}z_{i}{\geq}dl{^\prime}{\}}{+}a{\,}I{\{}z_{i}{<}dl{^\prime}{\}},{\ }\mathrm{for}{\,}i{=}1,{\,}{\ldots},{\,}n,\]
where dl′ is the fixed detection limit. The bias of the least-squares estimator is given by
\[{\hat{B}}_{n}{=}\mathrm{{\beta}}\frac{{\sum}_{i{=}1}^{n}(x_{i}{-}z{^\prime}_{i})z{^\prime}_{i}}{{\sum}_{i{=}1}^{n}(z{^\prime}_{i})^{2}}.\]
In this case, bias
\({\hat{B}}_{n}\)
is asymptotically close to zero if a and d′ are solutions of the equation,
\[E(z{^\prime}_{1}x_{1}){-}E(z{^\prime}_{1})^{2}{=}0.\]

Solving equation A3.3 requires that the distribution functions of xi, ηi, and ξ be assumed, which may be performed numerically by grid searching a and dl′ such that the left side of equation A3.3 is approximately equal to zero.

When the density function of regression error is known and well behaved, then we may consider maximum likelihood estimation of β,
\[\mathrm{{\hat{{\beta}}}}_{n}{=}\mathrm{arg}{\ }{\mathrm{max}_{b}}{{\prod}_{i{=}1}^{n}}f_{\mathrm{{\varepsilon}}}(Y_{i}{-}bz{^\prime}_{i}),\]
and the consideration of bias reduction from conditions 1A and 1B is similarly relevant here.
To address a numerical response below dl when estimating the intercept, we use the replacement defined in appendix equation A3.1. Using the proposed method, in the case where the distributions of all random variables in equation 1 are known, we obtain the unbiased least-square estimator of parameter β based upon the sample {Y, z′} by applying a and d′ such that
\[E[z{^\prime}(x{-}E(x)]{-}E[z{^\prime}{-}E(z{^\prime})]^{2}{=}0.\]

APPENDIX 4

Note that, asymptotically, by the definition of least-squares slope parameter estimators under the detection limit problem (e.g., equation A1.2), we attain

\(E\mathrm{{\hat{{\beta}}}}_{n}{\rightarrow}\mathrm{{\lambda}{\beta}},\)
where
\(\mathrm{{\lambda}}{=}\frac{\mathrm{cov}(x,{\,}z{^\prime})}{\mathrm{var}(z{^\prime})}.\)
This form is similar to an asymptotic property of the ordinary least-squares estimator of the parameters from linear regression with additive measurement error (7).

APPENDIX 5

The logistic regression model with exposure measurement error is given by
\[P(Y_{i}{=}1{\vert}x_{i}){=}(1{+}e^{{-}\mathrm{{\beta}}z_{i}})^{{-}1},\]
\[z_{i}{=}(x_{i}{+}\mathrm{{\eta}}_{i})I{\{}x_{i}{+}\mathrm{{\eta}}_{i}{\geq}d{\}}{+}\mathrm{{\xi}}_{i}{\,}I{\{}x_{i}{+}\mathrm{{\eta}}_{i}{<}d{\}},{\ }i{=}1,{\,}{\ldots},{\,}n,\]
where Yi, i = 1, …, n are Bernoulli variates whose exact distribution depends on the predictor xi. Let xi + ηi be observed if xi + ηi ≥ d ; hence, we assume a substitution of observed zi by
\(z{^\prime}_{i}{=}(x_{i}{+}\mathrm{{\eta}}_{i}){\,}I{\{}x_{i}{+}\mathrm{{\eta}}_{i}{\geq}d{\}}{+}a{\,}I{\{}x_{i}{+}\mathrm{{\eta}}_{i}{<}d{\}},{\,}i{=}1,{\ldots},n.\)
Applying the maximum likelihood method, we obtain the estimator of β by solving the following:
\[{{\sum}_{i{=}1}^{n}}z{^\prime}_{i}\left(Y_{i}{-}\frac{e^{\mathrm{{\hat{{\beta}}}}_{n}z{^\prime}_{i}}}{1{+}e^{{\hat{{\beta}}}_{n}z{^\prime}_{i}}}\right){=}0.\]
It follows from the usual Taylor expansion that
\[\mathrm{{\hat{{\beta}}}}_{n}{-}\mathrm{{\beta}}{=}\left[{{\sum}_{i{=}1}^{n}}z{^\prime}_{i}\left(Y_{i}{-}\frac{e^{\mathrm{{\beta}}x_{i}}}{1{+}e^{\mathrm{{\beta}}x_{i}}}\right){+}\mathrm{{\beta}}{{\sum}_{i{=}1}^{n}}z{^\prime}_{i}(x_{i}{-}z{^\prime}_{i})Q_{i}\right]\left[{{\sum}_{i{=}1}^{n}}(z{^\prime}_{i})^{2}{\,}Qi\right]^{{-}1},\]
\[Q_{i}{\in}\left(\frac{e^{\mathrm{{\beta}}x_{i}}}{(1{+}e^{\mathrm{{\beta}}x_{i}})^{2}},\frac{e^{{\hat{{\beta}}}_{n}z{^\prime}_{i}}}{(1{+}e^{{\hat{{\beta}}}_{n}z{^\prime}_{i}})^{2}}\right).\]
Thus, in this case, the detection limit error bias is defined by
\[{\hat{B}}_{n}{=}\frac{\mathrm{{\beta}}{\sum}_{i{=}1}^{n}z{^\prime}_{i}(x_{i}{-}z{^\prime}_{i}){\,}Q_{i}}{{{\sum}_{i{=}1}^{n}}(z{^\prime}_{i})^{2}{\,}Q_{i}}.\]
Therefore, even though ηi = 0, i = 1, …, n, we obtain
\[{\hat{B}}_{n}{=}\frac{\mathrm{{\beta}}{\sum}_{i{=}1}^{n}(ax_{i}I(x_{i}{<}d){-}a^{2}I(x_{i}{<}d)){\,}Q_{i}}{{{\sum}_{i{=}1}^{n}}(z{^\prime}_{i})^{2}{\,}Q_{i}},\]
where
\({\hat{B}}\)
n is zero only if a is zero, because generally Qi is dependent on i, target unknown β, and unobserved xi.

This research was supported by the Intramural Research Program of the National Institutes of Health (Epidemiology Branch, Division of Epidemiology, Statistics, and Prevention Research, National Institute of Child Health and Human Development).

The authors thank Dr. Maurizio Trevisan for providing access to the MI Life Study data set.

Conflict of interest: none declared.

References

1.

Cooper GS, Savitz DA, Millikan R, et al. Organochlorine exposure and age at natural menopause.

Epidemiology
2002
;
13
:
729
–33.

2.

Karaszkiewicz JW. Critical factors in immunoassay optimization. Gaithersburg, MD: Kirkegaard & Perry Laboratories, Inc,

2005
. (http://www.kpl.com/docs/techdocs/BENCH2.PDF). Accessed July 1, 2005.

3.

Keith LH, Crummett W, Deegan J, et al. Principles of environmental analysis.

Anal Chem
1983
;
55
:
2210
–18.

4.

Helsel D. Nondetects and data analysis: statistics for censored environmental data. Hoboken, NJ: John Wiley & Sons, Inc,

2005
.

5.

Lubin JH, Colt JS, Camann D, et al. Epidemiologic evaluation of measurement data in the presence of detection limits.

Environ Health Perspect
2004
;
112
:
1691
–6.

6.

Hornung RW, Reed LD. Estimation of average concentration in the presence of nondetectable values.

Appl Occup Environ Hyg
1990
;
5
:
46
–51.

7.

Richardson DB, Ciampi A. Effects of exposure measurement error when an exposure variable is constrained by a lower limit.

Am J Epidemiol
2003
;
157
:
355
–63.

8.

Draper NR, Smith H. Applied regression analysis. New York, NY: John Wiley & Sons, Inc,

1998
.

9.

Greenland S. Introduction to regression modeling. In: Rothman KJ, Greenland S, eds. Modern epidemiology. 2nd ed. Philadelphia, PA: Lippincott Williams & Wilkins,

1998
:401–32.

10.

Rosner B, Willett WC, Spiegelman D. Correction of logistic regression relative risk estimates and confidence intervals for systematic within-person measurement error.

Stat Med
1989
;
8
:
1051
–69.

11.

Spiegelman D, McDermott A, Rosner B. Regression calibration method for correcting measurement-error bias in nutritional epidemiology.

Am J Clin Nutr
1997
;
65
(suppl):
1179S
–86S.

12.

Finkelstein MM, Verma DK. Exposure estimation in the presence of nondetectable values: another look.

AIHAJ
2001
;
62
:
195
–8.

American Journal of Epidemiology Copyright © 2006 by the Johns Hopkins Bloomberg School of Public Health All rights reserved; printed in U.S.A.
Issue Section:
ORIGINAL CONTRIBUTIONS
Download all slides