Preserving perceptual distances in chromaticity diagrams

Abstract

INTRODUCTION

The graphical representation of color is an invaluable technique for describing experimental data and for modeling color thresholds (Chittka 1992; Backhaus 1998; Kelber et al. 2003; Endler and Mielke 2005) and has a long history of use in studies of human color vision (e.g., Maxwell 1860; MacLeod & Boynton 1979; Derrington et al. 1984). More recently, it has also been increasingly used to visualize the relationships between colors of importance to animal receivers (e.g., Osorio et al. 1999; Defrize et al. 2010). Such representations incorporate knowledge of the receiver's visual system into the calculation of a color's spatial position and so add a level of biological realism in the interpretation of color data compared with using visual system-independent analyses (e.g., Andersson and Prager 2006). The most commonly used diagrams, at least in vertebrate studies, are the triangular or tetrahedral chromaticity diagrams described by Kelber et al. (2003) and Endler and Mielke (2005) that allow the visualization of a color in terms of the relative quantum catch of the different photoreceptor classes in the retina, each of which is maximally sensitive to a different wavelength of light. They also allow the geometric description of the spatial relationships between color data and the extraction of spatial coordinates for subsequent analysis (Endler and Mielke 2005). However, because there is no straightforward relationship between the intercolor distance in a chromaticity diagram and the perceptual distance between those colors (Endler and Mielke 2005), in some situations, they may misrepresent the perceptual relationships between colors.

To illustrate this, I consider 1) the distance between pairs of colors in the commonly used triangular chromaticity diagram described in detail by Kelber et al. (2003) and 2) the perceptual distance between those colors determined from the noise-corrected model of Vorobyev and Osorio (1998), as described below. In the examples, I have used data on the visual system of the three-spined stickleback (Gasterosteus aculeatus). Sticklebacks are tetrachromatic, having 4 photoreceptor types with peak sensitivities, λ_max, at 605 (denoted L), 530 (M), 445 (S), and 360 nm (U) (Rowe et al. 2004), although in most of the examples below I only consider the L, M, and S cones for simplicity. Photoreceptor spectral sensitivity functions were calculated using the photopigment nomogram of Govardovskii et al. (2000) and incorporate transmission across the preretinal media (Boulcott 2003). Unless otherwise stated, I assume full-sunlight illumination conditions (modeled using a standard daylight-simulating illumination spectrum, D65; Wyszecki and Stiles 1982).

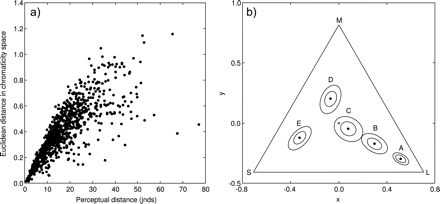
However, there is not necessarily a straightforward relationship between the Euclidean distance between data points in chromaticity space (i.e., ΔS_T) and the perceptual distance between them according to the Vorobyev–Osorio model (i.e., ΔS_VO) (Figure 1a). To illustrate this further, Figure 1b shows 5 data points, labeled A–E, plotted in a stickleback triangular chromaticity space representing the quantum catches of the L, M, and S cones. The Euclidean distance between A and B and between B and C is approximately equal (i.e., ΔS_T(A,B) ≈ ΔS_T(B,C) ≈ 0.25 units), although if the Vorobyev–Osorio model is applied to these data (assuming, for simplicity, an equal standard deviation of noise in each photoreceptor class of e_i = 0.05 and bright illumination conditions), then it can be shown, using the equations given above, that the noise-corrected levels of discriminability are unequal: ΔS_VO(A,B) = 17.9 jnds and ΔS_VO(B,C) = 12.6 jnds. The reason for this is that the contour representing an equal number of jnds around each point in chromaticity space is typically not circular, but elliptical, and moreover, the shape and size of a contour changes with the spatial position of a color (see the contours around each point in Figure 1b), generally getting larger and more circular as a color approaches the graph's origin (the achromatic, or “gray” point). The size of a contour is also affected by the level of noise in a photoreceptor (both the inner and the outer contours in Figure 1b assume an equal standard deviation of noise in each photoreceptor; however, the inner contours assumes that e_i = 0.05 and the outer contour assumes that e_i = 0.1).

Figure 1

Open in new tabDownload slide

(a) Relationship between the perceptual distance (jnds), calculated using the model of Vorobyev and Osorio (1998) (horizontal axis), and the Euclidean distance in triangular chromaticity space (sensu Kelber et al. 2003) (vertical axis) of 1000 randomly generated pairs of colors. (b) Five colors (black points, labeled A–E) plotted in a triangular chromaticity diagram, each surrounded by 2 contours representing the 3 jnds boundary (i.e., colors within a contour would have a perceptual distance from the corresponding color of <3 jnds, as calculated using the Vorobyev–Osorio model): both contours assume an equal standard deviation of noise in each photoreceptor of e_i = 0.05 (inner contour) or e_i = 0.1 (outer contour) (for details, see text). Contours were generated by finding the best-fitting ellipses (in the least-squares sense) to 1000 random colors that differed from the central color by 3 ± 0.01 jnds. The achromatic point is denoted by an “x” at the triangle's origin, and the 3 apices represent stimulation of a single 1 of the 3 cone classes contributing to color vision (labeled L, M, and S). Data for the visual system of the three-spined stickleback were used in generating the data in both plots; for full details, see text.

These examples illustrate that whether any 2 points in triangular (or indeed tetrahedral) chromaticity space are perceptually different cannot be reliably inferred directly from the chromaticity diagram itself, and so has implications for the geometric interpretation of color data within a chromaticity diagram. It would therefore be useful to have a chromaticity diagram in which the Euclidean distance between any 2 points, at any place in the chromaticity diagram, is directly proportional to the perceptual distance between them. The approach described here achieves this by deriving Cartesian coordinates for each color such that the Euclidean distance between any 2 points in this coordinate system is exactly equal to their perceptual distance in jnds, as calculated using the Vorobyev–Osorio model.

ALGORITHM

Values obtained using the Vorobyev–Osorio model describe perceptual distances between 2 colors (i.e., a single value of perceptual distance rather than 2 sets of coordinates, one for each color). In order to plot these data, spatial coordinates must be derived for each color based solely on the value of perceptual distance between each color pair. Perceptual distance data calculated by the Vorobyev–Osorio model allow the construction of such coordinates because any 3 colors can be arranged in a triangle such that length of each side is exactly equal to the jnd between the 2 connected colors at the triangle's vertices (i.e., if you know the jnds between colors A and B and between B and C, then the jnds between A and C can be determined geometrically). The algorithm used here determines the positions of each color in space using trilateration (i.e., determining position based on the geometry of triangles and circles or, in 3D space, spheres) and is described below. Matlab (The Mathworks, Natick, MA) and R (R Core Development Team) code for converting perceptual distances matrices into Cartesian coordinates is available as Supplementary Material.

Given a set of N colors (c₁, c₂, …, c_N), represented in terms of the quantum catch of n photoreceptors (where n = 3 or 4), an N × N matrix D can be created in which each entry d_ij represents the perceptual distance (in jnds) between colors i and j (as determined following Vorobyev and Osorio’s 1998 model). Cartesian coordinates can be determined from the matrix of perceptual distances, D, as follows:

The first color, c₁, is defined as having the Cartesian coordinates [x₁, y₁] = [0, 0]. (In practice, this point could have any arbitrary coordinates but placing it at the origin simplifies the calculations.)

As the distance between the first and second points is known from D, the coordinates of the second color, c₂, can be defined as [x₂, y₂] = [d_1,2, 0].

As there are always 2 potential solutions to this problem (because 2 circles centered on [x₁, y₁] and [x₂, y₂] will intersect at 2 discrete points), 1 of these 2 sets of coordinates, [x₃, y₃] or [x₃, −y₃], is chosen arbitrarily as the location of the third color.

Again, the final coordinates must be chosen arbitrarily from the 2 possible solutions, [x₄, y₄, z₄] or [x₄, y₄, −z₄]. Simple modifications would also allow coordinates for dichromatic systems to be derived, and in principle, the technique could be expanded to derive coordinates for systems with 5 or more photoreceptors (e.g., cabbage white butterflies, Pieris rapae, have at least 6 cone types making them putative hexachromats or pentachromats; Morehouse and Rutowski 2010), although they could not be visualized in their entirety because they would require more than 3 dimensions (Pike 2011).

In the examples given in this paper (Figures 2 and 3), the points in color space have been translated so that the achromatic point (i.e., stickleback gray) is at the origin and rotated so that they are orientated similarly to the triangular chromaticity diagram in Figure 1b. Neither of these transformations is strictly necessary, as the color data could still be plotted with an arbitrary origin and orientation; however, these transformations not only aid interpretation of the color data and the limitations of visual system that is detecting it (see next section) but also allows direct comparisons to be made with the same data plotted in triangular chromaticity space. (Note that, if additional points in space are needed for construction of a diagram, such as the location of the achromatic point, then this will need to be included in the matrix D, so that the perceptual distance from this point to all the data points can be determined, as this cannot easily be computed retrospectively.)

Figure 2

Open in new tabDownload slide

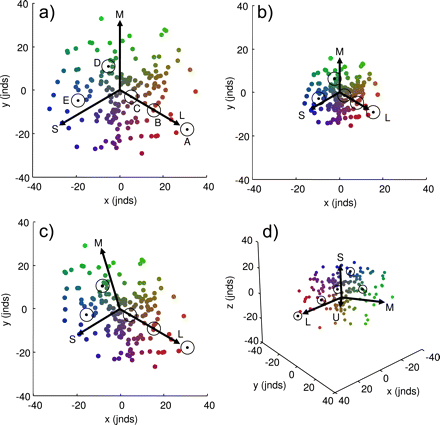
Color data plotted in the perceptual chromaticity diagram described in this paper. Each subplot contains the same 100 randomly generated colors. Also in each subplot are the 5 data points shown in Figure 1b (black points), each surrounded by a contour representing the 3 jnds boundary (as in Figure 1b), and arrows representing each of the cone classes contributing to the chromatic discrimination (labeled L, M, and S accordingly, as in Figure 1b); the additional arrow in (d) represents the sticklebacks ultraviolet-sensitive (U) cone. Please refer to the text for a full explanation of these plots.

Figure 3

Open in new tabDownload slide

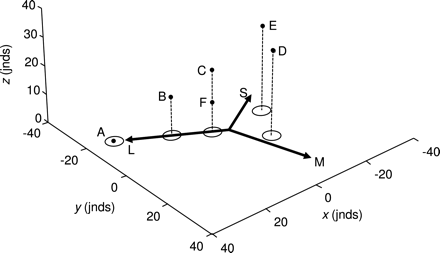
The 5 colors from Figure 1b (labeled A–E), plus an additional color, F, plotted in a perceptual color space that includes both chromatic and achromatic information (black points). The arrows and contours (ellipses) on the xy plane are exactly the same as those depicted in Figure 2c and therefore represent the relative chromatic information contained within each of the 6 colors. The z-axis represents the relative achromatic information contained within each color, such that the distance between colors along this axis is equal to their perceptual achromatic distance in jnds; the stems (dashed lines) simply allow the data points to be visualized more clearly in 3D space. Please refer to the text for a full explanation of this plot.

Caveat

Under the formulation used here, where cone responses are logged prior to the calculation of response differences (i.e., Δf_i = log(Q_iA/Q_iB) = log(Q_iA) − log(Q_iB)), situations where levels of cone stimulation approach zero (e.g., for particularly saturated colors) can cause problems because log(Q_i) is undefined when Q_i = 0. This causes no problems when all cones receive a moderate amount of stimulation (which is often the situation in practice) and can be overcome completely by using the unlogged differences instead (i.e., Δf_i = Q_iA − Q_iB), although this may not always be appropriate (Osorio et al. 2004).

DESCRIPTION OF THE PERCEPTUAL CHROMATICITY DIAGRAM

Some examples of the proposed perceptual chromaticity diagram are given in Figure 2, modeled using data for three-spined sticklebacks (Rowe et al. 2004; see INTRODUCTION). This chromaticity diagram achieves the goal of preserving perceptual distances between colors (i.e., the Euclidean distance between any 2 colors is exactly equal to their perceptual distance, in jnds). The axes units are therefore in jnds, although the values themselves are necessarily arbitrary since the set of data points can be rotated or translated in any direction while still preserving the Euclidean distance between colors. Note that the range of the x- and y-axes remains constant between subpanels in Figure 2 in order to better illustrate how changing levels of noise in the photoreceptors affect the spatial distribution of color data (see below). Each subpanel also shows the same set of 100 randomly generated colors, as well as the same 5 colors (A–E) that are represented in triangular chromaticity diagram in Figure 1b, each surrounded by a contour representing 3 jnds.

In each subpanel of Figure 2, arrows have been included to represent each of the cone classes contributing to the chromatic discrimination. Colors that lie on along one of these arrows will, in human perceptual terms, have the same hue, and the arrows therefore represent variation in the relative stimulation of a single cone class (i.e., low stimulation of a single given cone class will result in the color point falling near the foot of the relevant arrow; high stimulation will result in the color falling near its head). The actual length of these arrows is arbitrary (here they have been set to point at [0.9, 0.1, 0.1], [0.1, 0.9, 0.1], and [0.1, 0.1, 0.9], where these triplets are the quantum catches of the L, M, and S cones, respectively, normalized to the background irradiance), but what is important is the relative change in the arrows’ lengths and interarrow angles between graphs, as this is directly related to the level and asymmetry of noise in each of the receptor channels, as described below.

If we assume that the standard deviation of noise in each receptor channel is equal (e_i = 0.05 in Figure 2a and e_i = 0.1 in Figure 2b), then the arrows are of equal length, and the angle between any 2 arrows is equal. This is because all the receptors provide an equal weighting in the determination of perceptual distance. However, as the noise level in the receptors increases (as from Figure 2a to Figure 2b), the relative length of the arrows decreases because the greater level of noise means that it is harder for the visual system to discriminate between 2 given colors (i.e., they are now separated by a smaller jnd), thereby “squeezing” the colors together in space. Note that the contour representing the 3 jnd boundary around a color is circular (cf. the ellipses in Figure 1b), and remains the same size irrespective of changes that occur in the noise of a photoreceptor (e.g., between Figure 2a and Figure 2b), because of the direct relationship between Euclidean and perceptual distances.

It is unlikely that in a given animal, the noise in all photoreceptor channels will in fact be equal, and usually, there will be an asymmetry in the level of noise between photoreceptor classes (Vorobyev and Osorio 1998). In this case, both the relative lengths of the arrows and the angles between them will be unequal. This is illustrated in Figure 2c, where the standard deviation of noise in the S, M, and L cones is assumed (for illustration purposes) to be e_S = 0.08, e_M = 0.06, and e_L = 0.04, respectively. This has the effect of squeezing together (i.e., reducing the number of jnds between) colors along the S cone and, to a lesser extent, the M cone axes, and those colors that fall between these axes, whereas “stretching” (i.e., increasing the number of jnds between) colors that fall between the M and L cone axes. With this distribution of noise levels, it should therefore be easier for a stickleback to distinguish between reds and greens than between greens and blues. The geometry of these axes can therefore be used to infer aspects of the visual system, in terms of the noise in the color channels mediating perception, and can be used to directly compare visual systems experiencing different noise levels (e.g., as a result of changes in ambient light levels; Osorio et al. 2004).

Finally, a 3D version of this color space, for animals with 4 cone classes, can be drawn (Figure 2d), which, like the 2D version, can geometrically represent changes in receptor noise. The interpretation of this plot is in all respects identical to that described above because the z-axis units are also in jnds. The only difference is that there is an additional arrow representing the stickleback's ultraviolet-sensitive (U) cone (Rowe et al. 2004).

INCORPORATING LUMINANCE INFORMATION

When studies require the interpretation of a species’ ability to discriminate both chromatic and achromatic information, these are typically analyzed separately (e.g., Osorio et al. 2004). However, when an animal makes a visual discrimination, both the chromatic and achromatic aspects of a color are viewed and processed simultaneously. This underlies the ability of humans to discriminate between and categorize “colors” that are chromatically similar but differ in terms of luminance (brightness), such as orange and brown (brown is simply a dark orange) and red and pink (pink is a light red with reduced chroma) (e.g., Bartleson 1976). It is possible to add an independent achromatic axis to the perceptual chromaticity diagram described above, allowing relative variation in both the chromatic and the achromatic aspects of a color (or colors) to be visualized simultaneously (Figure 3).

Colors that are chromatically identical but differ in perceived luminance can now be visually differentiated (e.g., points C and F in Figure 3) and the resulting Cartesian coordinates used in statistical models (e.g., Endler and Mielke 2005), providing a test of overall perceptual differences between color stimuli. (Note that exactly the same procedure can be used to incorporate luminance information into a 4-cone perceptual color space, and thereby derive Cartesian coordinates for further analyses, although this information cannot be visualized directly because it requires more than 3 dimensions; Pike 2011.) However, because the achromatic and chromatic components of a color are probably processed via different neural mechanisms and are often used independently (e.g., animals may respond to variation in luminance independently of chromaticity and vice versa) (Osorio and Vorobyev 2005), this combined model may not always be appropriate.

CONCLUSIONS

I have described a simple method for converting perceptual distances between colors, as determined using the popular noise-corrected model of Vorobyev and Osorio (1998), into a graphical representation of colors in a chromaticity diagram that exactly preserves perceptual distances between them. This brings a number of benefits over the more commonly used triangular and tetrahedral chromaticity diagrams (sensu Kelber et al. 2003; Endler and Mielke 2005). First, it allows data that previously existed only as a matrix of perceptual distances to be assigned useful coordinates. This not only allows the data to be plotted and visualized but the coordinates themselves can be used directly in statistical analyses that require Cartesian coordinates as inputs (e.g., Endler and Mielke 2005). Second, it allows color data to be visualized in chromaticity diagrams from which meaningful insights can be gained by looking at the spatial positioning of the data points (e.g., to interpret the “direction” of the difference between 2 colors, which cannot be inferred from the absolute jnd value; Delhey et al. 2010). This allows for a more intuitive way of representing and interpreting color data that enhances the level of biological realism. Moreover, it allows the effects that changing receptor noise levels (e.g., when comparing low and high illumination conditions; Osorio et al. 2004), and the effect this has on chromatic discrimination, to be readily visualized as changes in the geometry of the data points. Third, with modifications, it is possible to visualize both the chromatic and the achromatic aspects of a perceived color within a single diagram, allowing inferences to be drawn regarding their composite perceptual distance from other colors and the derivation of composite spatial coordinates for use in statistical models (e.g., Endler and Mielke 2005).

Perceptual modeling has become very popular in studies of animal color vision and is an invaluable tool for helping to understand color vision–mediated behavior. However, these models only provide abstractions of real visual systems, which are rarely validated against behavioral data and are subject to limitations in our understanding of the particular visual system we are modeling. For example, although we have an increasingly good understanding of photoreceptor sensitivities for a wide range of species, we have a poorer understanding of the levels of noise present in these receptor mechanisms (prerequisites for using the Vorobyev–Osorio model). Care must therefore be taken when interpreting data from perceptual models, and it may be prudent to present a number of different visual scenarios before drawing firm conclusions (e.g., as has been done in studies which explore perception over a range of plausible receptor noise levels; Osorio et al. 2004; Langmore et al. 2009). Being able to graphically represent these different scenarios, using models such as the one described here, would therefore greatly aid their interpretation.

SUPPLEMENTARY MATERIAL

Supplementary material can be found at http://www.beheco.oxfordjournals.org/.

FUNDING

This work was supported by a Natural Environment Research Council fellowship (NE/F016514/2).

References