Search
Close
Search
Advanced Search
Search Menu

Abstract

A computer simulation study has been made of the accuracy of estimates of Θ = 4Neμ from a sample from a single isolated population of finite size. The accuracies turn out to be well predicted by a formula developed by Fu and Li, who used optimistic assumptions. Their formulas are restated in terms of accuracy, defined here as the reciprocal of the squared coefficient of variation. This should be proportional to sample size when the entities sampled provide independent information. Using these formulas for accuracy, the sampling strategy for estimation of Θ can be investigated. Two models for cost have been used, a cost-per-base model and a cost-per-read model. The former would lead us to prefer to have a very large number of loci, each one base long. The latter, which is more realistic, causes us to prefer to have one read per locus and an optimum sample size which declines as costs of sampling organisms increase. For realistic values, the optimum sample size is 8 or fewer individuals. This is quite close to the results obtained by Pluzhnikov and Donnelly for a cost-per-base model, evaluating other estimators of Θ. It can be understood by considering that the resources spent collecting larger samples prevent us from considering more loci. An examination of the efficiency of Watterson's estimator of Θ was also made, and it was found to be reasonably efficient when the number of mutants per generation in the sequence in the whole population is less than 2.5.

coalescent, maximum likelihood, population size, sampling design

Introduction

The availability of molecular sequencing at prices that even population biologists can afford has brought into existence new methods of estimation of population parameters. Sequence samples from populations enable one to make an estimate of the coalescent tree of genes connecting these sequences. I have argued (Felsenstein 1992a) that these enable a substantial increase in the accuracy of estimation of population parameters like Θ = 4Neμ, the product of effective population size, and the neutral mutation rate per site. (This is usually expressed as θ, the neutral mutation rate per locus but is perhaps better thought of in terms of the neutral mutation rate per site.)

Fu and Li (1993) analyzed my claim further. They developed some approximations to the accuracy of maximum likelihood estimation of Θ. I will show below that these are remarkably good approximations, better than one might have expected. My argument had assumed that an infinite number of sites could be examined and that the coalescent tree was therefore precisely known in both topology and coalescence times. Fu and Li (1993) did not assume that the coalescence times were precisely known, but they did assume that we could infer the substitutions on each branch of the tree and that in addition we could assign those according to which coalescent interval they occurred in. Their result made use of the total number of substitutions in each coalescent interval. Although it did not use the tree topology, it is hard to see how one could have the assignment to coalescent interval without an assignment to branch of the topology as well. Their approximations were therefore necessarily overoptimistic, though not as much as mine had been. They found that there was an increase in accuracy of estimation using likelihood methods but that it would not be as large an increase as I had claimed.

Fu (1994) developed a method which makes a UPGMA estimate of the coalescent tree and constructs a best linear unbiased estimate conditional on that being the correct tree. In his simulations using the infinite-sites model, his BLUE method achieved variances nearly as low as the Fu and Li lower bound. It is not obvious from this whether it would perform as well with data from an actual finite-sites DNA sequence model of evolution, where the tree is bound to be harder to infer. Nevertheless, the good behavior of BLUE suggests that a full likelihood method based on summing over all coalescent trees might do almost as well as the Fu-Li lower bound.

In the present paper, the results of a computer simulation of coalescent likelihood estimates of Θ will be described, demonstrating that one of Fu and Li's optimistic approximation formulas does do a good job of calculating the accuracy of maximum likelihood estimates of Θ. Formulas based on it can then to be used to investigate optimal design of experiments for estimating Θ. The results turn out to be quite similar to those of Pluzhnikov and Donnelly (1996), who evaluated optimal designs using earlier methods of estimation of Θ. Their simulations explicitly check the effect of the number of loci, finding that the accuracy is proportional to the number of loci, as expected and as assumed here. These allow one to see how effectively accuracy can be increased by sampling more sites, more sequences, or more unlinked loci. The results, which strongly back collecting more loci rather than more sites or more sequences, can be argued to be intuitively reasonable.

Likelihoods with Coalescents

In population samples at a locus, there are likely to be only a few sites segregating within the population so that the tree topology is unlikely to be known well. Monte Carlo integration methods have been developed by Griffiths and Tavaré (1994a, 1994b, 1994c) and by Kuhner, Yamato, and Felsentein (1995) to address this problem.

The basic equation for likelihood estimation of Θ is (Felsenstein 1988, 1992b)
\[L{=}{{\sum}_{G{\ast}}}\mathrm{Prob}(G{\ast}{\vert}N_{e})\mathrm{Prob}(D{\vert}G{\ast},\mathrm{{\mu}}),\]
(1)
where Ne is the effective population size, μ the neutral mutation rate per site, and G* indexes all possible coalescent trees of gene copies, including all possible trees and all possible branch lengths of those clocklike trees. The summation over trees is, when summing over different branch lengths, actually a multiple integration. This formula might, at first sight, seem to allow separate estimation of Ne and μ, but this is an illusion. The coalescent trees G* have their branch lengths given in generations. But our molecular observations only tell us about the number of sites differing, not about the number of generations separating two sequences. The probability
\(\mathrm{Prob}(G{\ast}{\vert}N_{e})\)
of the coalescent genealogy is given by the diffusion-equation approximation of Kingman (1982a, 1982b, 1982c). When the Kingman coalescent is used, there turns out to be a precise trade-off: the effect on
\(\mathrm{Prob}(G{\ast}{\vert}N_{e})\)
of multiplying Ne by a constant is exactly offset by the effect on
\(\mathrm{Prob}(D{\vert}G{\ast},\mathrm{{\mu}})\)
of dividing μ by the same constant. If we instead express the coalescent tree of gene copies so that its branch lengths are the expected numbers of neutral mutations per site, it can be denoted by G and equation (1) becomes
\[L{=}{{\sum}_{G}}\mathrm{Prob}(G{\vert}{\Theta})\mathrm{Prob}(D{\vert}G)\]
(2)
without loss of generality. Once again, the summation is assumed to be over all tree topologies and to be as well integration over all possible branch lengths of those trees. The Kingman prior for a tree whose branch lengths are given in expected neutral mutations per site turns out to be a function of Θ = 4Neμ rather than separately of Ne and μ. (The factor of 4 in Θ is included to simplify the expressions in the Kingman prior.)

The summation in equation (2) is over all possible tree topologies with integration over all possible branch lengths. In fact, the sum is actually over all possible “labeled histories” (Edwards 1970), entities that take all possible tree topologies and further distinguish between the time orderings of interior nodes. There are a huge number of these. For population samples of only 10 sequences, there are 2.571 × 109 labeled histories (Edwards 1970). Within each of them there are nine coalescence times that can be varied from zero to infinity. So to evaluate equation (2) exactly in that case, it requires us to compute more than 2.571 × 109 nine-dimensional integrals.

Most of the labeled histories and most values of the branch lengths may conflict rather strongly with the sequence data and thus contribute little to equation (2). It is possible to obtain an approximate integration of equation (2) by sampling a large number of values of coalescent trees, concentrating the sampling on ones which contribute substantially to the integral. Two major approaches exist. Griffiths and Tavaré (1994a, 1994b) have developed a method that samples histories of coalescence and mutation (rather than sampling trees which have no mutational events specified but do have times of coalescence specified). Their method has the great advantage that successive samples of histories are independent. Kuhner, Yamato, and Felsentein (1995) have developed a method that uses Markov chain Monte Carlo (MCMC) sampling to draw genealogical trees G in a way that is autocorrelated, so that the tree G wanders through the space of possible trees, concentrating on the regions that contribute most to the integral (2). Another approximate alternative to these two methods is Fu's (1994) method, which uses a single estimated coalescent tree but applies a simulation-based correction formula to approximately account for the effect of the other possible coalescent trees. Sampling methods involving independent sampling or MCMC have been increasingly applied to these problems; some of the newer programs use Bayesian inference (e.g., Wilson, Weale, and Balding 2003), which will not be directly considered here, as it requires specification of a prior distribution on the parameters. However, when the amount of data is large, Bayesian methods should give results similar to maximum likelihood methods.

A Measure of Accuracy

In this paper, I have used the COALESCE program of Kuhner, Yamato, and Felsentein (1995), version 1.3, to make maximum likelihood estimates from simulated data to infer the accuracy of Monte Carlo maximum likelihood estimation of Θ and compare it to accuracy computed from the formulas of Fu and Li (1993). I do not expect that the present results would be different if another computational approach, such as the method of Griffiths and Tavaré (1993), had been applied instead. We measure accuracy of estimation by the inverse of the squared coefficient of variation (hence

\({\Theta}^{2}/\mathrm{Var}({\hat{{\Theta}}})\)
⁠) of the estimate of the single parameter. The inverse of the variance is a natural measure because it is expected to be proportional to the number of independent items of information used in the estimation. It is proportional to the Fisher information of Θ. The accuracy scales this quantity by the square of the expected value of Θ.

Fu and Li (1993) gave approximate formulas for the variance of the maximum likelihood estimate of θ. Consider their approximation for the variance of their θm estimator. One can easily recast equation (28) of their paper to give the accuracy of maximum likelihood estimation of Θ. If there are L unlinked loci, n sampled sequences at each, with s sites, the accuracy of estimation implied by their equations is
\[\frac{{\Theta}^{2}}{\mathrm{Var}({\hat{{\Theta}}})}{=}L{{\sum}_{k{=}2}^{n}}\frac{1}{(1{+}\frac{k{-}1}{s{\Theta}})}.\]
(3)
Figure 1 shows the accuracy of maximum likelihood estimation computed using their approximation for two values of Θ, 0.01 and 0.003, for one locus and for three sample sizes, 20, 50, and 100 sequences.
FIG. 1.—
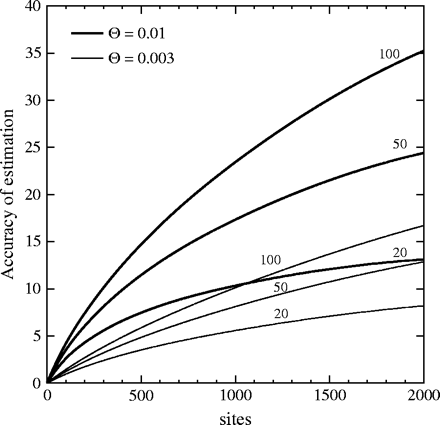
Accuracy of maximum likelihood estimation predicted by Fu and Li's approximation. Two values of Θ, 0.003 and 0.01, are shown. The accuracy is shown as a function of number of sites and of the number of sequences sampled (the numbers next to the curves).
Open in new tabDownload slide

Accuracy of maximum likelihood estimation predicted by Fu and Li's approximation. Two values of Θ, 0.003 and 0.01, are shown. The accuracy is shown as a function of number of sites and of the number of sequences sampled (the numbers next to the curves).

The accuracy of maximum likelihood estimation can be seen to increase with the number of sites, the number of sequences, and the value of Θ. It will also increase (proportionately) to the number of unlinked loci, which is not shown in this figure 1. Note that the increase with the sample size and with the number of sites is not proportional to the amount of data but shows diminishing returns. A brief consideration of equation (3) will show that the accuracy of maximum likelihood estimation reaches an asymptote at n − 1 with large numbers of sites and that it rises as approximately the logarithm of the sample size.

Note also that the accuracy of maximum likelihood estimation is smaller when Θ is smaller. Note that accuracy, as defined here, is a function of sΘ and thus approaches the same asymptote with increase of Θ as it does with increase of s.

We will be looking at the increase in accuracy of maximum likelihood estimation of Θ as we add sites, sequences, or unlinked loci, so that seeing whether the curve rises proportionally to these will be useful.

A Simulation Study

Fu and Li's formula is an approximation. It comes from assumptions which they note are overly optimistic, intended only to place a bound on the accuracy. To see how close these approximations may be, I have carried out a simulation study. Its design was hierarchical. For each parameter combination, 200 coalescent trees were simulated, at the given value of Θ. The trees consisted of tree topologies together with coalescent intervals expressed in units of expected mutations per site. Along each of the trees two replicates were made of the evolution of a single locus according to a Kimura (1980) two-parameter model of DNA change, with a transition/transversion ratio of 2.0. For each of these data sets, two runs of COALESCE were made. The design of the simulation thus allows us to separate the effect of coalescent trees, mutational events, and runs of the simulation program. Three sample sizes (20, 50, and 100) were examined along with five different numbers of sites (100, 200, 500, 1000, and 2000). Two different values of Θ were used (0.003 and 0.01). These values are larger than is often biologically reasonable; they are used here because they allow simulations to be done in a reasonable amount of time. There was no recombination; the sites in each locus were in effect completely linked. No attempt was made to simulate different numbers of independent loci because the complete independence of the estimates from independent loci should make the accuracy of maximum likelihood estimation straightforwardly proportional to the number of loci.

Bias

The simulations can be examined to see whether the estimates of Θ were biased. Maximum likelihood estimates are often biased, with the bias decreasing as the amount of data increases. With a sample of two sequences, there is a very small chance that the two sequences are diverged at more than 75% of their sites, which would lead to an infinite estimate of the divergence time and an infinite estimate of Θ. Thus, in theory, maximum likelihood estimates of Θ should be infinitely strongly biased. In practice, these cases of more than 75% divergence may almost never occur, but the estimate of Θ may still be biased. This behavior in a tiny fraction of cases is not incompatible with the estimation being consistent as the fraction of cases in which there is more than 75% divergence declines rapidly with larger sample size, and the estimate converges to the true value of Θ.

In the simulations with Θ = 0.01, the mean of the estimate of Θ varied across the 15 cases between 0.00910183 and 0.01003190, with a median of 0.00975720, which is about 2.4% low. In the simulations with Θ = 0.003, the mean estimates of Θ varied between 0.0025166 and 0.00297930, with a median of 0.00284698, which is about 5.1% low. Thus, there was some underestimation of Θ, possibly connected with cases in which the Markov chains suffered “fatal attraction” to zero. There was no particular pattern as to which cases suffered the most from this underestimation, though the cases with 100 sites gave lower estimates of Θ than did the others.

Variance

The hierarchical design lends itself to an analysis of variance. Doing this assumes that the effects of trees, mutational events, and runs on the estimates are additive. To be a completely efficient way of analyzing the data, it would also require that the values be multivariate normally distributed. As both of these are unlikely to be true, I have not tried to do any statistical tests on the results of the analyses of variance but merely tried to derive point estimates of the accuracy of maximum likelihood estimation. A separate analysis of variance was performed for each combination of the sample size, number of sites, and value of Θ.

The model for the analysis of variance is a two-level hierarchical analysis of variance with random effects:
\[Y{=}\mathrm{{\mu}}{+}\mathrm{{\alpha}}_{i}{+}\mathrm{{\beta}}_{ij}{+}\mathrm{{\varepsilon}}_{ijk},\]
(4)
where μ is the expectation of the estimate of Θ, αi is the random effect of the i-th tree, βij is the random effect of the j-th set of mutational events simulated along the i-th tree, and εijk, the error term, is the effect of the k-th replicate Metropolis-Hastings run done on the j-th locus from the i-th tree. The variances are:
\[\mathrm{{\sigma}}_{Y}^{2}{=}\mathrm{{\sigma}}_{T}^{2}{+}\mathrm{{\sigma}}_{L(T)}^{2}{+}\mathrm{{\sigma}}_{R(TL)}^{2}.\]
(5)
The analysis of variance does not assume that the effects of trees and of mutational events are additive, for
\(\mathrm{{\sigma}}_{L(T)}^{2}\)
contains the variance of any interaction between tree and mutational events, as well as the variance of the effect of the mutational events. There are, of course, assumptions of homogeneity of variance in this analysis, which I cannot completely defend. The objective is to estimate the variance of the estimate of Θ. If the Metropolis-Hastings runs were infinitely long, then they would (in theory) arrive at the same maximum likelihood estimate of Θ in each replicate run. The variance of that estimate will then be
\[\mathrm{Var}({\hat{{\Theta}}}){=}\mathrm{{\sigma}}_{T}^{2}{+}\mathrm{{\sigma}}_{L(T)}^{2}.\]
(6)
We cannot run the programs for an infinitely long time, but we can estimate the variance components and use these estimates to infer the theoretical variance of the maximum likelihood estimator using equation (6). Table 1 shows the analysis of variance formulas. The conventions are the usual ones: dot subscripts indicate that the mean has been taken, t is the number of trees, l the number of unlinked loci per tree, and r the number of runs per locus.
Table 1

Analysis of Variance for a Set of Runs for One Combination of Parameter Values

Effect
Sum of Squares
df
Expectation of Mean Square
Trees
\(SS(T){=}{\sum}_{i}{\sum}_{j}{\sum}_{k}(x_{i..}{-}x_{{\ldots}})^{2}\)
(t − 1)
\(\mathrm{{\sigma}}_{R(TL)}^{2}{+}r\mathrm{{\sigma}}_{L(R)}^{2}{+}rl\mathrm{{\sigma}}_{T}^{2}\)
Loci
\(SS(L){=}{\sum}_{i}{\sum}_{j}{\sum}_{k}(x_{ij.}{-}x_{i..})^{2}\)
t(l − 1)
\(\mathrm{{\sigma}}_{R(TL)}^{2}{+}r\mathrm{{\sigma}}_{L(T)}^{2}\)
Runs
\(SS(R){=}{\sum}_{i}{\sum}_{j}{\sum}_{k}(x_{ijk}{-}x_{ij.})^{2}\)
tl(r − 1)
\(\mathrm{{\sigma}}_{R(TL)}^{2}\)
Total
\(SS(Y){=}{\sum}_{i}{\sum}_{j}{\sum}_{k}(x_{ijk}{-}x_{{\ldots}})^{2}\)
tlr − 1
Effect
Sum of Squares
df
Expectation of Mean Square
Trees
\(SS(T){=}{\sum}_{i}{\sum}_{j}{\sum}_{k}(x_{i..}{-}x_{{\ldots}})^{2}\)
(t − 1)
\(\mathrm{{\sigma}}_{R(TL)}^{2}{+}r\mathrm{{\sigma}}_{L(R)}^{2}{+}rl\mathrm{{\sigma}}_{T}^{2}\)
Loci
\(SS(L){=}{\sum}_{i}{\sum}_{j}{\sum}_{k}(x_{ij.}{-}x_{i..})^{2}\)
t(l − 1)
\(\mathrm{{\sigma}}_{R(TL)}^{2}{+}r\mathrm{{\sigma}}_{L(T)}^{2}\)
Runs
\(SS(R){=}{\sum}_{i}{\sum}_{j}{\sum}_{k}(x_{ijk}{-}x_{ij.})^{2}\)
tl(r − 1)
\(\mathrm{{\sigma}}_{R(TL)}^{2}\)
Total
\(SS(Y){=}{\sum}_{i}{\sum}_{j}{\sum}_{k}(x_{ijk}{-}x_{{\ldots}})^{2}\)
tlr − 1

NOTE.—df, degrees of freedom. This is used to estimate the variance components rather then to test whether they are nonzero. The usual analysis of variance convention is followed of indicating by dots those subscripts over which the mean has been taken.

Open in new tab
Table 1

Analysis of Variance for a Set of Runs for One Combination of Parameter Values

Effect
Sum of Squares
df
Expectation of Mean Square
Trees
\(SS(T){=}{\sum}_{i}{\sum}_{j}{\sum}_{k}(x_{i..}{-}x_{{\ldots}})^{2}\)
(t − 1)
\(\mathrm{{\sigma}}_{R(TL)}^{2}{+}r\mathrm{{\sigma}}_{L(R)}^{2}{+}rl\mathrm{{\sigma}}_{T}^{2}\)
Loci
\(SS(L){=}{\sum}_{i}{\sum}_{j}{\sum}_{k}(x_{ij.}{-}x_{i..})^{2}\)
t(l − 1)
\(\mathrm{{\sigma}}_{R(TL)}^{2}{+}r\mathrm{{\sigma}}_{L(T)}^{2}\)
Runs
\(SS(R){=}{\sum}_{i}{\sum}_{j}{\sum}_{k}(x_{ijk}{-}x_{ij.})^{2}\)
tl(r − 1)
\(\mathrm{{\sigma}}_{R(TL)}^{2}\)
Total
\(SS(Y){=}{\sum}_{i}{\sum}_{j}{\sum}_{k}(x_{ijk}{-}x_{{\ldots}})^{2}\)
tlr − 1
Effect
Sum of Squares
df
Expectation of Mean Square
Trees
\(SS(T){=}{\sum}_{i}{\sum}_{j}{\sum}_{k}(x_{i..}{-}x_{{\ldots}})^{2}\)
(t − 1)
\(\mathrm{{\sigma}}_{R(TL)}^{2}{+}r\mathrm{{\sigma}}_{L(R)}^{2}{+}rl\mathrm{{\sigma}}_{T}^{2}\)
Loci
\(SS(L){=}{\sum}_{i}{\sum}_{j}{\sum}_{k}(x_{ij.}{-}x_{i..})^{2}\)
t(l − 1)
\(\mathrm{{\sigma}}_{R(TL)}^{2}{+}r\mathrm{{\sigma}}_{L(T)}^{2}\)
Runs
\(SS(R){=}{\sum}_{i}{\sum}_{j}{\sum}_{k}(x_{ijk}{-}x_{ij.})^{2}\)
tl(r − 1)
\(\mathrm{{\sigma}}_{R(TL)}^{2}\)
Total
\(SS(Y){=}{\sum}_{i}{\sum}_{j}{\sum}_{k}(x_{ijk}{-}x_{{\ldots}})^{2}\)
tlr − 1

NOTE.—df, degrees of freedom. This is used to estimate the variance components rather then to test whether they are nonzero. The usual analysis of variance convention is followed of indicating by dots those subscripts over which the mean has been taken.

Open in new tab
Using the estimates of
\(\mathrm{{\sigma}}_{T}^{2}\)
and
\(\mathrm{{\sigma}}_{L(T)}^{2}\)
from this analysis of variance, we infer the accuracy of maximum likelihood estimation as
\[\frac{{\Theta}^{2}}{\mathrm{Var}({\hat{{\Theta}}})}{=}\frac{{\Theta}^{2}}{\mathrm{{\sigma}}_{T}^{2}{+}\mathrm{{\sigma}}_{L(T)}^{2}}.\]
(7)

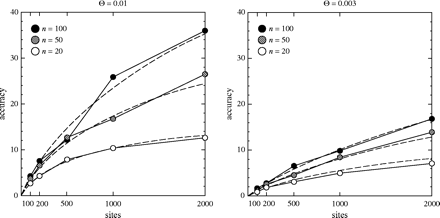
Figure 2 shows these empirical accuracies. They are larger as a result of our elimination of the runs variance component. If the runs variance component is included, the accuracy of estimation is somewhat smaller.

FIG. 2.—
Accuracy of maximum likelihood estimation measured empirically by simulation. The points show the accuracies from the simulation; the curves are the accuracies from Fu and Li's approximation. The empirical accuracy of maximum likelihood estimation is projected for infinitely long runs of the Metropolis-Hastings sampler by eliminating the between-runs variance component from the variance of the estimates of Θ.
Open in new tabDownload slide

Accuracy of maximum likelihood estimation measured empirically by simulation. The points show the accuracies from the simulation; the curves are the accuracies from Fu and Li's approximation. The empirical accuracy of maximum likelihood estimation is projected for infinitely long runs of the Metropolis-Hastings sampler by eliminating the between-runs variance component from the variance of the estimates of Θ.

The message of the simulations is simple: the Fu and Li approximation is remarkably good. We have reason to suspect that it will be too optimistic, but the simulations show that it is not far off. This is surprising as it assumes that we can assign all mutations to their proper coalescence interval, which even the Metropolis-Hastings sampler will not be able to do. For example, a mutation on a long exterior branch of the tree could have occurred in any of the coalescence intervals through which that branch passes, and no use of likelihood will be able to make that assignment more precise. Yet the approximations based on the assumption that we can assign the mutation to its proper interval turn out to work.

A Further Approximation

The formula of Fu and Li (1993), as reworked here, is a summation with a number of terms nearly as large as the population sample size. It would be helpful to have a formula that is more compact. The integral method in summation of series is easily applied to approximate and bound the sum in equation (3):
\begin{eqnarray*}&&L{{\int}_{2}^{n{+}1}}\frac{1}{(1{+}\frac{x{-}1}{s{\Theta}})}{\,}\mathrm{d}x\\&&{\leq}L{{\sum}_{k{=}2}^{n}}\frac{1}{(1{+}\frac{k{-}1}{s{\Theta}})}{\leq}L{{\int}_{1}^{n}}\frac{1}{(1{+}\frac{x{-}1}{s{\Theta}})}{\,}\mathrm{d}x.\end{eqnarray*}
(8)
The integrals are easily evaluated to yield:
\begin{eqnarray*}&&Ls{\Theta}{\,}\mathrm{ln}\left(\frac{s{\Theta}{+}n}{s{\Theta}{+}1}\right)\\&&{\leq}L{{\sum}_{k{=}2}^{n}}\frac{1}{(1{+}\frac{k{-}1}{s{\Theta}})}{\leq}Ls{\Theta}{\,}\mathrm{ln}\left(\frac{s{\Theta}{+}n{-}1}{s{\Theta}}\right).\end{eqnarray*}
(9)
For simplicity, we will use the upper bound as a closed-form approximation to equation (3). When s is large, the two limits are very close; for L = 1, they seem never to differ by more than 1.

Implications for Design of Studies

If the Fu and Li approximations are reasonably good, they can be used to guide us in the design of research projects. If we are estimating Θ and seeking to make its coefficient of variation as small as possible, we may be faced with the alternative possibilities of adding more sites, adding more samples from the population, or adding more unlinked loci. These of course will not be equal in cost. Pluzhnikov and Donnelly (1996) have made the pioneering effort here, using formulas for Watterson's (1975) and Tajima's (1983) estimators of Θ. Our formulas can be compared with theirs for the case where there is no recombination within sequences.

Adding More Sites

If we use equation (3) or equation (9) and let s → ∞, we will find that the accuracy of estimation approaches (n − 1)L asymptotically. Thus, in cases with one locus, when n = 20, the accuracy of estimation can never exceed 19; when n = 50, it can never exceed 49; and when n = 100, it can never exceed 99. For the larger sample sizes these limits are far above the curves in figure 1. For the smaller sample sizes they are being approached even with the numbers of sites on that figure. For n = 20, the accuracy of estimation is already halfway to the asymptote when we have 1,000 sites, and for n = 50, it is more than one-third of the way. With an infinite number of linked sites, we can make an excellent estimate of the coalescent tree. But that tree is itself stochastic, so that adding sites cannot subdue that part of the stochastic variation. The implication is that adding sites to a study, by extending the sequencing of the molecules, is a very limited way to add information.

Adding More Samples

Adding sample size, there is no asymptote. However, the accuracy of maximum likelihood estimation rises rather slowly with increased sample size. The approximations in equation (9) show that the increase of accuracy of maximum likelihood estimation with sample size is ultimately logarithmic. This is borne out by figure 1. For example, with Θ = 0.01, 500 sites and 20 samples, the accuracy of maximum likelihood estimation is 9.17. When the sample size increases from 20 to 50, the accuracy of maximum likelihood estimation is not 2.5 times higher, but is 15.37, which is only 68% higher. When it increases from 50 to 100, the accuracy of estimation does not double, but it increases only to 20.52, which is a rise of only 34%. Ultimately, the rate of increase will become logarithmic. To double the accuracy of maximum likelihood estimation, logarithmic increase suggests that one would have to approximately square the sample size. This behavior begins to be approached for large sample sizes. For example, to double the accuracy of maximum likelihood estimation for Θ = 0.01 and 500 sites from a sample size of 1,000, one must increase the sample size to 200,000.

Optimal Design of Studies

A Cost-Per-Base Model

Using the right-hand side of equation (9), we can optimize the design of studies, given that the objective is to improve the accuracy of maximum likelihood estimation and given a model of costs. Naively, we could, for example, take the cost of a study to be a simple function of the number of unlinked loci, the total number of sites sequenced, and the sample size. For example, we could assume that the cost of adding a new locus to the study is CL, the cost of adding an additional sample to the study is CS, and the cost of sequencing one more base is CB for each sample and locus. A sample is assumed to be an individual haploid genotype from which L loci are sequenced. Then the total cost of a study that has L unlinked loci, sample size n, and s sites would be
\[C{=}LC_{L}{+}nC_{S}{+}LnsC_{B}.\]
(10)
Pluzhnikov and Donnelly (1996) used a cost function in their study which was simply (in our notation) LnsCB. In effect, this assumes that costs for developing new loci and for sampling organisms can be neglected.
The accuracy of maximum likelihood estimation per unit cost is given by dividing the right-hand side of equation (9) by this cost:
\[Q{=}\frac{Ls{\Theta}{\,}\mathrm{ln}(1{+}\frac{n{-}1}{s{\Theta}})}{LC_{L}{+}nC_{S}{+}LnsC_{B}}.\]
(11)
In the special case where the only cost is the cost of sequencing per base, CB, this equation reduces to
\[Q{=}\frac{{\Theta}{\,}\mathrm{ln}(1{+}\frac{n{-}1}{s{\Theta}})}{nC_{B}}.\]
(12)
In this case, L has disappeared from the equation and s is present only in the denominator inside the logarithm. Decreasing s always increases the accuracy, so that the optimal value s = 1. L is then set by making it just big enough to achieve the target cost. In this special case, the ideal design is to have a very large number of unlinked loci, each one base long. There is a nontrivial optimization problem in choosing n, but the model of cost is not very realistic. Even the more general cost-per-base model is not sufficiently realistic.

A Cost-Per-Read Model

Presently, sequencing machines have a cost-per-“read,” and sequencing fewer bases does not save anything. However, extending the length of the sequence beyond the length of a read incurs a cost in the cost of extra reads plus the cost of development of primers for these extra reads. This is similar to the cost incurred in developing a new locus; I will assume that these are equal. Suppose that we have a total (across loci) of R reads per individual sampled, and these are spread among L unlinked loci. Each read is sR bases long and carries data from nR sampled individuals. Sample size is n, as before, so that the total number of reads that must be done across all individuals is (n/nR)R. For the moment, we ignore the fact that this should be an integer.

The cost may then be taken to be
\[C{=}RC_{L}{+}nC_{S}{+}(n/n_{R})RC_{R},\]
(13)
where CL is the cost of developing a new locus or an additional read of a locus, CS is the cost of collecting each sample, and CR is the cost of a single read. The accuracy per unit cost is, using equation (9) with s = (R/L)sR,
\[Q{=}\frac{Rs_{R}{\Theta}{\,}\mathrm{ln}(1{+}\frac{L(n{-}1)}{Rs_{R}{\Theta}})}{RC_{L}{+}nC_{S}{+}n/n_{R}RC_{R}}.\]
(14)
Maximizing Q will give the same result as maximizing the accuracy for a fixed cost. It can be seen immediately that L appears in only one place in the equations and that Q must increase with increase in the number of loci. Thus, to maximize Q, we should want L to be as large as possible, which in this case means being equal to R, so that there is a different locus for each read.

If we examine dependence on n, the pattern is not as clear. The optimum value of n is neither infinite nor is it to make n as small as possible. In such a case, we cannot simply optimize Q. Instead we will try, for different values of the sample size n, to find the value of R which achieves the target cost and then to find the accuracy of estimation that is achieved by those values. Plotting this against n discloses the optimum value of n.

As an example, suppose that we have sR = 600 and CL = 40. Some colleagues of mine report that they are charged per lane rather than per read by sequencing services, which is as if nR = 1, which will be assumed in our calculations. We will take CR = 6. These costs are close to the ones they report, in US dollars. Suppose that Θ = 0.003 and that the cost per sample, CS = 0.10.

Given a total cost for the study which is fixed at (say) US$ 1000, we can try different values of n and for each, compute what number of total reads per individual, R can be accomplished with this total cost. Solving equation (13) for R we get
\[R{=}\frac{C{-}nC_{S}}{C_{L}{+}nC_{R}}.\]
(15)
(We have ignored the fact that R must be an integer in this calculation). For each such value of R, we can take L = R and then simply use
\[A{=}Rs_{R}{\Theta}{\,}\mathrm{ln}\left(1{+}\frac{(n{-}1)}{s_{R}{\Theta}}\right)\]
(16)
to compute what accuracy can be achieved. The results are shown in table 2.
Table 2

Numbers of Unlinked Loci and Reads (R) and Accuracy Achieved (A) for Different Sample Sizes When Costs Total US$ 1000

n
R
A
219.2315.291
317.2423.182
415.6227.575
514.2830.073
613.1531.461
712.1932.165
811.3532.435
910.6332.421
109.9932.219
206.2427.476
304.5323.164
403.5619.983
50
2.93
17.595
n
R
A
219.2315.291
317.2423.182
415.6227.575
514.2830.073
613.1531.461
712.1932.165
811.3532.435
910.6332.421
109.9932.219
206.2427.476
304.5323.164
403.5619.983
50
2.93
17.595

NOTE.—In this calculation the reads are assumed to sequence 600 bases per sample, CL, CS, and CR are, respectively, assumed to be 40, 0.10, and 6, and Θ = 0.003.

Open in new tab
Table 2

Numbers of Unlinked Loci and Reads (R) and Accuracy Achieved (A) for Different Sample Sizes When Costs Total US$ 1000

n
R
A
219.2315.291
317.2423.182
415.6227.575
514.2830.073
613.1531.461
712.1932.165
811.3532.435
910.6332.421
109.9932.219
206.2427.476
304.5323.164
403.5619.983
50
2.93
17.595
n
R
A
219.2315.291
317.2423.182
415.6227.575
514.2830.073
613.1531.461
712.1932.165
811.3532.435
910.6332.421
109.9932.219
206.2427.476
304.5323.164
403.5619.983
50
2.93
17.595

NOTE.—In this calculation the reads are assumed to sequence 600 bases per sample, CL, CS, and CR are, respectively, assumed to be 40, 0.10, and 6, and Θ = 0.003.

Open in new tab

They show that the optimum accuracy is achieved with n = 8 and R near 11. Note that if a sample size of 50 is used, there is not enough money for three loci and only a bit more than half as much accuracy is achieved. It is much better to use multiple unlinked loci with smaller population samples.

This has assumed that the costs of sampling a new individual are very small. If instead they are, say CS = 10, then the table 2 becomes instead table 3.

Table 3

Numbers of Unlinked Loci and Reads (R) and Accuracy Achieved (A) for Different Sample Sizes When Costs Total US$ 1000

n
R
A
218.8514.988
316.7222.494
415.0026.482
513.5728.583
612.3729.591
711.3429.935
810.4529.864
99.6829.529
109.0029.027
205.0022.024
303.1816.264
402.1412.038
50
1.47
8.841
n
R
A
218.8514.988
316.7222.494
415.0026.482
513.5728.583
612.3729.591
711.3429.935
810.4529.864
99.6829.529
109.0029.027
205.0022.024
303.1816.264
402.1412.038
50
1.47
8.841

NOTE.—In this calculation the reads are assumed to sequence 600 bases per sample, CL, CS, and CR are, respectively, assumed to be 40, 10, and 6 and Θ = 0.003.

Open in new tab
Table 3

Numbers of Unlinked Loci and Reads (R) and Accuracy Achieved (A) for Different Sample Sizes When Costs Total US$ 1000

n
R
A
218.8514.988
316.7222.494
415.0026.482
513.5728.583
612.3729.591
711.3429.935
810.4529.864
99.6829.529
109.0029.027
205.0022.024
303.1816.264
402.1412.038
50
1.47
8.841
n
R
A
218.8514.988
316.7222.494
415.0026.482
513.5728.583
612.3729.591
711.3429.935
810.4529.864
99.6829.529
109.0029.027
205.0022.024
303.1816.264
402.1412.038
50
1.47
8.841

NOTE.—In this calculation the reads are assumed to sequence 600 bases per sample, CL, CS, and CR are, respectively, assumed to be 40, 10, and 6 and Θ = 0.003.

Open in new tab
Table 4

Sample Size, Number of Bases Which can be Sequenced at a Single Locus with a Total of 10,000 Bases Sequenced and the Accuracy that Is Achieved (A) with a Cost-Per-Base Model Analogous to that of Pluzhnikov and Donnelly (1996)

n
s
A
25000.000.000091
33333.330.000157
42500.000.000197
52000.000.000220
61666.670.000231
71428.570.000236
81250.000.000236
91111.110.000234
101000.000.000230
11909.090.000226
12833.330.000221
20500.000.000183
30333.330.000149
40250.000.000126
50
200.00
0.000110
n
s
A
25000.000.000091
33333.330.000157
42500.000.000197
52000.000.000220
61666.670.000231
71428.570.000236
81250.000.000236
91111.110.000234
101000.000.000230
11909.090.000226
12833.330.000221
20500.000.000183
30333.330.000149
40250.000.000126
50
200.00
0.000110
Open in new tab
Table 4

Sample Size, Number of Bases Which can be Sequenced at a Single Locus with a Total of 10,000 Bases Sequenced and the Accuracy that Is Achieved (A) with a Cost-Per-Base Model Analogous to that of Pluzhnikov and Donnelly (1996)

n
s
A
25000.000.000091
33333.330.000157
42500.000.000197
52000.000.000220
61666.670.000231
71428.570.000236
81250.000.000236
91111.110.000234
101000.000.000230
11909.090.000226
12833.330.000221
20500.000.000183
30333.330.000149
40250.000.000126
50
200.00
0.000110
n
s
A
25000.000.000091
33333.330.000157
42500.000.000197
52000.000.000220
61666.670.000231
71428.570.000236
81250.000.000236
91111.110.000234
101000.000.000230
11909.090.000226
12833.330.000221
20500.000.000183
30333.330.000149
40250.000.000126
50
200.00
0.000110
Open in new tab

Again, the optimum is small, n = 7, having shrunk slightly with the higher costs of sampling. The optimum number of unlinked loci and reads is again R = 11. Once again, a higher sample size sacrifices much accuracy by forcing use of fewer unlinked loci. If the sample size is taken to be 50 instead, there is barely enough money to analyze the two loci, and the accuracy attained is not even one-third as great.

Calculations with a smaller value of Θ, 0.001, show that this favors slightly smaller sample sizes and more loci. These show the surprising effectiveness of a many-locus, few-individuals strategy.

If only integer numbers of reads are allowed and we wish not to exceed the cost target, R must be rounded downward from the value in equation (15) before being used in equation (16). The effect is to alter the optimal sample sizes only slightly (the optimal values of being 7 in both cases, with a small reduction in accuracy per unit cost).

Comparison with Pluzhnikov and Donnelly

We may compare the results with those in the pioneering work by Pluzhnikov and Donnelly (1996). They used the estimators of Watterson (1975) and Tajima (1983) and considered both recombining and nonrecombining sequences. The present study ignores recombination, though it does use a more powerful estimation method for Θ. Pluzhnikov and Donnelly (1996) also used a more restricted model of costs. In effect, their model has CL = 0 and CS = 0. It also takes the cost of sequencing to be a cost-per-base sequenced, equivalent to our first model. We can make the analysis correspond closely to the central column of results in their figure 3 by using the cost-per-base model, with C = 10,000, Θ = 0.001 (their quantity Θ is our sΘ, their L is in this no-recombination case our s), L = 1, and CB = 1.

FIG. 3.—
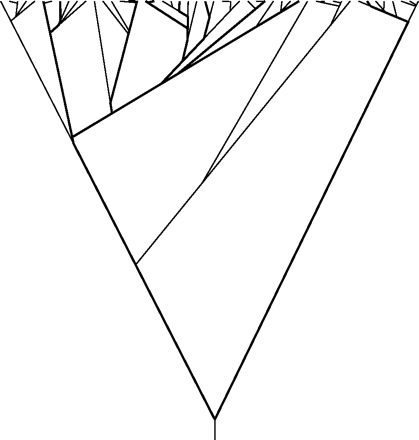
A simulated coalescent with 10 tips (dark lines) and with 40 more tips added.
Open in new tabDownload slide

A simulated coalescent with 10 tips (dark lines) and with 40 more tips added.

In this case, the total cost of the study will be LsnCB, which is fixed at 10,000. Therefore, maximizing the accuracy per base (eq. 11) will maximize the accuracy for this fixed cost. For each sample size n, we must use s = 10,000/n. Substituting this into equation (11), we can evaluate Q for each n (see fig. 4).

The optimum sample size n = 8, essentially the same value found by Pluzhnikov and Donnelly (1996). They measured the squared coefficient of variation, which would in this case be the inverse of 10,000Q. The accuracy values implied by these values show a curve similar to ours, except that as they use less powerful estimators of Θ they achieve about three-fourths of the accuracy we do.

Thus, our results validate a central conclusion of their paper—that it is optimal to take small samples of organisms from populations. Figure 3 shows a simulated coalescent tree. The tree connecting 10 randomly chosen tips is shown by darker lines.

Adding 40 more tips, we add the thinner lines. Note that much of the length of the tree is known once 10 tips have been sampled. The 40 additional tips add a minority of the length. Many of the 40 additional sequences are near duplicates of the first 10 sequences.

Other Parameters

Both the papers of Pluzhnikov and Donnelly (1996) and this one have concentrated on the estimation of Θ. In more complex cases, we may well be interested in estimating the migration rates, population growth rates, or recombination rates. The paper of Pluzhnikov and Donnelly (1996) contains evidence that the presence of other parameters will also change the conclusions about estimating Θ. They find that as the sequence length is increased in the presence of recombination, the accuracy of estimates of Θ increases, as one is examining regions that have different coalescents. Both the present paper and theirs show that when there is no recombination, extending sequence length does not increase accuracy of estimation of Θ.

Other Parameters

There is no reason to believe that the optimal sample design will be the same for all parameters that might be estimated. Here are some guesses as to how the conclusions would change in other cases. In particular, likelihood methods are available to infer parameters in cases with exponential population growth (Griffiths and Tavaré 1994a; Kuhner, Yamato, and Felsentein 1998), cases with recombination (Griffiths and Marjoram 1996; Kuhner, Yamato, and Felsentein 2000), and cases with migration (Beerli and Felsenstein 1999, 2001; Bahlo and Griffiths 2000).

Recombination

If we allow recombination and estimate both Θ and the scaled recombination rate per site r/μ, it seems likely that we need long sequences to do a good job of estimating the recombination rate because the opportunity for detecting recombination increases with sequence length. To the extent that the objective is to maximize the accuracy per unit cost in estimating r/μ, one would want longer sequences and fewer loci.

Population Growth

If the population were growing exponentially and a scaled growth rate such as g/μ was estimated, one could do a good job of estimating this parameter only by sampling enough loci that the rate of coalescence could be inferred far enough back in time. This would place a premium on having more loci and thus smaller population sample sizes.

Migration

When migration is allowed and migration rates of the form mij/μ are inferred, longer sequences will help make an accurate estimate of the individual coalescent trees and thus place past migration events more accurately. This would suggest a shift in the trade-offs toward longer sequences, with correspondingly fewer loci. If the migration rates were high, migration events deep in the coalescent tree would be less visible. To infer migration rates and patterns, one would then want to have larger sample sizes in each population to detect recent migrations.

All of these are speculations; these issues need intensive study by simulation and the development of adequate approximations to the variance of the estimators.

Watterson's Estimator

In all computer simulations, Watterson's (1975) number of segregating sites estimator of Θ was also obtained. We are therefore in a position to empirically assess its effectiveness as an estimator of Θ. Fu and Li (1993) used the variance formulas in Watterson's original paper to evaluate the efficiency of the number of segregating sites estimator. In our terms, this result is
\[E_{w}{=}\frac{{\sum}_{k{=}2}^{n}\frac{1}{(1{+}\frac{k{-}1}{s{\Theta}})}}{{\sum}_{k{=}2}^{n}/\left({\sum}_{k{=}2}^{n}\frac{1}{k}\right)^{2}{+}\frac{1}{s{\Theta}{\sum}_{k{=}2}^{n}\frac{1}{k}}}.\]
(17)
The approximation formula (9) can also be used but is rather too rough for this comparison—the upper and lower bounds give noticeably different answers unless the number of sites is large.

The approximation formula (17) relies on Fu and Li's approximation and also assumes that Watterson's variance formula is exactly correct. It is correct for the infinite-sites model, but we are dealing here with a finite-sites model. Watterson's estimator may be somewhat biased, and the variance formula may be at least slightly incorrect.

Bias

In the infinite-sites model, the Watterson estimator of Θ can be proven to be unbiased. For the finite-sites model used here, it would generally be expected to be biased downward because a further mutation could remove a site from consideration as a segregating site. With Θ = 0.003, the mean Watterson estimates of Θ ranged, over the 15 cases, from 0.00281320 to 0.00320929, with their mean being 0.0029588, 1.37% low. Of these, 5 of the 15 cases were above the true Θ. This is less bias than was seen in the MCMC estimates. In the case where Θ = 0.01, the mean Watterson estimates for the 15 cases ranged from 0.00926154 to 0.01002751, with their mean being 0.00958219, 4.2% low. Only one case was above the true value 0.01. This may be the downward bias that is expected owing to multiple mutations at a site.

Variance

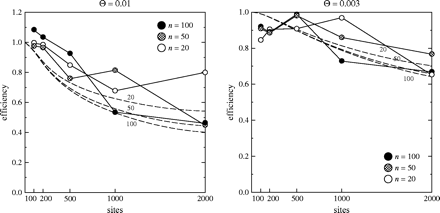
We can extract empirical variances of the Watterson estimates from our simulation. In this case there is no variance component for runs, so that we do not need to concern ourselves with extrapolating what would happen with infinitely long runs of the program. The general conclusion (from fig. 4) is that the approximation in equation (9) is good, though there is some sign that the efficiency of Watterson's estimator exceeds the approximation. A reviewer of this paper has pointed out that the approximation formula reflects the fact that the behavior of Watterson's estimator under the infinite-sites model depends on s and Θ only through their product, which is twice the expected number of mutations in the whole population per sequence (this is conventionally called θ in population genetics). The efficiency of Watterson's estimator is reasonably high, but declines markedly as θ exceeds 5, which is a larger value of θ than is usually biologically reasonable. The coalescent likelihood estimators can then extract noticeably more information from the data.

FIG. 4.—
An approximation to the efficiency (eq. 17 as curves) of the Watterson estimator of Θ, together with simulation values (as points), for the two values of Θ. Note the different vertical scales for the two graphs.
Open in new tabDownload slide

An approximation to the efficiency (eq. 17 as curves) of the Watterson estimator of Θ, together with simulation values (as points), for the two values of Θ. Note the different vertical scales for the two graphs.

Lauren McIntyre, Associate Editor

I wish to thank Mary Kuhner, Peter Beerli, and Jon Yamato for important help and advice; Peter Donnelly and Anna Pluzhnikov for discussing their work; Allison Shaw for helpful programming; and Stanley Sawyer, Scott Edwards, and anonymous reviewers for helpful comments on the manuscript. One of the reviewers pointed out to me that the approximation formulas for accuracy of coalescent estimates depended on s and Θ only through their product, θ. I also wish to thank Sam Wasser, Carol Sibley, Bob Braun, and Jim Thomas for discussing sequencing costs with me. Matt Carling and Robb Brumfield generously showed me the results of their own as-yet-unpublished simulation study on the effect of different number of loci. This work has been supported by National Institutes of Health grants no. R01 GM51929 and R01 GM071639 and by National Science Foundation grants no. BIR-9527687 and DEB-9815650.

References

Bahlo, M., and R. C. Griffiths.

2000
. Inference from gene trees in a subdivided population.
Theor. Popul. Biol.
57
:
79
–95.

Beerli, P., and J. Felsenstein.

1999
. Maximum-likelihood estimation of migration rates and effective population numbers in two populations using a coalescent approach.
Genetics
152
:
763
–773.

———.

2001
. Maximum likelihood estimation of a migration matrix and effective population sizes in n subpopulations by using a coalescent approach.
Proc. Natl. Acad. Sci. USA
98
:
4563
–4568.

Edwards, A. W. F.

1970
. Estimation of the branch points of a branching diffusion process.
J. R. Stat. Soc. B
32
:
155
–174.

Felsenstein, J.

1988
. Phylogenies from molecular sequences: inference and reliability.
Annu. Rev. Genet.
22
:
521
–565.

———.

1992
a. Estimating effective population size from samples of sequences: inefficiency of pairwise and segregating sites as compared to phylogenetic estimates.
Genet. Res.
59
:
139
–147.

———.

1992
b. Estimating effective population size from samples of sequences: a bootstrap Monte Carlo approach.
Genet. Res.
60
:
209
–220.

Fu, Y.-X.

1994
. A phylogenetic estimator of effective population size or mutation rate.
Genetics
136
:
685
–692.

Fu, Y.-X., and W.-H. Li.

1993
. Statistical tests of neutrality of mutations.
Genetics
133
:
693
–709.

Griffiths, R. C.

1989
. Genealogical tree probabilities in the infinitely-many-site model.
J. Math. Biol.
27
:
667
–680.

Griffiths, R. C., and P. Marjoram.

1996
. Ancestral inferences from samples of DNA sequences with recombination.
J. Comput. Biol.
3
:
479
–502.

Griffiths, R. C., and S. Tavaré.

1994
a. Sampling theory for neutral alleles in a varying environment. Philos.
Trans. R. Soc. Lond. Ser. B Biol. Sci.
344
:
403
–410.

———.

1994
b. Ancestral inference in population genetics.
Stat. Sci.
9
:
307
–319.

Kingman, J. F. C.

1982
a. The coalescent.
Stoch. Proc. Appl.
13
:
235
–248.

———.

1982
b. On the genealogy of large populations.
J. Appl. Prob.
19A
:
27
–43.

———.

1982
c. Exchangeability and the evolution of large populations. Pp. 97–112 in G. Koch and F. Spizzichino, eds. Exchangeability in probability and statistics. Proceedings of the International Conference on Exchangeability in Probability and Statistics, Rome, 6th–9th April, 1981, in honour of Professor Bruno de Finetti. North-Holland/Elsevier, Amsterdam.

Kuhner, M. K., J. Yamato, and J. Felsenstein.

1995
. Estimating effective population size and mutation rate from sequence data using Metropolis-Hastings sampling.
Genetics
140
:
1421
–1430.

———.

1997
. Applications of Metropolis-Hastings genealogy sampling. Pp. 183–192 in P. Donnelly and S. Tavare, eds. Progress in population genetics and human evolution. IMA volumes in mathematics and its applications, Vol. 87. Springer Verlag, Berlin, Germany.

———.

1998
. Maximum likelihood estimation of population growth rates based on the coalescent.
Genetics
149
:
429
–434.

———.

2000
. Maximum likelihood estimation of recombination rates from population data.
Genetics
156
:
1393
–1401.

Pluzhnikov, A., and P. Donnelly.

1996
. Optimal sequencing strategies for surveying molecular genetic diversity.
Genetics
144
:
1247
–1262.

Tajima, F.

1983
. Evolutionary relationships of DNA sequences in finite populations.
Genetics
105
:
437
–460.

Watterson, G. A.

1975
. On the number of segregating sites in genetical models without recombination.
Theor. Popul. Biol.
7
:
256
–276.

Wilson, I. R., G. Weale, and D. G. Balding.

2003
. Inferences from DNA data: population histories, evolutionary processes, and forensic match probabilities.
J. R. Stat. Soc. Ser. A
166
:
155
–188.

© The Author 2005. Published by Oxford University Press on behalf of the Society for Molecular Biology and Evolution. All rights reserved. For permissions, please e-mail: journals.permissions@oxfordjournals.org
Issue Section:
research articles
Download all slides