Abstract
Blindness has evolved repeatedly in cave-dwelling organisms, and investigating loss of sight presents an opportunity to understand the operation of fundamental evolutionary processes, including drift, selection, mutation, and migration. The observation of blind organisms has prompted many theories for their blindness, including loss-by-disuse and selection against eye development when eyes are not used. Here we have developed a model that shows just how strong selection must be for blind populations of a cave-dwelling species to evolve. We used approximations to determine levels of selection that would result in caves containing only sighted individuals, only blind individuals, or a stable population of both. We then incorporated drift into the model using simulations. Based on our model, strong selection is necessary for the evolution of blindness unless immigration rates are extremely low. Drift decreased the fixation of blindness in populations, although for intermediate levels of migration the level of selection required to fix blindness decreased substantially. We hypothesize that this degree of selection may be due to phototaxis in sighted individuals, who move toward the light leaving only blind individuals in the cave.
Introduction
Blindness has evolved repeatedly across taxa in caves, creating nearly a thousand cave-dwelling species and many more populations (Culver et al., 2000; Dowling et al., 2002; Bradic et al., 2012; Coghill et al., 2014). However, many populations of blind individuals experience some level of immigration, which would be expected to prevent the fixation of blindness in a newly established population (Avise and Selander, 1972; Bradic et al., 2012; Coghill et al., 2014). Thus, blind cave-dwelling populations of typically sighted species pose an interesting challenge to our understanding of evolutionary biology. Namely, how does a fixed phenotype evolve from low frequency despite immigration?
Darwin suggested that eyes would be lost by “disuse” (Darwin, 1859). We now consider this hypothesis the “neutral mutation hypothesis” — random mutations can accumulate in eye related genes or regulatory regions when, as in caves, there is no purifying selection to eliminate them. However, the accumulation of mutations (mutation pressure) causing blindness would take a long time to result in fixation of blindness in populations on its own (Barr, 1968). Thus, it is genetic drift combined with mutation pressure that would lead to blindness (Kimura and King, 1979; Borowsky, 2015). Genetic drift is the increases the frequency of blindness alleles created by mutations: eyes become increasingly less functional and finally disappear completely (Wilkens, 1988).
There are a variety of cave dwelling vertebrates and invertebrates (referred to as cavernicoles, troglophiles, and troglobites). However, much of the work on the evolution of blindness has focused on the blind form of cavefishes, e.g. the Mexican tetra (Astyanax mexicanus) and Atlantic molly (Poecilia mexicana). For example, the hypothesis of relaxed selection is supported by the observation of a high number of mutations in cavefish putative eye genes (Hinaux et al.,2013; Protas et al., 2006; Gross et al., 2009). However, developmental evidence does not support this hypothesis: cavefish embryos begin eye development, but the eye disappears in larvae (Langecker et al., 1993; Jeffery et al., 2003). Random mutations should occur in genes controlling early eye development as well. Furthermore, although drift would often lead to loss of seeing individuals joining a population of blind individuals, this model depends on developing a high frequency of blindness in a cave population simply by drift in isolation.
Alternatively, the “adaptation hypothesis” suggests that there is a cost to an eye; thus, individuals without eyes have greater fitness resulting in the eventual elimination of seeing individuals. This cost may either come from the energy required to develop a complex structure or due to the vulnerability of the eye (Barr, 1968; Strickler et al., 2007; Jeffery, 2005; Protas et al., 2007; Niven, 2008; Niven and Laughlin, 2008; Moran et al., 2015). Another hypothesis states that sight is not lost not due to the “cost” of development but due to pleiotropic mutations selected for other traits. For example, in Mexican tetra increased expression of Hedgehog (Hh; Jeffery, 2005) likely affects feeding structures, allowing better foraging in low light conditions (Jeffery, 2005, 2001). However, increased Hh signaling inhibits pax6 expression, which results in eye loss during development (Jeffery, 2005; Yamamoto et al., 2004). Alternatively, cryptic variation may be maintained in normal conditions, and expressed as blindness only in case of stress, such as entry into the cave (Rohner et al., 2013). When the cryptic variation is “unmasked” it is then exposed to selection and could become fixed in the population.
These mechanisms of selection would result in the evolution of a blind population occurring quite slowly. Furthermore, given that there is often migration from surface to cave populations and that and these populations can interbreed, it seems that blind phenotypes should be lost (Avise and Selander, 1972). One possibility is that the strength of selection for blindness is large enough to counter immigration (Avise and Selander, 1972). Although blind fish maintained in the dark in the lab do not appear to have an advantage of this magnitude (Sadoglu, 1967), recent work suggests a very high cost to developing neural tissue, including eyes (Moran et al., 2015).
Due to the immigration of individuals from the surface and the expected level of selection for the eyeless phenotype, cave populations are an example of migration–selection balance (Wright, 1969; Hedrick, 2011; Nagylaki, 1992). However, much of the work in this area has explored the “invasion” of a novel allele or the maintenance of polymorphism, rather than fixation of different alleles in different populations (Yeaman and Otto, 2011; Yeaman and Whitlock, 2011).
Here we have developed a model that shows just how strong selection must be to generate blind populations of a cave-dwelling species. Incorporating genetic drift into the model actually increases the level of selection required for fixation. This level of selection is not compatible with the hypothesis that eyes are lost due to drift or that eyes are lost due to selection for improved foraging and pleiotropy (assuming pleiotropy imposes only weak selection). However, if eye development imposes a high cost (Moran et al., 2015) then the adaptation hypothesis is plausible. Alternatively, we suggest reconsidering the historic hypothesis that a high level of selection is due to migration of seeing individuals, who are strongly phototactic, out of the cave (Lankester, 1925; Romero, 1985). Thus, we suggest that a standing presence of blindness alleles, combined with extreme loss of sighted individuals in the cave, is a likely scenario leading to evolution of blind cave-dwelling populations.
Model and Analysis
Assumptions
Consider a species with two populations: surface-dwelling and cave-dwelling. We are interested in determining when the cave population will evolve blindness, i.e. become comprised of mostly blind individuals, as has occurred in numerous natural systems. We first assume that the surface and cave populations do not experience drift (i.e. populations are of infinite size). Additionally, immigration from the surface population into the cave affects the allele frequency in the cave, but emigration from the cave to the surface does not affect the surface population, as we assume that the surface population is significantly larger than the cave. Generations are discrete and non-overlapping, and mating is random. We track a single biallelic locus, where b+ is the dominant, seeing allele, and where b− is the recessive, blindness allele. The frequencies of b− are denoted by  on the surface and q ∈ [0, 1] in the cave. On the surface, we assume that blindness is selected against, and
on the surface and q ∈ [0, 1] in the cave. On the surface, we assume that blindness is selected against, and  is dictated by mutation-selection balance.
is dictated by mutation-selection balance.
Calculating the frequency of the blindness allele
Within the cave, the life cycle is as follows. (1) Embryos become juveniles and experience constant selection with relative fitnesses of  and
and  where s ≥ 0. (2) Juveniles migrate into and out of the cave such that a fraction m of adults come from the surface and 1 − m from the cave, where 0 ≤ m ≤ 1. (3) Adults generate gametes with one-way mutation, where 0 ≤ u ≤ 1 is the probability that a b+ becomes a non-functional b−. (4) Gametes unite randomly to produce embryos. Given this life cycle, we calculate the allele frequency of the daughter generation (q′) via standard equations:
where s ≥ 0. (2) Juveniles migrate into and out of the cave such that a fraction m of adults come from the surface and 1 − m from the cave, where 0 ≤ m ≤ 1. (3) Adults generate gametes with one-way mutation, where 0 ≤ u ≤ 1 is the probability that a b+ becomes a non-functional b−. (4) Gametes unite randomly to produce embryos. Given this life cycle, we calculate the allele frequency of the daughter generation (q′) via standard equations:



The change in allele frequency in one generation is

Furthermore, b− is maintained at a stable equilibrium on the surface:  , where z is the selection coefficient against b− on the surface and u ≤ z ≤ 1.
, where z is the selection coefficient against b− on the surface and u ≤ z ≤ 1.
Identifying equilibrium frequencies of the blindness allele
The model we have developed is an example of migration-selection balance (Figure 1; Wright, 1969; Hedrick, 2011; Nagylaki, 1992). An equilibrium exists for this model when Δq = 0. Assuming s > 0 and setting Δq = 0, Equation 2 can be rearranged into the following cubic polynomial
 where
where

Dynamics of cave populations are governed by migration-selection balance. The top curve shows the change in allele frequency due to selection, while the bottom curve shows the change in allele frequency due to immigration. The middle curve shows how selection and migration are balanced to produced three equilibria points. Parameters: s = 0.1, m = 0.01, u = 10−6,  .
.
There are three possible roots of this equation, corresponding to three possible equilibria. Depending on the parameter values, Equation 3 may have three real roots or one real root and two imaginary roots. While the values of the roots of this polynomial can be expressed analytically, these equations are too complex to be helpful for understanding the system. For simplicity, we will let  represent any possible equilibrium, and
represent any possible equilibrium, and  , stand for the roots of Equation 3.
, stand for the roots of Equation 3.
Rather than tackling the equilibria directly, we first demonstrate that the cave has a protected polymorphism. A protected polymorphism exists if the allele frequency moves away from both fixation and extinction, i.e. Δq < 0 for q = 1 and Δq > 0 for q = 0. For q = 0
 and q = 0 will be an equilibrium if u = 0; otherwise Δq > 0 at q = 0 due to immigration of individuals containing b− (Figure 2). For q = 1
and q = 0 will be an equilibrium if u = 0; otherwise Δq > 0 at q = 0 due to immigration of individuals containing b− (Figure 2). For q = 1
 and q = 1 will be an equilibrium if m = 0 or u = 1; otherwise Δq < 0 at q = 1 due to immigration of individuals containing b+ (Figure 2). Thus a protected polymorphism always exists except at the edge cases m = 0, u = 0, and u = 1. In biological terms, the cave population will be polymorphic despite directional selection for b− if there is some immigration from the surface population and the surface population is polymorphic. For s = 0, there is only one equilibrium, and it is near 0. For large s, there is only one equilibrium, and it is near 1. Three equilibria will only exist for moderate levels of selection (Figure 2).
and q = 1 will be an equilibrium if m = 0 or u = 1; otherwise Δq < 0 at q = 1 due to immigration of individuals containing b+ (Figure 2). Thus a protected polymorphism always exists except at the edge cases m = 0, u = 0, and u = 1. In biological terms, the cave population will be polymorphic despite directional selection for b− if there is some immigration from the surface population and the surface population is polymorphic. For s = 0, there is only one equilibrium, and it is near 0. For large s, there is only one equilibrium, and it is near 1. Three equilibria will only exist for moderate levels of selection (Figure 2).
As selection increases, the evolutionary dynamics of the cave population changes. When s is low (bottom line; s = 0), there is only one equilibrium: near 0. As s increases (middle five lines, s = 0.05, 0.1, 0.15, 0.2, and 0.25) the local maximum (upper hump) increases and crosses the x-axis, producing three equilibria. When s gets high enough (top line; s = 0.3), the local minimum (lower valley) also crosses the x-axis, resulting in one equilibrium again. For all curves m = 0.01, u = 10−6, and  . The figure on the right is an enlarged view of the box in the figure on the left.
. The figure on the right is an enlarged view of the box in the figure on the left.
Validity of equilibria. An equilibrium is only valid in our model if it is real and between [0, 1]; otherwise, it is not biologically interpretable in this system. The lower bound for any equilibrium is  if m > 0 or u > 0; otherwise it is 0 (Lemma 1). The upper bound for any equilibrium is
if m > 0 or u > 0; otherwise it is 0 (Lemma 1). The upper bound for any equilibrium is  (Lemma 2). Thus if any equilibrium is real it is valid. The only exception to this rule is the edge case when s = m = u = 0. In this case, all evolutionary forces are eliminated, and q′ = q for all q. Here every possible value of q is an equilibrium, although only q ∈ [0, 1] makes any sense. Furthermore, it is important to note that if m > 0,
(Lemma 2). Thus if any equilibrium is real it is valid. The only exception to this rule is the edge case when s = m = u = 0. In this case, all evolutionary forces are eliminated, and q′ = q for all q. Here every possible value of q is an equilibrium, although only q ∈ [0, 1] makes any sense. Furthermore, it is important to note that if m > 0,
 indicating that the equilibrium frequencies in the cave are always greater than the allele frequency on the surface.
indicating that the equilibrium frequencies in the cave are always greater than the allele frequency on the surface.
Approximations. In orderto study equilibria, we will simplify our model by assuming that u ≪ 1 such that 1 − u ≈ 1 and

Weak-selection approximation. If selection is weak, then an equilibrium exists near  (Figure 2). We use a second-order Taylor series at q = 0 to determine the upper bound on s for the presence of three equilibria (i.e. when selection is so strong that an equilibrium near
(Figure 2). We use a second-order Taylor series at q = 0 to determine the upper bound on s for the presence of three equilibria (i.e. when selection is so strong that an equilibrium near  does not exist). The second-order series allows us to determine the lower two equilibrium points, although this approximation is inaccurate as q increases. This approximation gives us
does not exist). The second-order series allows us to determine the lower two equilibrium points, although this approximation is inaccurate as q increases. This approximation gives us
 after assuming that
after assuming that  . This equation has two roots, which are the lowest two of three total equilibria,
. This equation has two roots, which are the lowest two of three total equilibria,

These two roots exist only if
 which provides us with an estimate of the upper bound on s for the presence of three equilibria.
which provides us with an estimate of the upper bound on s for the presence of three equilibria.
The derivative of Equation 6 is  , and a equilibrium will be stable if
, and a equilibrium will be stable if  . From this, it can be easily shown that
. From this, it can be easily shown that  is stable and
is stable and  is unstable.
is unstable.
Strong-selection approximation. In order to determine the lower bound on s for the presence of three equilibria, we assume that selection is strong enough such that u/s ≈ 0 and  . Therefore,
. Therefore,
 and the equilibria can be described as
and the equilibria can be described as

The latter two equilibria will exist only if
 which provides us an estimate of the lower bound for the presence of three equilibria.
which provides us an estimate of the lower bound for the presence of three equilibria.
The derivative of Equation 8 is  , and it can be easily shown that
, and it can be easily shown that  is unstable and
is unstable and  is stable.
is stable.
Validity of approximations. Bysubstituting  and
and  back into Equation 5, we obtain
back into Equation 5, we obtain  . Thus, Δq ≤ 0, which indicates that
. Thus, Δq ≤ 0, which indicates that  overestimates
overestimates  and that
and that  underestimates
underestimates  . Bysubstituting
. Bysubstituting  and
and  back into Equation 5, we find that
back into Equation 5, we find that  . Thus Δq ≥ 0, which indicates that
. Thus Δq ≥ 0, which indicates that  overestimates
overestimates  and that
and that  underestimates
underestimates  . However, the error in our approximations is slight (Figure 3).
. However, the error in our approximations is slight (Figure 3).
Our equilibria approximations are accurate. The approximations developed in this paper (solid lines) are a good fit for calculated values of s that result in equilibrium for a given q (circles) using Equation 3. Because these approximations are accurate we can use them to better understand this system. The dashed lines are our approximate bounds for the existence of three equilibria (i.e. for small and large values of s, there is one value of q; for intermediate values of s there are three possible values of q). Other parameters are m = 0.01, u = 10−6, and  .
.
Dynamics. The dynamics of the evolution of the cave population depend on the parameter values and the starting allele frequency, q0 (Table 1). If there is one equilibrium value, then b− will evolve to be the major allele in the population if  . If there are three equilibria, and
. If there are three equilibria, and  , then b− will become the major allele only if its initial frequency is above the threshold
, then b− will become the major allele only if its initial frequency is above the threshold  .
.
Evolutionary Dynamics of Blindness as t → ∞
Based on these approximations the dynamics of the system can be summarized as follows. First, there are three possible equilibria:  , and
, and  . Second, there are four possible equilibria configurations: 1, 2a, 2b, and 2c.
. Second, there are four possible equilibria configurations: 1, 2a, 2b, and 2c.
Case 1,  : only one equilibrium exists, and it is stable. The population will always evolve towards it.
: only one equilibrium exists, and it is stable. The population will always evolve towards it.
Case 2,  : depending on the strength of s, this case may have one of three possible configurations:
: depending on the strength of s, this case may have one of three possible configurations:
Case 2a,  : Only one equilibrium exists,
: Only one equilibrium exists,  , and it is stable. The population will always evolve towards it.
, and it is stable. The population will always evolve towards it.
Case 2b,  : All three equilibria exist;
: All three equilibria exist;  and
and  are stable, while
are stable, while  is unstable. If the population starts below
is unstable. If the population starts below  , it will evolve towards
, it will evolve towards  . If it starts above
. If it starts above  , it will evolve towards
, it will evolve towards  .
.
Case 2c,  : only one equilibrium,
: only one equilibrium,  , exists, and it is stable. The population will always evolve towards it.
, exists, and it is stable. The population will always evolve towards it.
The evolution of blindness
When the cave population is founded, its initial allele frequency will likely match the equilibrium frequency on the surface  . Since
. Since  , the allele frequency in the cave will increase due to selection until it reaches the lowest equilibrium. If this equilibrium is
, the allele frequency in the cave will increase due to selection until it reaches the lowest equilibrium. If this equilibrium is  , we consider the population to have evolved blindness. If there is only a single equilibrium, and
, we consider the population to have evolved blindness. If there is only a single equilibrium, and  (i.e.
(i.e.  , Lemma 3), b− will evolve to become the major allele. If there are three equilibria (Case 2b), then the population will not evolve blindness: the maximum value of
, Lemma 3), b− will evolve to become the major allele. If there are three equilibria (Case 2b), then the population will not evolve blindness: the maximum value of  . Therefore, blindness will only evolve if
. Therefore, blindness will only evolve if

This approximation is valid when  and u ≪ m ≪ 1. We analytically calculated ultimate allele frequencies for our model and compared it to the above approximation (Figure 4A), and we also explored the approximation when u and
and u ≪ m ≪ 1. We analytically calculated ultimate allele frequencies for our model and compared it to the above approximation (Figure 4A), and we also explored the approximation when u and  are varied (Figure 5).
are varied (Figure 5).
Populations evolve blindness with the help of strong selection. (A) The equilibrium b− frequency for an infinite population and (B–D) average frequencies after t generations in finite populations (100 replicates). Colors correspond to the frequency of b− for a given combination of s and m, where blue is high (blindness evolved) and red is low (blindness did not evolve). Colors levels are determined by a base-10 logit scale. The solid white line corresponds to the threshold calculated in Equation 9, and the dash white line corresponds to  (Equation 11). The area between the solid and dashed lines corresponds to the region where three equilibria exist. Other parameters are u = 10−6,
(Equation 11). The area between the solid and dashed lines corresponds to the region where three equilibria exist. Other parameters are u = 10−6,  , and
, and  .
.
Strong selection is necessary for the evolution of blindness. Each panel represents a different mutation rate, and each line represents a threshold for the evolution of blindness based on  and
and  . The rate of mutation of b+ to b− alleles is a significant factor in the establishment of the thresholds, e.g. if
. The rate of mutation of b+ to b− alleles is a significant factor in the establishment of the thresholds, e.g. if  and m = 0.01, then s > 0.129 for u = 10−4 and s > 0.250 for u = 10−6; if m = 0.001, then s > 0.004 for u = 10−4 and s > 0.023 for u = 10−6.
and m = 0.01, then s > 0.129 for u = 10−4 and s > 0.250 for u = 10−6; if m = 0.001, then s > 0.004 for u = 10−4 and s > 0.023 for u = 10−6.
Finite-population simulations
Constant migration
To investigate the impact of drift on our model, we simulated diploid populations of size N = 1000, where the frequency of adults was determined by drawing 2N alleles from a binomial distribution with mean qa (Equation 1b). q′ was calculated based on the post-drift adult allele frequency and immigration. For each set of parameters, we recorded the average q′ frequency across these 100 populations at specific time points.
For high migration rates, the average allele frequency is similar to the infinite model, except that drift allows some populations that have three equilibria to evolve blindness (Figure 4B). However, at low migration rates  , populations have low average frequency of b− at 10 thousand generations, unless s > 1. As immigration decreased, these populations became dependent on de novo mutations to produce b−, which is a slow process. At 5 million generations, which is close to the estimated age of cavefish populations Gross (2012), the average allele frequency is a better match to the results from the the infinite-population model (Figure 4C); although, selection is ineffective for s < 1/2N = 5 × 10−4.
, populations have low average frequency of b− at 10 thousand generations, unless s > 1. As immigration decreased, these populations became dependent on de novo mutations to produce b−, which is a slow process. At 5 million generations, which is close to the estimated age of cavefish populations Gross (2012), the average allele frequency is a better match to the results from the the infinite-population model (Figure 4C); although, selection is ineffective for s < 1/2N = 5 × 10−4.
Episodic migration
Because cave and surface populations are may be connected intermittently due to flooding, we simulated periods of immigration followed by periods of isolation following a first-order Markov process. The probability of switching between isolation and immigration or vice versa was 10% every generation. Results for the intermittently connected simulations were nearly identical to previous simulations, with the exception that at high levels of migration and selection, drift was more effective in increasing allele frequencies (Figure 4D).
Discussion
Both our model and simulations show that strong selection (characterized as s > 0.05; Rieseberg and Burke, 2001) is necessary for a cave population to evolve blindness. Our simulations demonstrate that genetic drift, which is likely to occur in small cave populations, markedly decreases the fixation of these rare alleles, resulting in the need for even greater selection.
Model
Our model demonstrates that without drift, blindness occurs in cave populations only when s is large or m is very small. This result is logical: given low levels of immigration, selection increases the frequency of the blindness allele. In contrast, for high levels of immigration there will always be some sighted fish. This case essentially results in a single population, for which selection in the large surface population for sighted fish outweighs small-scale selection in the cave (Nagylaki and Lou, 2008). In other words, gene flow prevents local adaptation, as expected. For intermediate levels of immigration, there will be sighted fish unless selection removes them.
What is surprising about our result is the level of selection required to fix blindness in the population. This result contrasts with the level of the selection found in most cases of local adaptation. Sadoglu (1967) argued that given the observed number of populations of blind fish living in caves, drift would have fixed at least one for a useful eye, However, because all populations appear to be blind or with a significantly reduced eye, this indicates strong selection for “degenerative genes”.
Drift
The “neutral mutation hypothesis” is equivalent to no selection for the blindness allele in a small population. This hypothesis relies on drift to fix populations for blindness. Thus, we explored the interaction of immigration, selection and blindness with simulations. However, our simulations including drift produce similar results to our model, with two notable exceptions. First, as observed previously, drift removes the blindness allele when it occurs at low levels; thus, for low immigration rates, populations consisted primarily of sighted fish, except when very strong selection immediately increased the frequency of blindness. This is opposite of predicted by the “neutral mutation hypothesis”.
When migration is very high, drift has minimal effect, as the two populations essentially function as one, with the surface population swamping the smaller cave population. However, for intermediate levels of migration the level of selection required to fix blindness decreased substantially. In this case, immigration is increasing the frequency of the blindness allele in each generation, allowing more chances for selection to overcome drift. This result is consistent with the observation of Blanquart et al. (2012)
Allowing populations to evolve for longer periods of time does increase the likelihood that a population can drift to fixation for blindness. As for higher levels of immigration, more generations results in a greater chance for a blindness mutation to occur in the population, and for drift to increase the frequency of this allele. Similarly, increasing the mutation rate, either for the whole genome or as a way to allow multiple mutations to produce blindness, results in a greater likelihood of blind populations. As for higher levels of immigration, a greater chance of producing a mutation for blindness results in an increased number of chances for a population to evolve blindness.
Effect of intermittent connections
On the low end of migration, intermittent connections effectively result in a decrease in the immigration rate and “replenishment” of the blindness allele, which increases in the level of selection required to fix blindness in the population. In contrast, when immigration rates are high, disconnecting the two populations and effectively reducing the immigration rate allows populations to fix for blindness, at least until the next period of high immigration.
Previous observations of strong selection
The values we suggest here as “strong selection” are high, but not inconsistent with previous observations. Previous calculations of strong selection resulting in selective sweeps in wild populations range from 0.02–0.7 (Sáez et al., 2003; Schlenke and Begun, 2004; Wootton et al., 2002; Nair et al., 2003). Estimated selection coefficients for drug resistance in Plasmodium falciparum were 0.1–0.7 (Wootton et al., 2002; Nair et al., 2003). These extremely high values for selection led to fixation in 20–80 generations. For a major advantageous allele, the average value of s has been estimated as 0.11 in plants and 0.13 in animals (Rieseberg and Burke, 2001; Morjan and Rieseberg, 2004). Thus, estimated selection coefficients for cave species are consistent with a selection mechanism that is stronger than previously proposed.
Potential mechanisms of strong selection
Previous mechanisms of selection proposed for cave species have primarily been weak (Darwin, 1859; Sadoglu, 1967). However, recent work has suggested that eye development imposes a high metabolic cost, particularly for juveniles (Moran et al., 2015). In a food-limited environment, like a cave, this cost could lead to the level of selection suggested by our model. Additionally, an alternative mechanism of selection exists: migration of seeing individuals, who are strongly phototactic, out of the cave (Lankester, 1925; Romero, 1985). Emigration of sighted individuals functions like selection because it systematically removes b+ alleles from the cave population. Phototaxis has been observed in eyed cavefish (Espinasa and Borowsky, 2000). Migration thus imposes strong selection in the cave for blind individuals. This mechanism of strong selection would explain the observation that blindness in cave dwelling organisms evolved repeatedly. This hypothesis is consistent with all previous hypotheses of how blindness arises (i.e. random mutation or differential expression) but suggests an alternative mechanism of selection that is much stronger than previously proposed fitness advantages (i.e. reallocation of resources). Furthermore, it suggests a way of maintaining a mostly blind cave population despite interbreeding and gene flow from surface populations (Bradic et al., 2012; Avise and Selander, 1972). Interestingly, our work is consistent with work suggesting standing cryptic variation for eye size in cavefish (Rohner et al., 2013; Rohner, 2015). The primary effect of the variation being cryptic rather than de novo would be that the allele frequency in the surface population would be higher than expected. However, strong selection would still be required.
Alternatively, vibration attraction behavior, where individuals are attracted to moving objects, provides a strong advantage for some individuals by allowing them to find food (Yoshizawa et al., 2012). This behavior is observed in multiple cavefish populations (Yoshizawa et al., 2010). In contrast, this behavior would like result in predation in a sighted environment (Yoshizawa and Jeffery, 2011). Surface populations show a low frequency of this behavior (Yoshizawa and Jeffery, 2011). However, in this case the genetic basis of the behavior would have to be linked to blindness, and whether this is the case is unknown.
Application to other local adaptation scenarios
Although we have described our model in the context of cave and surface populations, with the allele under selection for blindness, this work also applies to other scenarios of local adaptation. Generally, our scenario can be considered a metapopulation with divergent selection (Blanquart et al., 2012; Yeaman and Otto, 2011). However, while previous work focused on stable polymorphism, here we have addressed how populations become fixed for a state.
Acknowledgments
This work was supported by Arizona State University’s School of Life Sciences and Barrett Honors College. Steven Wu, David Winter, and Kael Dai provided helpful feedback on this manuscript.
Appendix
If m >0 or u > 0. and s ≥ 0. the minimum value of an equilibrium is  . If m = u = 0 and s > 0, the minimum value of an equilibrium is 0. If m = u = s = 0, all points are equilibria, and thus 0 is the lowest possible valid equilibrium.
. If m = u = 0 and s > 0, the minimum value of an equilibrium is 0. If m = u = s = 0, all points are equilibria, and thus 0 is the lowest possible valid equilibrium.
Case 1. Let f(q) represent the change in allele frequency over one generation (Equation 2). Let  . if s = 0 and m > 0 (or u > 0), f (q*) = 0, and therefore q* is an equilibrium for these parameters.
. if s = 0 and m > 0 (or u > 0), f (q*) = 0, and therefore q* is an equilibrium for these parameters.
Now let s ≥ 0, and q < q*. The denominator of f(q) is positive, and the numerator is


Since f (q) > 0∀q < q*, q* is the lowest value that can be an equilibrium.
Case 2. Let m + u = 0 and s > 0. Now (10) is sq2(1 − q), which has its lowest equilibrium at 0.
Case 3. If s = 0, all possible values of q are equilibria. □
The maximum value of an equilibrium is  .
.
Let  . Since lims→∞f (q*) = 0, q* is a potential equilibrium. Now let q > q*.
. Since lims→∞f (q*) = 0, q* is a potential equilibrium. Now let q > q*.

Since f (q) < 0∀q > q*, q* is the highest value that can be an equilibrium.
If  and
and  , there exists an equilibrium ≥ 1/2.
, there exists an equilibrium ≥ 1/2.
By rearranging Equation 3, we find a formula for the migration rate that willgenerate an equilibrium at q:

First, we can show that  monotonically decreases for q ≥ 1/2:
monotonically decreases for q ≥ 1/2:
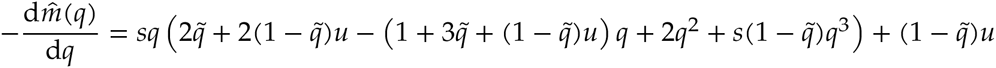
And

Therefore,  monotonically decreases from
monotonically decreases from  to
to  as q increases from 1/2 to 1. Stated another way, if
as q increases from 1/2 to 1. Stated another way, if  there exists an equilibrium 1/2 ≤ q ≤ 1.
there exists an equilibrium 1/2 ≤ q ≤ 1.











